Java快速排序和归并排序详解
快速排序
概述
快速排序算法借鉴的是二叉树前序遍历的思想，最终对数组进行排序。
优点：
对于数据量比较大的数组排序，由于采用的具有二叉树二分的思想，故排序速度比较快
局限
只适用于顺序存储结构的数据排序（数组 ，ArrayList等），不适用于链式的数据结构
算法实现思路
一.将目标数组转化为这样一个数组。数组中的某个位置左边的所有数据都比该位置的数据小，该位置右边的数据都比该位置数据大。
实现思路：
1.取出数组第0个数据
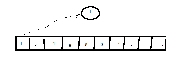
2.从数组最右边开始遍历，如果遍历位置的数据比第0个位置的数据小，将该位置的数据赋值给左边指针停留下的位置。
3.改变遍历方向，从左边开始开始遍历，如果发现左边的数据比第0个位置的数据大，将该位置的数据赋值给2步骤停留下来的位置，并变换方向。
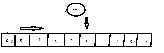
4.循环2、3步骤直到左右遍历到的下标重合
5.将取出的第0个位置的值赋值给循环结束后左右指针停留下的位置
二. 借鉴前序遍历的思路，递归，最终完成排序。
代码实现
private void quickSort(int[] array, int start, int end) {
if (start >= end) {
return;
}
int key = array[start];
int left = start;
int right = end;
boolean direction = true;
L1:
while (left < right) {
if (direction) {
for (int i = right; i > left; i--) {
if (array[i] < key) {
array[left++] = array[i];
right = i;
direction = !direction;
continue L1;
}
}
right = left;
} else {
for (int i = left; i < right; i++) {
if (array[i] > key) {
array[right--] = array[i];
left = i;
direction = !direction;
continue L1;
}
}
left = right;
}
}
array[left] = key;
quickSort(array, start, left - 1);
quickSort(array, left + 1, end);
}
结果测试
@Test
public void testQuickSort() {
int[] array = new int[]{1, 3, 4, 10, 2, 5, 6, 9, 7, 8};
quickSort(array, 0, array.length - 1);
for (int i = 0; i < array.length; i++) {
System.out.println(array[i]);
}
}
结果打印
1
2
3
4
5
6
7
8
9
10
归并排序
概述
归并排序与快速排序相同，同样是借鉴二叉树的思想，时间复杂度O(n),与快速排序一样是大量数据排序的最优方式之一。
思路分析
归并排序是将目标数组分成左右两个数组，左右两个数组必须是有序的，然后对这两个数组合并从而实现排序。对于任意的数组都可以将所有的数据分成若干个数组，每个数组中都只有一个元素，然后两两合并。（因此，归并排序的内存开销会比快速排序多）
代码实现
private void mergeSort(int[] array, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) >> 1;
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
merge(array, left, mid + 1, right);
}
private void merge(int[] array, int left, int mid, int right) {
int leftSize = mid - left;
int rightSize = right - mid + 1;
int[] leftArray = new int[leftSize];
int[] rightArray = new int[rightSize];
System.arraycopy(array, left, leftArray, 0, leftSize);
System.arraycopy(array, mid, rightArray, 0, rightSize);
int index=left;
int leftIndex = 0;
int rightIndex = 0;
while (leftIndex<leftSize&&rightIndex<rightSize){
if(leftArray[leftIndex]<rightArray[rightIndex]){
array[index++] = leftArray[leftIndex++];
}else {
array[index++] = rightArray[rightIndex++];
}
}
while (leftIndex<leftSize){
array[index++] = leftArray[leftIndex++];
}
while (rightIndex<rightSize){
array[index++] = rightArray[rightIndex++];
}
}
测试代码
@Test
public void testMergeSort() {
int[] array = new int[]{1, 3, 4, 10, 2, 5, 6, 9, 7, 8};
mergeSort(array, 0, array.length - 1);
for (int i = 0; i < array.length; i++) {
System.out.println(array[i]);
}
}
结果打印
2
4
6
8
10
Linux公社的RSS地址 ： https://www.linuxidc.com/rssFeed.aspx
本文永久更新链接地址： https://www.linuxidc.com/Linux/2019-08/160014.htm
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
