纯数据结构Java实现(4/11)(BST)

个人感觉，BST(二叉查找树)应该是众多常见树的爸爸，而不是弟弟，尽管 相比较而言 ，它比较简单。

二叉树基础

理论定义，代码定义，满，完全等定义

不同于线性结构，树结构用于存储的话，通常操作效率更高。就拿现在说的二叉搜索树(排序树)来说，如果每次操作之后会让剩余的数据集减少一半，这不是太美妙了么？(当然不当的运用树结构存储，也会导致从 O(logN) 退化到 O(n))。

• 值得说明，O(logN) 其实并不准确，准确来说应该说 O(树的高度)

定义&性质&行话

树里面常见的二叉树: BST, AVL，特殊的AVL(比如2-3树，即红黑树)。

不常见的有(包括多叉树): 线段树，Trie。(但我们说的不常见，不见得真的不常见，可能内核或者框架里面有用到，而写应用的没有用到；所以 常见或者不常见是没有一个确定概率基准的 ，个人把一般写应用的标准定义为基准)

二叉树就是一个最多: 一个爸爸，俩孩子 的树。

这样说，不形象，那形象点儿，直接上代码:

class Node {
    E e;
    Node left;
    Node right;
}

当然，理论教科书上肯定不会这么傻帽的直接告诉你具体情况，它要绕一下，先来一个递归定义，把你绕晕，有图有真相:

然后一个节点也是树，空(null) 也是树。

这里有一些行话，包括上面的认为 logN 就是树高(在一般性的时间复杂度分析时)，解释:

• 深度为 n 的二叉树，每层最多有 2^(n-1) 个节点
• 深度为 n 的二叉树，总共元素，最多有 2^n -1 个节点

(深度从 1 开始，从上往下看)(自己画一下图，脑海中想一下就知道了)

其他行话，满二叉树，完全二叉树，尤其完全二叉树这个概念，后续树结构中有很重要的意义。

• 满的很好理解吧，图上理解，就是所有父亲都有俩孩子；数据上就是元素总共为 2^n-1
• 完全二叉树: 如果你从上到下，从左到右给树的节点编号，那么树应该是你看到的方向排布。

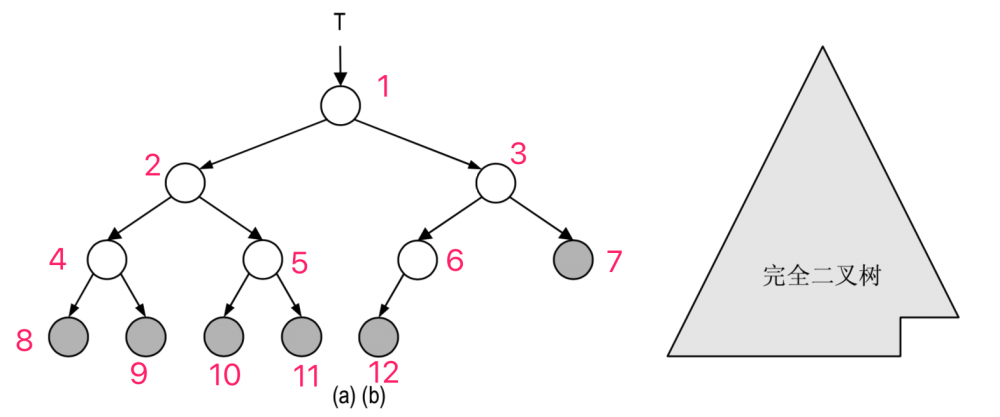
设二叉树的深度为h，除第 h 层(最后一层)外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

个人经验，直接看最后一层是否靠左。

BST基础

BST 说白了也是一种查找树，只是它的存储是有序的。

• (删除的时候要调整，就知道维护的代价了)

存入的值要么是可比较的，要么不能自身提供比较方法时，要主动传入比较器(Comparator)

也就是说，任意一个节点(它作为根节点看待)，它的左子树的值都比它要小，右子树的值都比它大。（正是因为其存储的时候就有序，所以取的时候也高效）

哦，BST 和满二叉树没啥关系。

BST实现

基本框架

先设置好 节点信息 ，大概如下:

package bst;

//二分搜索树
public class BST<E extends  Comparable<E>> {

    //声明节点类
    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    //成员变量
    private Node root;
    private int size;

    //构造函数
    public BST() {
        root = null;
        size = 0;
    }

    public int getSize() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

}

清晰，简介，然后来补充增删查改，遍历等方法。

先做一个规定，对于重复元素的处理是: do nothing。

(它已经在树上了，就不要动了；或者你可以给 Node 增加一个属性 count，专门记录)

增加操作

想象一下，放一个元素到树上，从根节点开始比较，以后的比较也是根据当前树的根元素，从而决定放在左子树，还是右子树上。(上面已经说了，相等的元素，什么也不干)

上面的分析其实已经很清楚了，那么下面考虑一下写法:

• 递归怎么写: 每次切换当前 root 元素，即要搜索的子树
  • 终结条件(base condition): 找到了相关的位置(null)，然后放入元素，返回以该节点为根的子树给上级树，的左/右孩子接收
  • 子树不为空，且元素值不等，说明不是终极条件，那接着切换子树找啊
• 循环怎么写: 思想类似上面，不断下探的过程改成while循环的解法，即不断递推替换 currNode 为其左或者右子树的根节点(就是孩子啦)
  • 技巧是，在寻找合适位置时，不仅需要记录 curr，还要记录 parent
  • 并且实际插入的时候，还是以 parent，即子树的根为合适位置的依据(这根递归做法不同)

一般教科书上才会介绍循环的写法，大致如下: 《算法-C描述》

OK，我们还是用 递归去写吧，不是偷懒，而是 递归更易于宏观理解 啊傻

递归的写法: 不断的切换每层调用的 root 节点的指向 (相当于切换到子树)

大致写法如下: ( 注意柯里化包裹 -- 柯里化参考阮一峰的博客JS语言部分)

• 上面已经说了优化过的递归终止条件，但是也可以像下面这样没有优化(即还没有判断到底就开始分情况返回) --- 作为思考的中间结果吧 --- 优化的结果看最后面的实现。

//向二分搜索树中添加元素
    private void add(E e) {
        if(root == null) {
            root = new Node(e);
            size++;
        } else {
            //切换当前 root 节点进行递归调用
            add(e, root); //第一次调用时已经确定 root != null 了
        }
    }

    private void add(E e, Node node) {
        //这里的 node 相当于一个子树的 root

        //复杂的递归终止条件        
        if(e.equals(node.e)) {
            //已经存在了，do nothing
            return;
        } else if(e.compareTo(node.e)>0 && node.right == null) {
            //不存在子树的情况
            //右子树为空，直接插入
            node.right = new Node(e);
            size++;
            return;
        } else if(e.compareTo(node.e)<0 && node.left == null) {
            node.left = new Node(e);
            size++;
            return;
        }

        //一般的情况，即存在左或者右子树的情况
        //此时已经判断 right 或者 left 不为 null 了
        if(e.compareTo(node.e)>0) {
            //应该在右子树上找位置
            add(e, node.right);

        } else {
            //在左子树上找位置
            add(e, node.left);
        }
    }

但是 终止条件可以写的更加简单一点 ，即一直找到空位置再说插入的事儿，而不是分情况判断时就作为终止条件:

• 找到那个空位置，就在那个位置插入

此时，可以看到，递归函数 add 也需要修改成有返回值了，然后让这个返回值 和原BST挂接 。(返回以当前节点为根的子树，挂接给上级才对；思想就是: 上级只关心完整的结果!)

//返回插入新节点后BST的根 (每层调用都是如此)
    private Node add(E e, Node root) {
        if (root == null) {
            size++;
            return new Node(e);
        }
        if (e.compareTo(root.e) > 0) {
            //放在右子树
            //因为add 函数返回的就是 插入新节点后BST的根
            root.right = add(e, root.right); 

        } else if (e.compareTo(root.e) < 0) {
            root.left = add(e, root.left);
        }
        //相等的情况？抱歉，啥也做

        return root;
    }

• 这里的症结就在于，给当前root的子树(不管左右哪一个)，插入完成后，都会对当前 root 的左或者右孩子进行重新赋值（后半句是，所以才不关心左右子树空不空）

而递归代码中已经包含了 root == null 的情况，即空BST的情况，所以主调函数可以直接调用 private 的 add，而不必再判断 root 为 null:

//client 调用
    //向二分搜索树中添加元素
    private void add(E e) {
        root = add(e, root);
    }

查询操作

这就相当于二分查找，不断的折半 — 这里判断是否存在即可

也可以分为用递归和非递归的写法，然而递归的写法会简单很多，能写递归也能写循环。

递归的写法

• 不断的更换子树 (以根为子树的依据)

//查询元素是否存在
    public boolean contains(E e) {
        return contains(root, e);
    }

    //以 root 为根的BST中是否存在 e
    private boolean contains(Node root, E e) {
        if(root == null) {
            return false;
        }
        if (e.compareTo(root.e) > 0) {
            //去查右子树
            return contains(root.right, e);
        } else if (e.compareTo(root.e) < 0) {
            return contains(root.left, e);
        }
        //return root.e.compareTo(e) == 0;
        return true;
    }

最后的 root.e.compareTo(e) 没有必要，因为除了 > 和 < 剩下的就是 == 的情况了。

遍历操作(递归)

遍历相对来说还是比较容易的， 这里先说深度优先 。

深度优先: 先序遍历，中序遍历，后序遍历；这些都是相对于根元素来说的。

以 先根遍历 来举个例子:

public void preOrder() {
        preOrder(root);
    }

    private void preOrder(Node root) {
        if(root == null) {
            return;
        }
        System.out.println(root.e);
        preOrder(root.left);
        preOrder(root.right);
    }

到这里可以简单测试一下:

public static void main(String[] args) {
        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for(int num: nums){
            bst.add(num);
        }
        bst.preOrder(); //5 3 2 4 6 8
    }

其他的遍历方式，其实就非常容易改写了。

例如 中根遍历:

//中序遍历
    public void inOrder() {
        inOrder(root);
    }

    private void inOrder(Node root) {
        if (root == null) {
            return;
        }

        inOrder(root.left);
        System.out.println(root.e);
        inOrder(root.right);
    }

//测试输出: 2 3 4 5 6 8  (相当于一个排序结果)

从输出的结果可以看到一个性质， BST的中序遍历结果是一个排序结果 。

例如 后序遍历:

//后序遍历
    public void postOrder() {
        postOrder(root);
    }

    private void postOrder(Node root) {
        if (root == null) {
            return;
        }
        
        postOrder(root.left);
        postOrder(root.right);
        System.out.println(root.e);
    }

先把孩子处理好，再来弄自己的事儿。。。可以联系到内存释放，先释放子窗口的，最后在关闭 main。

遍历操作(非递归)

这里用变量的迭代器换也能写，不过我见过的比较高明的手段，用栈来写。

用栈记录后面需要操作(当前还不需要执行)，当前处理的则出栈(这里运用上，有一些技巧)，我直接说了:

• 每次都出栈当前子树根元素 (打印操作)，然后把它的左右子节点反序放入栈中(反序是因为栈是后入先出的);
• 什么时候结束，树遍历完毕的时候；即栈里没有内容了

可以看下代码实现:

//先序遍历，非递归写法
    public void preOrderNR() {
        Stack<Node> stack = new Stack<>();
        stack.push(root); //开始之前的准备，真正的根入栈
        while (!stack.isEmpty()) {
            Node curr = stack.pop();  //出栈当前的根元素
            System.out.println(curr.e);
            if (curr.right != null) {
                stack.push(curr.right);
            }
            if (curr.left != null) {
                stack.push(curr.left);
            }
        }
    }

开始之前，根元素入栈，保证栈里面有内容，然后第一次检查栈，出栈一个元素，即真正的根元素，先打印它，接着其左右孩子反序入栈。下次循环，后入栈的左子树根出栈，进行左边子树的整个操作，全部完毕后才轮到右子树(的根出栈，然后完成类似结果)。

举一个形象的例子:

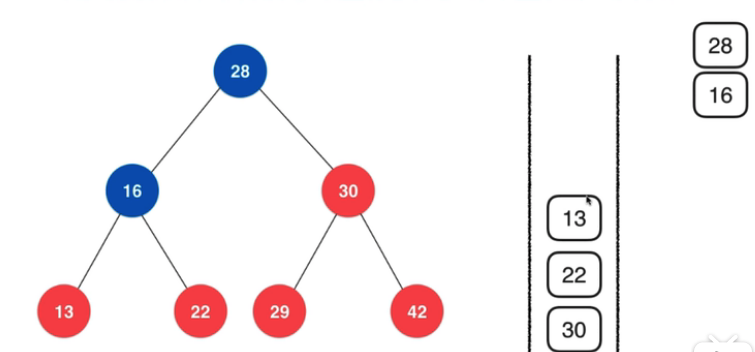
16 出栈后，此时压入 16 的右孩子 22，然后压入左孩子 13。(遍历的反序)

中序遍历，后序遍历的非递归实现？麻烦自己写一下，貌似没有太多实际参考。

层序遍历

就是广度优先啦，这个概念貌似应该用于图，但树也可以用到。

广度优先觉得更应该用于决策，因为它会避免你一条路走到黑。(不至于把一棵子树全部找完，然后发现没找到，才去找另一个子树。。。)

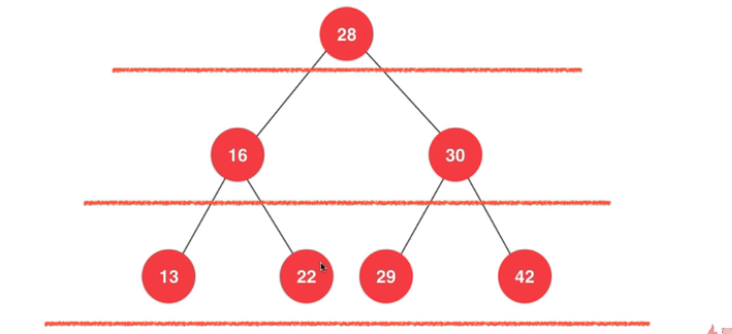
这个我比较熟悉，一般需要借助队列，写非递归实现:

• 每次出队一个元素(当前的根节点)时，把其孩子也先后放入队列中(等待后续遍历)
• 从结果来看，就是层序遍历了 (可以想象一下文件夹的遍历，把当前文件夹的子文件夹放入队列的尾部)

在脑海中可以想象一下，现实司令级别的班子先过，每次检查到一个司令(出队)，就把他手下的军长排在队列的尾部(即所有司令的后部)，这样一直不断，知道司令外部出去，检查第一个军长，同理把他手下的师长全部入队(即所有军长的后面)...直到队列为空，全部遍历完毕。

直接写代码:

//广度优先-层序遍历
    public void levelOrder() {
        Queue<Node> queue = new LinkedList<>(); //util linkedlist 实现了 queue 接口
        queue.add(root);
        while((!queue.isEmpty()) {
            Node curr = queue.remove();
            System.out.println(curr.e);
            if(curr.left != null) {
                queue.add(curr.left);
            }
            if(curr.right != null) {
                queue.add(curr.right);
            }
        }
    }

忘了说了，层序遍历， 先左后右 。

在图中的遍历还需要记录某个节点是否访问过，因为二叉树的爸爸只有一个，但是图中节点的前驱可能有多个的，为避免重复遍历，所以必须标记一下是否访问过。

删除操作(重点)

整个 BST 的难点就在这里，想也知道啊，我删了一个元素，那么以这个元素为根的树怎么调整才能与当前元素的上级挂接(嫁接)好呢？

( 复杂可能在于，需要重新排序树 )

题外话:

我自个儿也是琢磨了一会儿，然后发现对付复杂，**先从特例上找规律，然后推广到一般**。
 
特例的规律如若不能推广到一般，那么就按照第二种思路: 分分合合。
* 分: 详细分析情况，不漏掉情况(暴力穷举)
* 合: 这些具体的，分情况的方案能否合并，上升到一个层级规律

这样的好处，即便不能合，那么分情况的穷举(暴力解法)，我们也能保底。(解决的不优雅，但按性质划分还是属于已解决的分类，有政治优势)

直接说结论，这里采用的是(找到元素)替换(覆盖)要被删除的元素

找一个怎么样的节点去替换啊? 找一个最接近被删除元素大小的元素替换 。

• 此时其实挪动和改变最少，且满足删除后该树仍旧是一棵BST的要求

最接近的元素: 要删除元素的左子树上找最大，要删除元素的右子树上找最小。

先看看一棵子树上怎么找最大最小:(铺垫)

• 查找最小值: 一直寻找左孩子，直到最左边的一个节点 没有左孩子 (null)。
• 查找最大值: 一直寻找右孩子，直到最右边的一个节点 没有右孩子 (null)。

大致实现如下:

//获取树的最小值 (递归写法)
    public E getMin() {
        if(isEmpty()) {
            throw new IllegalArgumentException("Tree is Empty");
        }
        return getMin(root).e;//调用递归的写法
    }

    private Node getMin(Node node) {
        if(node.left == null) {
            return node;
        }
        return getMin(node.left);
    }

    //树的最大值 (非递归写法)
    public E getMax() {
        if(isEmpty()) {
            throw new IllegalArgumentException("Tree is Empty");
        }
        Node curr = root;
        while(curr.right != null) {
            curr = curr.right;
        }
        return curr.e;
    }

这里是拿到值，所以简单，但是删除的话，处理的是 Node，而不仅仅是值。

所以拿到最小元素的节点(当然顺带也要删除这个值)，以及拿到最大元素的节点(顺带也要删除这个值)，这两个值一定是最接近当前元素的，用它们中的一个，来覆盖当前被删除的元素的位置即可。

找到并删除(当前元素相关的)最小元素:

• 最小元素: 向左找没有左节点的最终节点
  • 该节点没有孩子，(左子树一定为空了)，直接删除 —— 叶子节点的情况
  • 该节点有右子树，直接返回该右节点 (作为子树的根，进行下一次循环或者递归起点) —— 非叶子节点
  • 维护 size 的大小

代码实现:

//删除最小值 (递归写法)
    public E removeMin() {
        E ret = getMin(); //不需要 isEmpty判断了
        root = removeMin(root); //操作完毕返回新树的根
        return ret;
    }

    //删除以 node 为根的子树的最小节点；返回该子树的根
    private Node removeMin(Node node){
        //base 情况
        if(node.left == null) {
            //当前子树的左子树为空(不管右子树如何)，说明当前节点最小
            //当然，如果有右子树，要把右子树嫁接到父节点(返回右子树的根给上级即可)

            //删除同时还要把当前节点的孩子置空
            Node rightNode = node.right; //当前节点的左子树可能为空
            node.right = null; //(当前节点的左子树已经为空了)
            size--;
            return rightNode;//返回给上级(具体说，上级的左子树)
        }

        //一般情况 (以 node 为根，还有左子树)
        node.left = removeMin(node.left); //递归过程返回调整后的子树(根节点)
        return node; //每次都返回该子树删除最小值之后的结果
    }

找到并删除(当前元素相关的)最大元素:

此过程类似于删除最小元素，递归操作时，每次都返回删除该node为根的子树的根节点，让上级节点的右节点接收。(末尾节点(右子树一定空)如果没有子节点，即左节点也为空，那么 base 就返回 null，否则把左子树嫁接到上级，具体说就是上级节点的右子树)

代码实现:

//删除最大值 (递归写法)
    public E removeMax() {
        E ret = getMax();
        root = removeMax(root);
        return ret;
    }

    //返回删除最大值后的根节点(子树)给上级节点
    private Node removeMax(Node root) {
        //Base 情况(末尾节点)
        if(root.right == null) { //没右子树了
            //判断其是否还有左子树，然后把左子树返回给上级节点(的右子树接收)
            //同上，不必判断，因为 root.left 即便为 null 也包含在这种情况中
            Node leftNode = root.left;
            root.left = null;
            size--;
            return leftNode;
        }
        root.right = removeMax(root.right);//有右子树那就在右子树上找
        return root;
    }

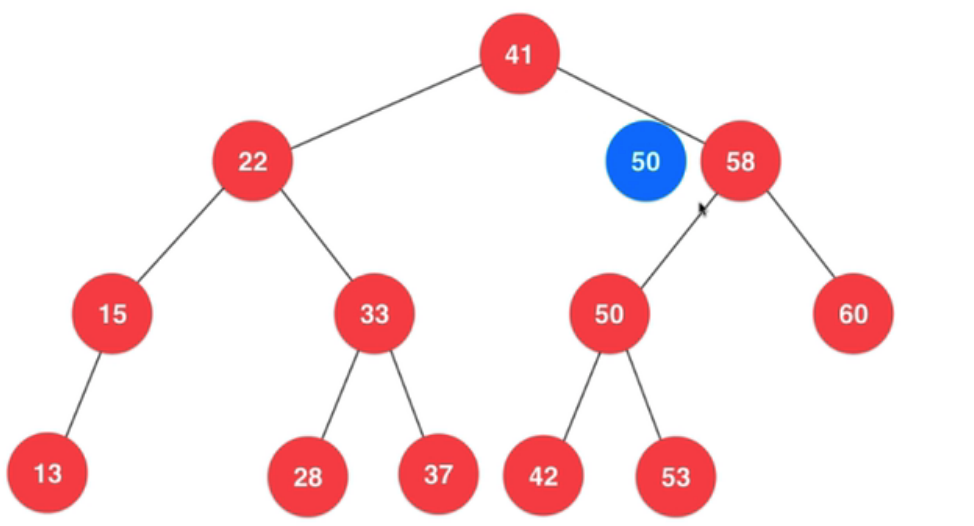
从上面删除最大，最小的逻辑，可以推广到一般情况，具体来说，举个例子:

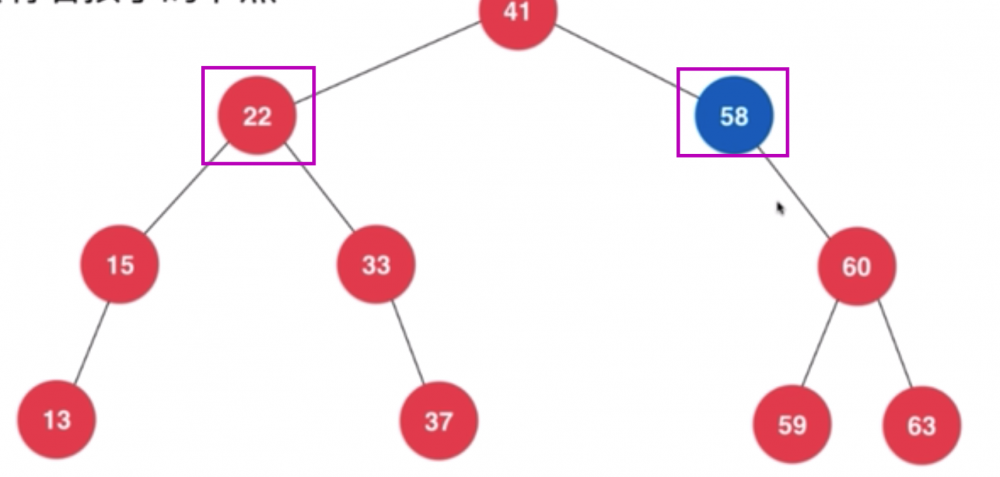
• 删除 58 很容易，直接把 60 这个节点返回给右子树 (因为 41 为根的这棵树已经有左子树)
• 删除 22 则情况至少有两种 (左右都有节点)，一种 15 上位(作为 41 的左子树)，然后 33 接在 15 的右子树上，另外一种则是 33 上位，然后 15 接在 33 的左子树上
  • 这里 22 的子树比较特殊(只有半边子树)，所以可以很容易看出两种情况
  • 也就是说，可以在左边找前驱，也可以在右边找后继
• 叶子节点更简单，不必单独拿出来，直接返回给上级一个 null 即可作为子树即可

若某节点的子树都是满的，则不那么容易，以后继为例，讲一下思路:

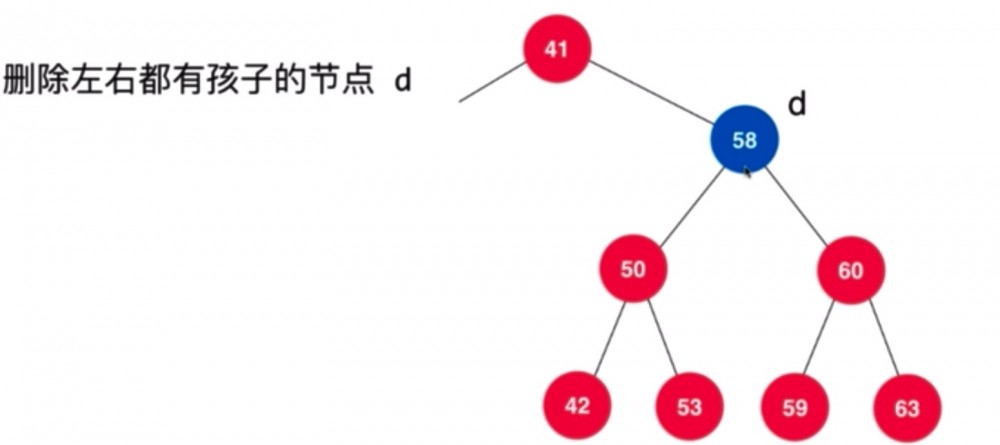
其实就是在右子树上找一个最节点最接近当前值的节点，替代当前要删除的节点。即 min(d->right)。换句话说，右子树中找到最小元素(其实是删除掉这个元素)，然后在 d 的位置填补这个元素，图例如下:

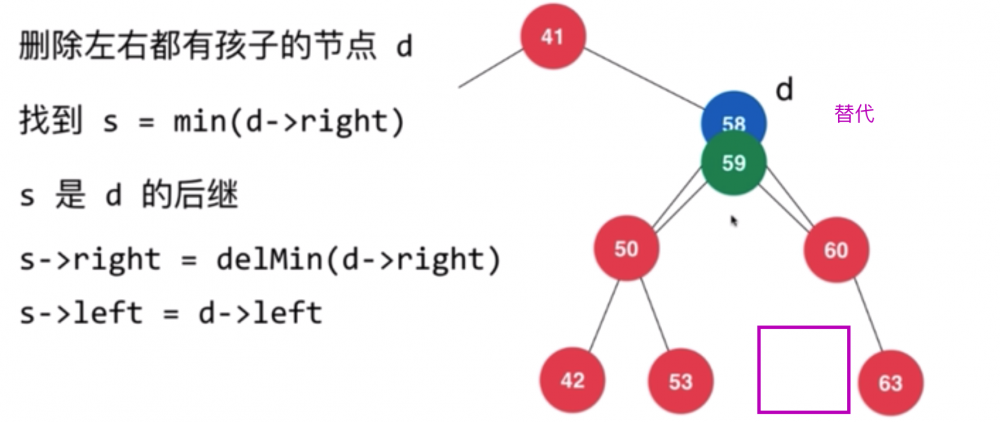
上面把 s 的一切设置好(left, right)，此时 s 就是整个调整完毕的子树根，把它返回给上级树的右子树即可。

这里已经可以看出，结论如下:

• 但凡有一边子树是空的，就是特殊情况，方便处理(下面代码也会证明这一点)
• 整整困难的是两边都是满的，此时需要 找前驱或者后继，替换 这种思路(至于用前驱还是后继，随意; 因为都能保证之后的树是一棵BST)

那么代码实现: (参考删除最大最小的逻辑，推到删除的一般逻辑，以后继为例)

/*找后继的实现*/
    //用户指定删除某个值 e 的节点
    public void remove(E e) {
        root = remove(root, e); //每次递归都是返回操作后的子树(根节点)
    }

    /*
    删除以 root 为根的子树中值为 e 的节点
    返回操作完毕后子树的根
    */
    private Node remove(Node root, E e) {
        //先要找到这个元素

        //base 情况 (前一次递归调用返回的是 null 的情况)
        if (root == null) {
            return null; //这个空值最终会作为上级树的孩子
        }

        //(分情况在子树上找)
        if (e.compareTo(root.e) > 0) {
            //在右子树上找
            root.right = remove(root.right, e);
        } else if (e.compareTo(root.e) < 0) {
            //在左子树上找
            root.left = remove(root.left, e);
        } else { 
            // 找到的情况 e.compareTo(root.e) == 0
            //从其左右子树上找替换元素 (这里采用后继进行替换)
            //同时需要返回新的根节点给上级
            
            /*
            1.左右子树都在 (融合的情况) -- 找到右子树上最小元素进行替代
            2.左子树在，但是没有右子树 (类似于删除最大值的逻辑)
            3.右子树在，但是没有左子树 (类似于删除最小值的逻辑)
            4.左右子树都空了，叶子节点(直接 return null) 即把空子树返回给上级节点(这一种情况已经包含在2, 3的写法中了)
            
            先写 2, 3, 4 这类简单的情况 (返回值接在上层左子树还是右子树不确定，这要看上层的递归调用是哪种情况) 
            */

            if (root.right == null) {
                Node leftNode = root.left;
                root.left = null;
                size--;
                return leftNode; //包含了 leftNode 也为 null 的情况
            }

            if (root.left == null) {
                //类似于查找最小值的情况
                Node rightNode = root.right;
                root.right = null;
                size--;
                return rightNode;
            }

            //左右子树都不空的情况(先找到替代节点 successorNode )
            Node successorNode = getMin(root.right);
            successorNode.right = removeMin(root.right); //返回的是删除最小元素后的根节点
            successorNode.left = root.left;

            //置空原来 root 的 left 和 right
            root.left = root.right = null;
            return successorNode; //返回设置好的元素给上级

        }

        return root;
    }

上面的代码，找到要替换的元素时，分情况分析，即:

1.左右子树都在 (融合的情况) -- 找到右子树上最小元素进行替代

2.左子树在，但是没有右子树 (类似于删除最大值的逻辑) --- 代码类似

3.右子树在，但是没有左子树 (类似于删除最小值的逻辑) --- 代码类似

4.左右子树都空了，叶子节点(直接 return null) 即把空子树返回给上级节点(这一种情况已经包含在2, 3的写法中了)

这相当于在暴力穷举了，然后发现貌似确实不能合并，所以就这样划分了。

BST总结

这里会总一些可能有用的结论:

最重要的一条，BST的有序性(放入其中的元素，有序存储)是有维护代价的

• 遍历：中序遍历，所有元素是升序排列。
• 最大值，最小值: 不断向左找左子树，不断向右找右子树。
• 前驱和后继(节点): 左子树中找最大值就是前驱(predecessor)，右子树中找最小值就是后继(successor)。
• 每个节点Node可以维护额外的属性，比如 count, rank, depth 等，适用于业务查询
• floor 和 ceil: 寻找某个值的 floor 和 ceil
  • 该元素可以不在树上

整个看下来，也就是删除上要仔细考虑好几种情况以及破天荒的有 替换 的思维。

它的实现基本上就先这样(应用上有很多变形，但这与其实现无关，后面再说)。

老规矩，代码请参考 gayhub 。