转载

匈牙利算法（二分图最大匹配问题）

匈牙利算法用于求解无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）问题

二分图

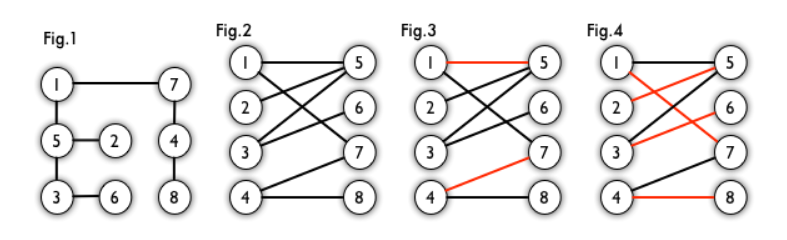
简单来说，有两个点集$U$和$V$ ，集合内部没有边相连，集合之间有边相连，如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

匹配

在图论中，「匹配」（matching）是一个边的集合，其中任意两条边都 没有公共顶点 。例如，图 3、图 4 中红色的边就是图 2 的匹配。

最大匹配

一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

匈牙利算法解决的问题背景：如果一对男女互有好感，那么你就可以把这一对撮合在一起，现在，你拥有的大概就是下面这样一张关系图，每一条连线都表示互有好感。

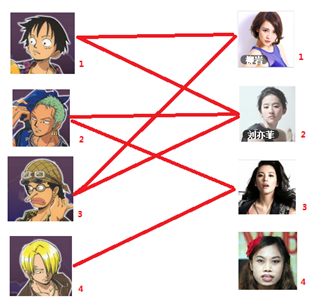
本着救人一命，胜造七级浮屠的原则，你想要尽可能地撮合更多的情侣，匈牙利算法的工作模式会教你这样做：

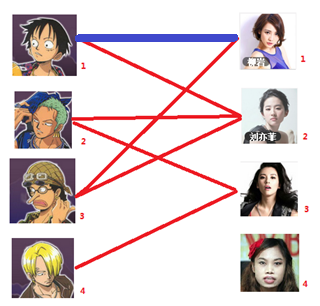
先试着给1号男生找妹子，发现第一个和他相连的1号女生还名花无主，所以！连上一条蓝线
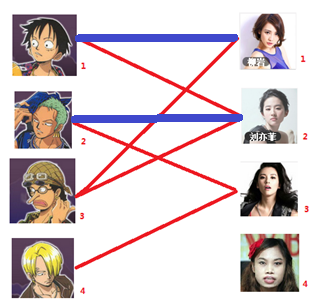
接着给2号男生找妹子，发现第一个和他相连的2号女生名花无主，连上一条蓝线
接下来是3号男生，很遗憾1号女生已经有主了，怎么办呢？我们试着给之前1号女生匹配的男生（也就是1号男生）另外分配一个妹子。(黄色表示这条边被临时拆掉)

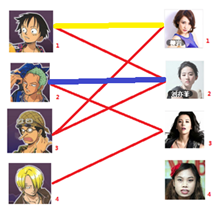
与1号男生相连的第二个女生是2号女生，但是2号女生也有主了，怎么办呢？我们再试着给2号女生的原配，也就是2号男生，重新找个妹子(注意这个步骤和上面是一样的，这是一个递归的过程)

此时发现2号男生还能找到3号女生，那么之前的问题迎刃而解了，回溯回去

2号男生可以找3号妹子

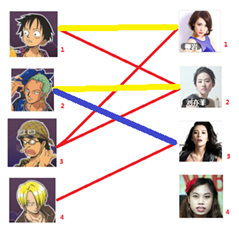
1号男生可以找2号妹子了

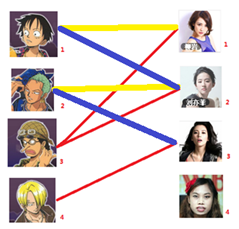
3号男生可以找1号妹子

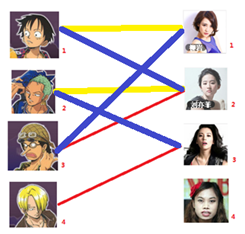
最后是4号男生，很遗憾，按照第三步的节奏没法给4号男生腾出来一个妹子，我们实在是无能为力了。

HDOJ 2063 过山车

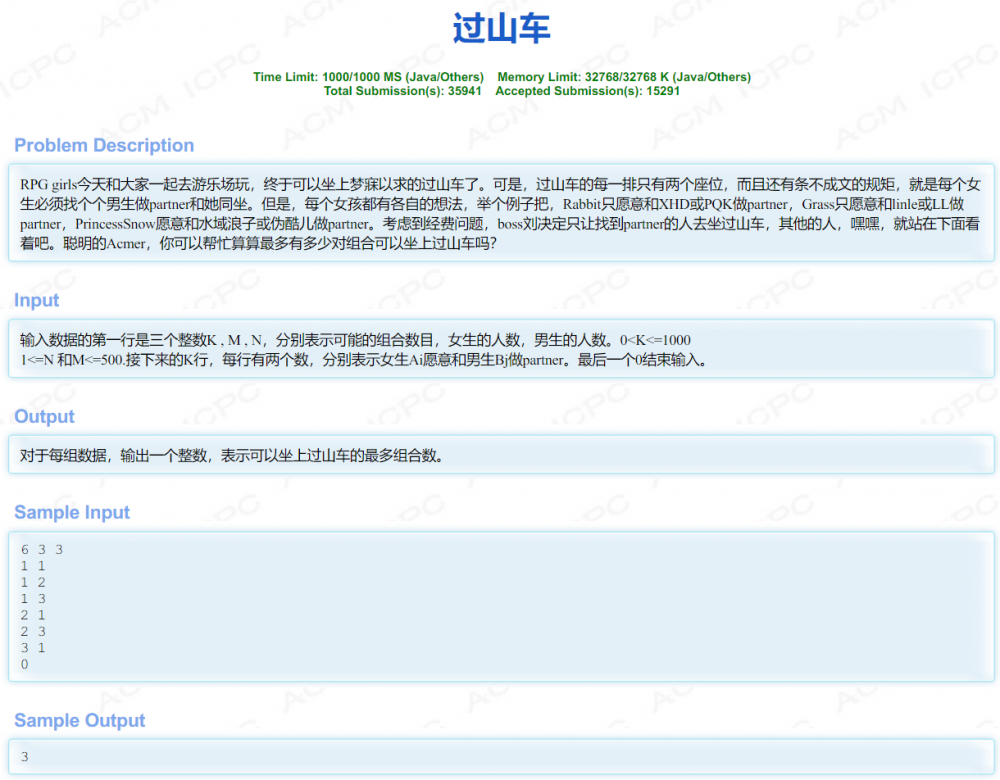匈牙利算法（二分图最大匹配问题）就是一个二分图最大匹配模板题，学完之后立刻巩固一下

import java.util.Arrays;
import java.util.Scanner;

public class Main {
    static int[][] map;
    static int n, m;

    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        while (cin.hasNext()) {
            int t = cin.nextInt();
            if (t == 0)
                break;
            n = cin.nextInt();
            m = cin.nextInt();
            map = new int[n + 1][m + 1];
            for (int i = 0; i < t; i++)
                map[cin.nextInt()][cin.nextInt()] = 1; // 有向边
            int count = 0; // 最大匹配数
            int[] mc = new int[m + 1]; // mc[i] = j 表示i号男生所连的女生是j号
            Arrays.fill(mc, -1); // 初始时所有女生都没有连
            for (int i = 1; i <= n; i++) {
                boolean[] vis = new boolean[m + 1]; // vis[i] = true 表示i号男生已经被匹配了
                if (dfs(i, vis, mc))
                    count++;
            }
            System.out.println(count);
        }
    }

    private static boolean dfs(int start, boolean[] vis, int[] mc) {
        for (int i = 1; i <= m; i++) { // 枚举男生集
            if (!vis[i] && map[start][i] == 1) { // 如果这个男生没被匹配并且和当前的start有边相连
                vis[i] = true; // 将这个男生标记为匹配过
                if (mc[i] == -1 || dfs(mc[i], vis, mc)) { // 这个男生没有和女生匹配 || 这个男生所连的女生还有别的选择，就把这个男生让出来
                    mc[i] = start;
                    return true;
                }
            }
        }
        return false;
    }
}

原文 https://www.wmathor.com/index.php/archives/1344/

正文到此结束