人脸识别技术大总结——Face Detection & Alignment

搞了一年人脸识别，寻思着记录点什么，于是想写这么个系列，介绍人脸识别的四大块：Face detection, alignment, verification and identification(recognization)，本别代表从一张图中识别出人脸位置，把人脸上的特征点定位，人脸校验和人脸识别。（后两者的区别在于，人脸校验是要给你两张脸问你是不是同一个人，人脸识别是给你一张脸和一个库问你这张脸是库里的谁。

人脸检测（detection）在opencv中早就有直接能拿来用的haar分类器，基于Viola-Jones算法。但是毕竟是老掉牙的技术，Precision/Recall曲线渣到不行，在实际工程中根本没法给boss看，作为MSRA脑残粉，这里介绍一种MSRA在14年的最新技术：Joint Cascade Face Detection and Alignment（ECCV14)。这篇文章直接在30ms的时间里把detection和alignment都给做了，PR曲线彪到很高，时效性高，内存占用却非常低，在一些库上虐了Face++和Google Picasa，正好契合这篇想讲的东西。可以作为本节的主线。

人脸校准（alignment）是给你一张脸，你给我找出我需要的特征点的位置，比如鼻子左侧，鼻孔下侧，瞳孔位置，上嘴唇下侧等等点的位置。如果觉得还是不明白，看下图：

图中红色框框就是在做detection，白色点点就是在做alignment。

如果知道了点的位置做一下位置驱动的变形，脸就成正的了，如何驱动变形不是本节的重点，在此省略。

首先介绍一下下面正文要写的东西，由于干货非常多所以可能会看着看着就乱了，所以给出框架图：

=================================

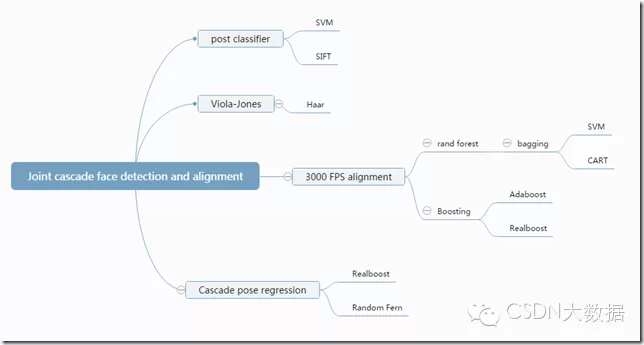
废话说了这么多，正文开始~

detection

作者建立了一个叫post classifier的分类器，方法如下：

1.样本准备：首先作者调用opencv的Viola-Jones分类器，将recal阀值设到99%，这样能够尽可能地检测出所有的脸，但是同时也会有非常多的不是脸的东东被检测出来。于是，检测出来的框框们被分成了两类：是脸和不是脸。这些图片被resize到96*96。

2.特征提取：接下来是特征提取，怎么提取呢？作者采用了三种方法：

第一种：把window划分成6*6个小windows，分别提取SIFT特征，然后连接着36个sift特征向量成为图像的特征。

第二种：先求出一个固定的脸的平均shape（27个特征点的位置，比如眼睛左边，嘴唇右边等等），然后以这27个特征点为中心提取sift特征，然后连接后作为特征。

第三种：用他们组去年的另一个成果Face Alignment at 3000 FPS via Regressing Local Binary Features (CVPR14) ，也就是图中的3000FPS方法，回归出每张脸的shape，然后再以每张脸自己的27个shape points为中心做sift，然后连接得到特征。

3.分类：将上述的三种特征分别扔到线性SVM中做分类，训练出一个能分辨一张图是不是脸的SVM模型。

紧接着作者将以上三种方法做出的分类器和初始分类器进行比对，画了一个样本分布的图：

这个图从左到右依次是原始级联分类器得到的样本分类分布和第一种到第三种方法提取的特征得到的样本分类分布。可见做一下shape alignment可以得到一个更好的分类效果。但是问题来了：如果把所有的windows都做一下alignment，即使是3000 faces per second的速度一张图可能也要处理上1秒，这无法满足一般一秒30帧的实时需求。作者也说，用opencv分类器，参数设成99%的recall率将会带来很严重的效率灾难——一张图能找出来3000个框，处理一张图都要好几秒。

这么渣的效率可咋办呢？以上内容已经证明了alignment确实对detection的preciseness有帮助，这就够啦，对下面的工作也是个启发——能不能在做detection的同时把alignment做了呢？alignment的中间结果是否能给detection带来一些帮助呢？后面慢慢讲。先说两个通用的面部检测和矫正的模型：

1. 级联检测分类器（bagging）：不失一般性，一个简单的级联分类器是这样的：

图中的Ci代表的是第i个弱分类器。x代表的是特征向量，f代表分类得分。每个Ci会根据自己的分类方法对x输出一个分类结果，比如是一张脸或者不是一张脸，而fn（n=1~N)都会对应一个thresholdΘi，让任意一个fn小于对应的Θi的时候，样本就会被拒绝。通常不是一张脸的图片在经过前几个弱分类器的判断后就会被拒绝，根本不用做后面的判断，所以速度很快。

2.级联回归校准（我这翻译…+_+）：这里介绍的是另一个人在10年发的文章：Cascaded Pose Regression (CVPR10)，给图像一个初始shape（通常采用平均shape），然后通过一次一次的回归把shape回归到正确的地方。算法结构很简单，但是效果确实非常好：

回归过程如下：首先提取特征，原作者采用的是Pose-Indexed point features，然后根据特征训练回归函数（可以用线性回归，CART，随机森林等等），原作者采用了一个叫Random Fern Regressor的东西，这里翻译成随机蕨好了（这名字…)，回归出这一阶段的偏移量，然后shape加上这个偏移量，反复这一过程，直到迭代上限或者shape错误率不再下降。随机蕨的算法过程和随机森林类似，他是一个半朴素贝叶斯模型。首先选取M组每组K个特征建立M个蕨（弱分类器），然后假设蕨内特征是相关的，蕨间特征是独立的，这样从统计学上随机蕨是一个完整的把朴素贝叶斯分类器，让计算变得简单：

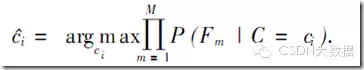
式中C代表分类，ci代表第I类，M代表蕨数量。

综上，这样回归的过程可以总结成如下形式：

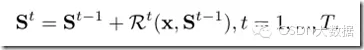
S代表shape，St代表在回归第t阶段的shape，他等于上一阶段的shape加上一个偏置，这个偏置就是上述回归方法之一搞定的。比如随机森林或者随机蕨，或者线性回归。

现在再说说怎么训练得到这个回归Rt。

有两种思路：一种是像刚才随机蕨那样，每个每个蕨的叶子节点存储一个偏移量，计算训练的时候落入这个叶子节点的样本偏移之平均，然后作为最终的叶子节点偏移量。其实就是在优化一个如下目标函数：

然而MSRA组在3000fps中采用的是另一种方法，形状的偏移量ΔδS为：

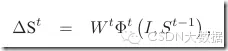
目标函数是：

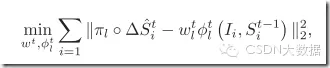
其实也是同样的思路，Φ代表特征提取函数，论文中称Φ的输出为局部二值特征（LBF），W为线性回归参数矩阵，其实就是把提取出来的特征映射到一个二维的偏移量上，是一个2*lenth(特征空间维数)的变换矩阵。

首先讲Φ是怎么训练的：Φ其实就是一个随机森林。输入像素差特征（pixel-difference features），输出一个offest。训练的时候随机给每个根节点像素差特征中的一部分。非叶节点的分裂依据是从输入的pixel-difference features中找出能够做到最大的方差衰减的feature。在最后的叶子节点上写上落在叶子节点上的样本偏移量，这个偏移量在之前说到的fern里有用，但是在这里没啥用，因为作者最后不是用这个做回归的而是用LBF，详细的得往下看。如果有多个样本都落在这里，则求平均。这样训练出来的东西就是下面这个公式所表达的东西：

可能有读者看到这就会不懂了，不用管这个公式，等下面的看完了就会懂了。

但是我只想要其中的Φ，于是这里给出了LBF（local binary feature）的定义，直接简单粗暴地统计所有树叶节点是否被该样本落入，如果落入了就记为1否则记为0，然后把所有的01串连起来就是LBF了。还是看图说话：

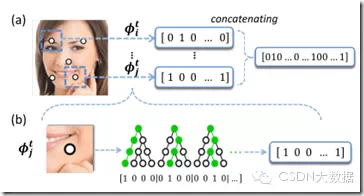
先看b，随机森林的三棵树，样本经过三棵树后分别落在了第1,2,3个叶子节点上，于是三棵树的LBF就是1000,0100,0010.连接起来就是100001000010.然后看a，把27个特征点的lbf都连接起来形成总的LBF就是Φ了。

接下来是训练w：之前已经得到了wΦ（I,S)以及Φ（I,S),现在想求w，这还不容易吗，直接算呀。不过作者又调皮了，他说他不想求w，而是想求一个总的大W=[w1,w2,w3,…,w27].怎么求呢？得做二次回归。至于为什么要这么做下面会介绍。目标函数：

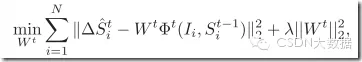
后面加了个L2项，因为W是炒鸡sparse的，防止过拟合。做线性回归即可得到W。

现在解释一下为啥不直接用w1w2w3…而是要再回归出来一个W：原因有两个：

1.再次回归W可以去除原先小wi叶子节点上的噪声，因为随机森林里的决策树都是弱分类器嘛噪声多多滴；

2.大W是全局回归（之前的一个一个小w也就是一个一个特征点单独的回归是local回归），全局回归可以有效地实施一个全局形状约束以减少局部误差以及模糊不清的局部表现。

这样一来，测试的时候每输入一张图片I，先用随机森林Φ求出它的LBF，然后在用W乘一下就得到了下一个stage的shape，然后迭代几次就得到了最终的shape。所以效率十分的快。

好了，兜了一大圈该回来了，刚才讲的是两个uniform的model来做detection和shape regression的。接下来该讲作者是怎么边detection边regression shape的了！

作者建立了一个分类回归树，就叫CRT好了。这个CRT在距离根节点比较近的几层偏重于分类，在接近叶子节点的几层偏重于回归，具体实现上，每个节点究竟用于回归还是分类呢？用一个概率p表示用于分类的概率，自然回归就是1-p了。而这个p随着深数的深度减小，作者采用了一个经验公式：

知道了CRT怎么建立，那就直接就看算法细节吧！边测试是不是脸边做特征点回归的算法如下：

这个模型的训练方法如下：

这样就算完了吗？不，既然要实现，就要细看一下以上用到的各类算法细节：

部分摘自其他博客，详见参考文献。

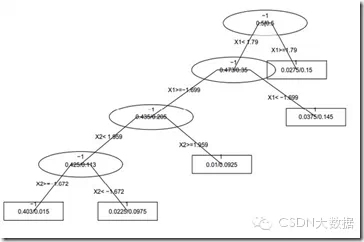
1. CART（Classification And Regression Tree）

思想：递归地将输入空间分割成矩形

优点：可以进行变量选择，可以克服missing data，可以处理混合预测

缺点：不稳定

分类训练过程：

就这样不断分割之后可以建立如下这样的决策树：

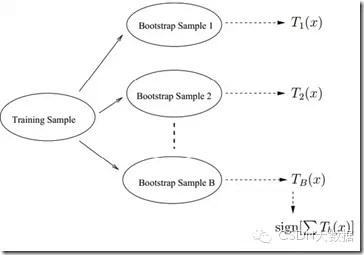
2.Bagging (Breiman1996): 也称bootstrap aggregation

Bagging的策略：

流程图如下：

3.随机森林：

随机森林，指的是利用多棵树对样本进行训练并预测的一种分类器。该分类器最早由Leo Breiman和Adele Cutler提出，并被注册成了商标。简单来说，随机森林就是由多棵CART（Classification And Regression Tree）构成的。对于每棵树，它们使用的训练集是从总的训练集中有放回采样出来的，这意味着，总的训练集中的有些样本可能多次出现在一棵树的训练集中，也可能从未出现在一棵树的训练集中。在训练每棵树的节点时，使用的特征是从所有特征中按照一定比例随机地无放回的抽取的，根据Leo Breiman的建议，假设总的特征数量为M，这个比例可以是sqrt(M),1/2sqrt(M),2sqrt(M)。

因此，随机森林的训练过程可以总结如下：

(1)给定训练集S，测试集T，特征维数F。确定参数：使用到的CART的数量t，每棵树的深度d，每个节点使用到的特征数量f，终止条件：节点上最少样本数s，节点上最少的信息增益m

对于第1-t棵树，i=1-t：

(2)从S中有放回的抽取大小和S一样的训练集S(i)，作为根节点的样本，从根节点开始训练

(3)如果当前节点上达到终止条件，则设置当前节点为叶子节点，如果是分类问题，该叶子节点的预测输出为当前节点样本集合中数量最多的那一类c(j)，概率p为c(j)占当前样本集的比例；如果是回归问题，预测输出为当前节点样本集各个样本值的平均值。然后继续训练其他节点。如果当前节点没有达到终止条件，则从F维特征中无放回的随机选取f维特征。利用这f维特征，寻找分类效果最好的一维特征k及其阈值th，当前节点上样本第k维特征小于th的样本被划分到左节点，其余的被划分到右节点。继续训练其他节点。有关分类效果的评判标准在后面会讲。

(4)重复(2)(3)直到所有节点都训练过了或者被标记为叶子节点。

(5)重复(2),(3),(4)直到所有CART都被训练过。

利用随机森林的预测过程如下：

对于第1-t棵树，i=1-t：

(1)从当前树的根节点开始，根据当前节点的阈值th，判断是进入左节点(<th)还是进入右节点(>=th)，直到到达，某个叶子节点，并输出预测值。

(2)重复执行(1)直到所有t棵树都输出了预测值。如果是分类问题，则输出为所有树中预测概率总和最大的那一个类，即对每个c(j)的p进行累计；如果是回归问题，则输出为所有树的输出的平均值。

注：有关分类效果的评判标准，因为使用的是CART，因此使用的也是CART的平板标准，和C3.0,C4.5都不相同。

对于分类问题（将某个样本划分到某一类），也就是离散变量问题，CART使用Gini值作为评判标准。定义为Gini=1-∑(P(i)*P(i)),P(i)为当前节点上数据集中第i类样本的比例。例如：分为2类，当前节点上有100个样本，属于第一类的样本有70个，属于第二类的样本有30个，则Gini=1-0.7×07-0.3×03=0.42，可以看出，类别分布越平均，Gini值越大，类分布越不均匀，Gini值越小。在寻找最佳的分类特征和阈值时，评判标准为：argmax（Gini-GiniLeft-GiniRight），即寻找最佳的特征f和阈值th，使得当前节点的Gini值减去左子节点的Gini和右子节点的Gini值最大。

对于回归问题，相对更加简单，直接使用argmax(Var-VarLeft-VarRight)作为评判标准，即当前节点训练集的方差Var减去减去左子节点的方差VarLeft和右子节点的方差VarRight值最大。

Random Forest与Bagging的区别在于：Bagging每次生成决策树的时候从全部的属性Attributes里面选择，而Random Forest是随机从全部Attributes的集合里面生成一个大小固定的子集，相对而言需要的计算量更小一些。

4.Boosting(Freund & Schapire 1996):

boosting在选择hyperspace的时候给样本加了一个权值，使得loss function尽量考虑那些分错类的样本（i.e.分错类的样本weight大）。

怎么做的呢？

–boosting重采样的不是样本，而是样本的分布，对于分类正确的样本权值低，分类错误的样本权值高（通常是边界附近的样本），最后的分类器是很多弱分类器的线性叠加（加权组合），分类器相当简单。

结构如图：

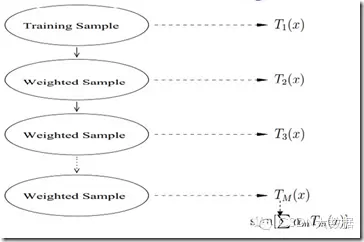
AdaBoost和RealBoost是Boosting的两种实现方法。general的说，Adaboost较好用，RealBoost较准确。由于Boosting算法在解决实际问题时有一个重大的缺陷,即他们都要求事先知道弱分类算法分类正确率的下限,这在实际问题中很难做到。后来Freund和Schapire提出了AdaBoost算法,该算法的效率与Freund方法的效率几乎一样,却可以非常容易地应用到实际问题中。AdaBoost是Boosting算法家族中代表算法,AdaBoost主要是在整个训练集上维护一个分布权值向量D(x)t,用赋予权重的训练集通过弱分类算法产生分类假设Ht(x),即基分类器,然后计算他的错误率,用得到的错误率去更新分布权值向量D(x)t,对错误分类的样本分配更大的权值,正确分类的样本赋予更小的权值。每次更新后用相同的弱分类算法产生新的分类假设,这些分类假设的序列构成多分类器。对这些多分类器用加权的方法进行联合,最后得到决策结果。这种方法不要求产生的单个分类器有高的识别率,即不要求寻找识别率很高的基分类算法,只要产生的基分类器的识别率大于015,就可作为该多分类器序列中的一员。

寻找多个识别率不是很高的弱分类算法比寻找一个识别率很高的强分类算法要容易得多,AdaBoost算法的任务就是完成将容易找到的识别率不高的弱分类算法提升为识别率很高的强分类算法,这也是AdaBoost算法的核心指导思想所在,如果算法完成了这个任务,那么在分类时,只要找到一个比随机猜测略好的弱分类算法,就可以将其提升为强分类算法,而不必直接去找通常情况下很难获得的强分类算法。通过产生多分类器最后联合的方法提升弱分类算法,让他变为强的分类算法,也就是给定一个弱的学习算法和训练集,在训练集的不同子集上,多次调用弱学习算法,最终按加权方式联合多次弱学习算法的预测结果得到最终学习结果。包含以下2点:

样本的权重

AdaBoost通过对样本集的操作来训练产生不同的分类器,他是通过更新分布权值向量来改变样本权重的,也就是提高分错样本的权重,重点对分错样本进行训练。

(1)没有先验知识的情况下,初始的分布应为等概分布,也就是训练集如果有n个样本,每个样本的分布概率为1/n。(2)每次循环后提高错误样本的分布概率,分错的样本在训练集中所占权重增大,使得下一次循环的基分类器能够集中力量对这些错误样本进行判断。

弱分类器的权重

最后的强分类器是通过多个基分类器联合得到的,因此在最后联合时各个基分类器所起的作用对联合结果有很大的影响,因为不同基分类器的识别率不同,他的作用就应该不同,这里通过权值体现他的作用,因此识别率越高的基分类器权重越高,识别率越低的基分类器权重越低。权值计算如下：基分类器的错误率: e = ∑( ht ( x i) ≠yi) Di (1) 基分类器的权重:W t = F( e),由基分类器的错误率计算他的权重。2.3算法流程及伪码描述算法流程描述 算法流程可用结构图 1 描述,如图 1 所示 AdaBoost重复调用弱学习算法(多轮调用产生多个分类器),首轮调用弱学习算法时,按均匀分布从样本集中选取子集作为该次训练集,以后每轮对前一轮训练失败的样本,赋予较大的分布权值( Di 为第i 轮各个样本在样本集中参与训练的概率) ,使其在这一轮训练出现的概率增加,即在后面的训练学习中集中对比较难训练的样本进行学习,从而得到T个弱的基分类器, h1 , h2 , …, ht ,其中 ht 有相应的权值 w t ,并且其权值大小根据该分类器的效果而定。最后的分类器由生成的多个分类器加权联合产生。

（来源：CSDN大数据）

盈利盛宴，交易秘笈——量化投资与高频交易精英班

多名业内顶尖专家齐聚，机会不会再有

真正的高频交易与量化套利培训

实力机构与量化精英相互对接

在资本的培育下助力学员迅速成长

（点击下面的阅读原文查看详情）