【Java】基础篇-排序二叉树
大家好,最近更新的稍微慢了许多,参加了一些公司和外界的技术培训,也跟一些小伙伴聊了些技术文章,总的来说很不理想,讲的内容高大上,落地的过程踩坑很严重,和没听的效果差不多,感觉这几年,圈子太浮躁了,对新技术趋之若鹜,恨不得昨天出来,今天就用到项目上。很值得我反思了。
技术在变,年龄在变,但唯一不变的还是我们的核心技术:Linux、C、TCP/IP这些,不管上层建筑如何变化,都只是在底层基础上封装。
建议大家有选择的去找学习资源,不要当了韭菜,去知识的源头学习,不要尝人家消化过的知识。
在前面的文章中,我们介绍了 Collection 篇 和一篇 HashMap,我们接下来介绍 剩下的 Map 实现,今天我们先来介绍排序二叉树和红黑树,为接下来的 TreeMap 和 TreeSet 做准备,顺便带大家重温一波数据结构。废话不多说,我们正文开始。
排序二叉树
基本概念
二叉查找树(英语:Binary Search Tree),也称为 二叉搜索树 、 有序二叉树 (ordered binary tree)或 排序二叉树 (sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
-
若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
-
若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
-
任意节点的左、右子树也分别为二叉查找树;
-
没有键值相等的节点。 -- <节选自维基百科> img2018.cnblogs.com/blog/102305… )
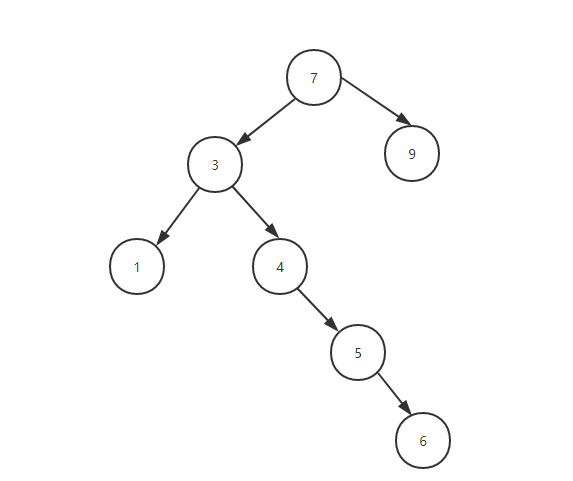
如图,2棵树都是排序二叉树。
运算规则
下面是一个 树的结构:
class Node { /** * 节点 */ Object data; /** * 父节点 */ Node parent; /** * 左子节点 */ Node left; /** * 右子节点 */ Node right; public Node(Object data, Node parent, Node left, Node right) { this.data = data; this.parent = parent; this.left = left; this.right = right; } } 复制代码
查找
排序二叉树有个很好的查找算法,在查找某个元素时,比较高效,当然和数组的下标定位不能比,那是硬件支持的。
- 首先判断树是否空的,如果是空的则查找失败
- 与跟节点进行比较,如果相同,则找到返回
- 如果小于根节点,则递归左子树
- 如果大于跟节点,则递归右子树
private Node getNode(Object e) { Node parent = root; while (parent != null) { //比较父节点元素 和传入的元素 int compareValue = e.compareTo(parent.data); if(compareValue < 0){ //查找左子树 parent = parent.left; } else if(compareValue > 0){ //查找右子树 parent = parent.right; } else{ return parent; } } return null; } 复制代码
插入
向排序二叉树中插入某个元素节点 data 的过程如下:
- 如果 Tree 是空的,则将 data 插入作为根节点
- 如果 data 与跟节点的值相等,则返回
- 如果 data 小于跟节点的值,则在左子树中插入,如果左子树为空,则当前节点为左子树根节点
- 如果 data 大于跟节点的值,则插入右子树插入,如果右子树为空,则当前节点为右子树跟节点
private void insertNode(Object o) { if (root == null) { root = new Node(o, null,null,null); } Node current = root; Node parent = current; int compareValue = 0; while (current != null) { compareValue = o.compareTo(parent.data); // 新节点的值 > parent的值 if(compareValue > 0){ //查找右子树 current = current.right; }else if(compareValue < 0){ //查找左子树 current = current.left; } else { return; } } //创建新节点 Node newNode = new Node(o, parent, null, null); //新节点的值大于 父节点值 if(compareValue > 0){ //设置为右子节点 parent.right = newNode; }else{ //设置为左子节点 parent.left = newNode; } } 复制代码
删除
排序二叉树的删除要稍 微复杂一些:
-
如果要删除的节点为叶子节点
- 直接删除叶子节点即可
Node parent = node.parent;
//要删除的当前节点没有子节点
if (node.left == null && node.right == null) {
if (o.compareTo(parent.data)) {
parent.right = null;
} else {
parent.left = null;
}
}
复制代码
比如 我们删除 0001
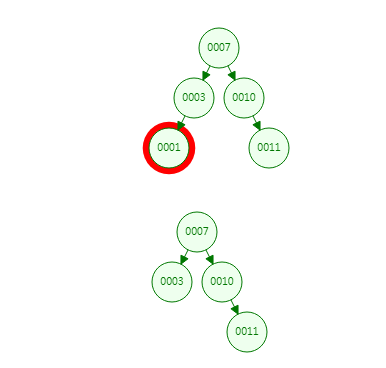
-
节点只有一个孩子节点
- 替换要删除的节点为孩子节点,就跟我们链表的删除类似,子节点与父节点直接关联
//要删除的元素只有一个子节点 //只有一个左节点 if (node.left != null && node.right == null) { //被删除的节点是父节点的左节点 if (node == parent.left) { //父节点的左子节点就是当前节点的左子节点 parent.left = node.left; } node.left.parent = parent; } 复制代码
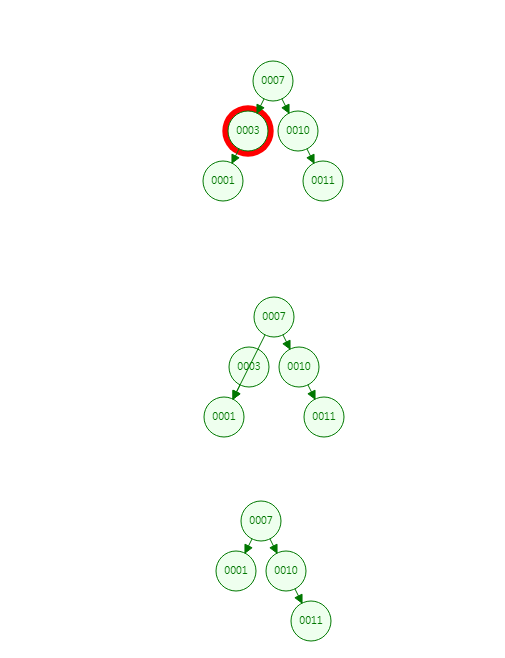
// 只有一个右节点 else if (node.left == null && node.right != null) { if (node == parent.right) { parent.right = node.right; } node.right.parent = node.right; } 复制代码
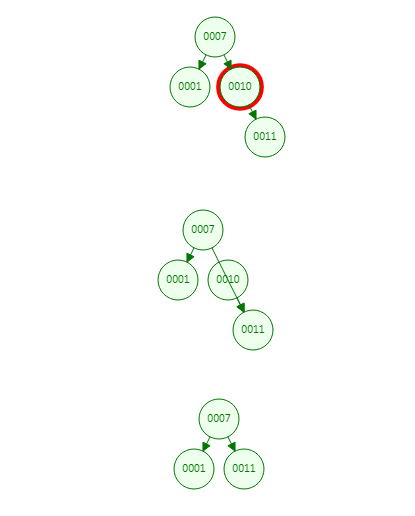
-
节点有两个孩子节点
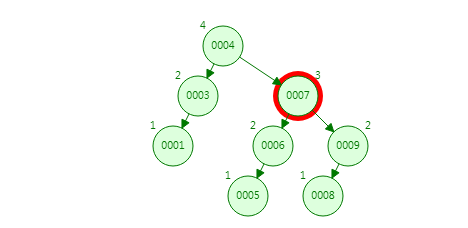
-
寻找到待删除节点的后继节点,把当前节点的内容替换为后继节点的内容,删除后继节点。
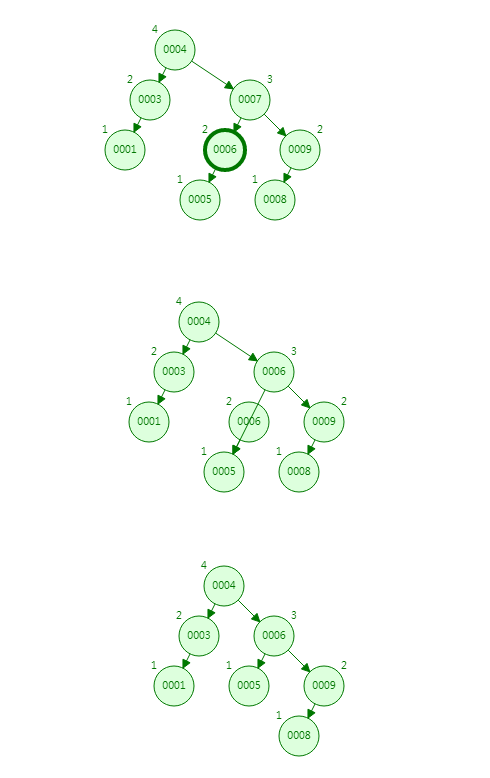
-
后继节点没有左孩子的话,就把两个孩子节点替换为了叶子节点或者说是只有一个孩子节点的情况。
//要删除的元素有 2 个子节点 if (node.left != null && node.right != null) { Node leftMaxNode = node.left; //查找后继节点(注意,这里的后继节点不是左子节点或者右子节点,而是最大节点) while(leftMaxNode.right != null){ leftMaxNode = leftMaxNode.right; } //找到的后继节点与当前待删除的节点进行替换 leftMaxNode.parent = node.parent; //把原来的后继节点删除 leftMaxNode.parent.right = null; if(node == node.parent.left){ node.parent.left = leftMaxNode; } else{ node.parent.right = leftMaxNode; } leftMaxNode.left = node.left; leftMaxNode.right = node.right; node.parent = node.left = node.right = null; } 复制代码
-
上面我们讲的都是高度平衡的排序二叉树:
平衡定义:任何节点的左右子树的高度差最多为一。
但是也有一种极端情况,二叉树直接退化成链表了。比如:
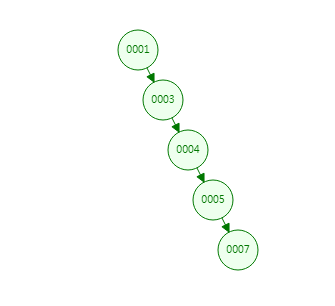
就算没有退化成链表,排序二叉树如果高度不平衡的情况下,效率也会低。
而平衡的排序二叉树又被大家成为 AVL 树,根据它的作者 G.M.Adelson-Velsky 、E.M.Landis 的名字命名的。AVL 算法在插入和删除节点时,会根据一次或者是多次旋转来重新平衡树。当然我们这篇的例子没有写重要的保持平衡算法,只是给大家先回忆一下。之后会在专门的数据结构篇给大家讲解。
红黑树
我们下篇讲的 TreeMap 就是使用的红黑树。红黑树(Red–black tree)与 AVL 树类似,是一种自平衡的二叉查找树,插入和删除节点是通过选择操作来平衡的,不过它不是高度平衡的,而是大致平衡。比如
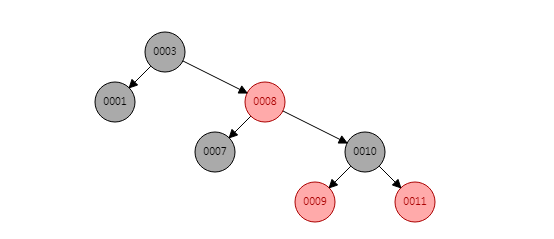
红黑树有如下性质:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
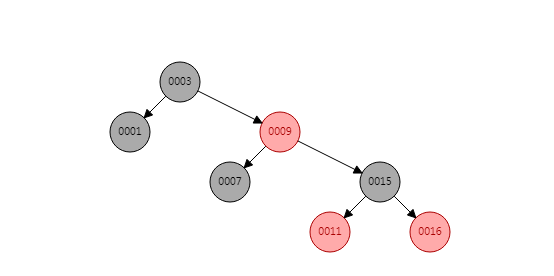
红黑树确保任意一条从跟到叶子节点的路径,没有任何一条的长度比其他路径长过两倍。
比如,最短路径 3 -> 1 的是 2
最长路径3 -> 9 -> 15 ->16 的是4 。正好是2倍。
染色 & 旋转
我们这里只说下红黑树的核心-旋转操作
还是如图
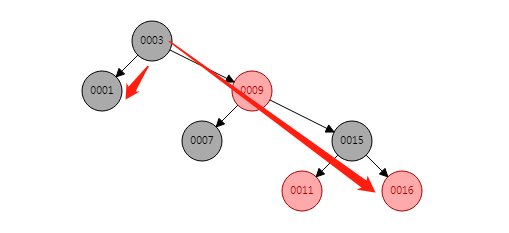
这时,我们插入 20
-
先插入到最大右子树中,并进行染色
- 20 是红色是因为如果设为黑色,就会导致根到叶子的路径上有一条路上,多一个额外的黑节点,这个是很难调整的。但是设为红色节点后,可能会导致出现两个连续红色节点的冲突,那么可以通过颜色调换(color flips)和树旋转来调整
- 这时 20 的父节点 16 和 叔父节点 11 都是红色,这时我们可以把他们进行染色成黑色,并重新染色祖父节点 15 红色

- 这时,11 和 16 的父节点 15 是红色,并且祖父节点 9 也是红色,这时我们就可以通过一次左旋进行跳转
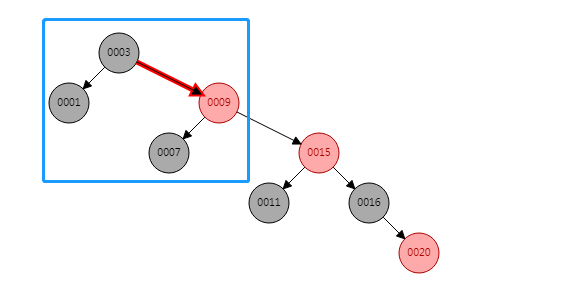
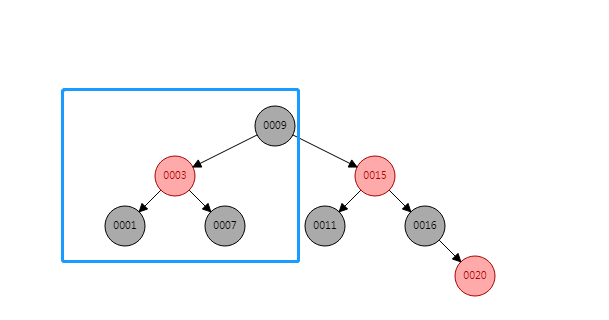
上面我们提到了树的旋转。我们下面再提下相关概念
- 左旋转
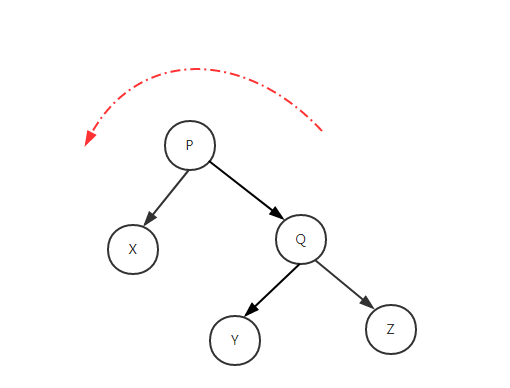
例子:
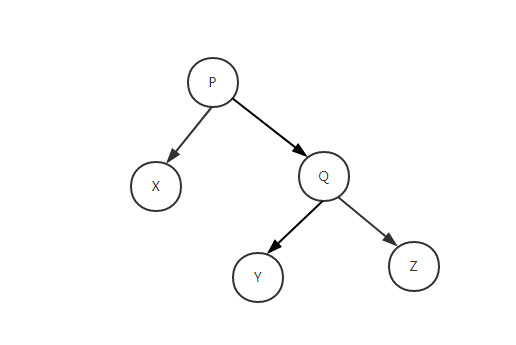
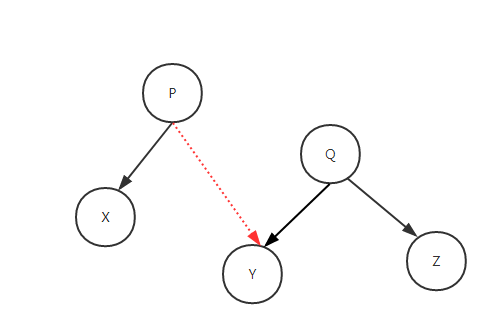
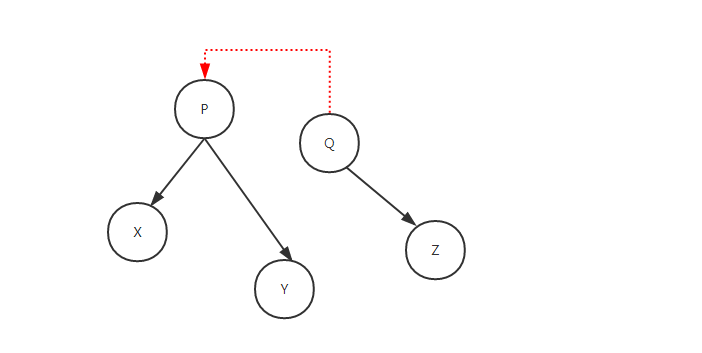
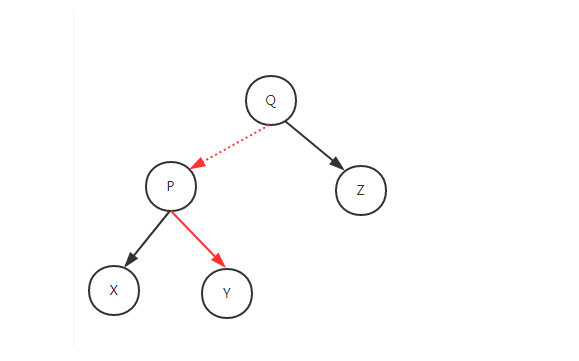
- 右旋转
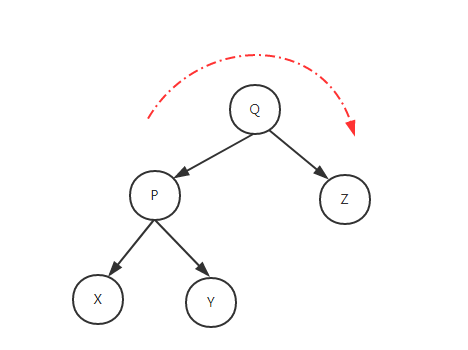
例子:
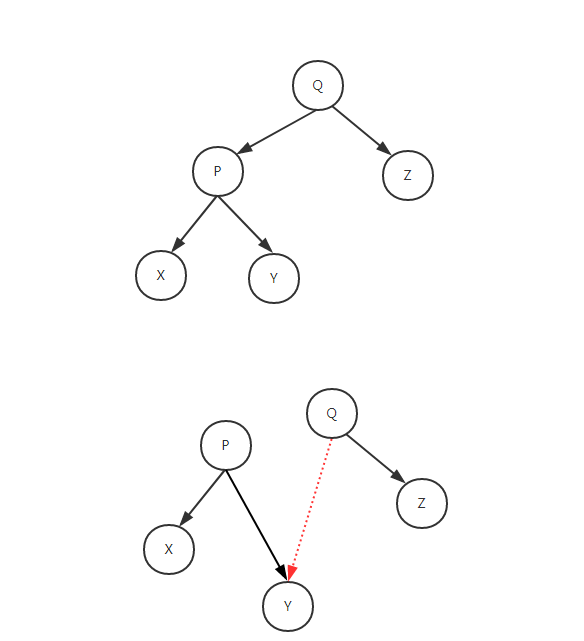
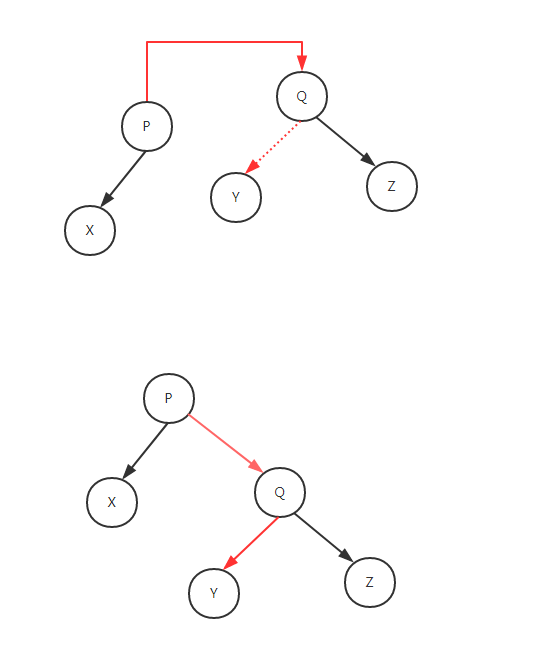











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

