第五届中间件性能挑战赛-冠军队伍攻略分享

0. 公开代码
git clone https://code.aliyun.com/zhangboyang/adaptive-loadbalance.git
git clone https://code.aliyun.com/zhangboyang/mqrace2019.git
1. 初赛: 自适应负载均衡的设计实现
1.1 题目简介
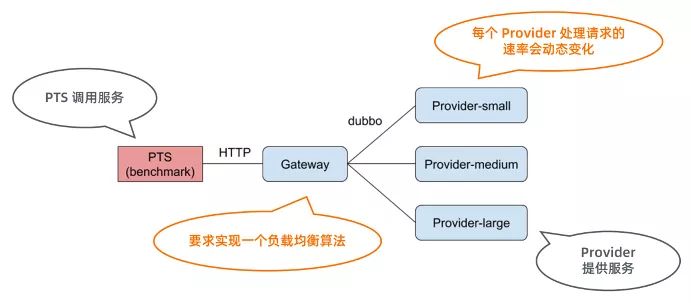
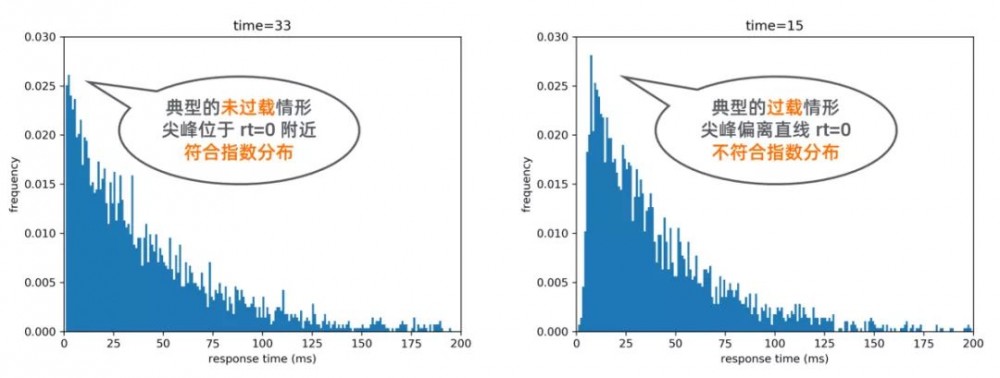
1.2 解题思路
2. 复赛: 实现一个进程内基于队列的消息持久化存储引擎
2.1 题目简介
long t
、
long a
、
char[34] body
;
其中,t 的含义为时间戳数据,a 和 body 为业务数据。
该存储引擎需要实现三个操作:
存储消息
put()
、查询消息
getMessage()
、查询均值
getAvgValue()
。
评测流程也相应地分成三个阶段,每个阶段内部只进行单一的一种操作。
2.2 解题思路
key=(t,a) value=body
,那么查询范围可以用平面上的矩形来表示。
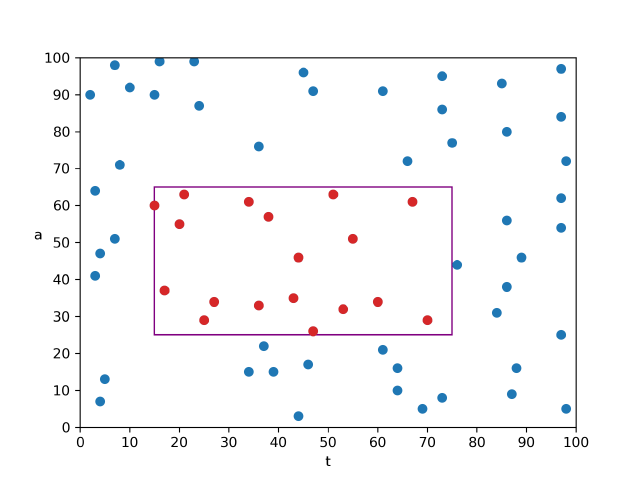 分析要实现的三个操作可以发现:
查询消息一定会访问到所有被查到的消息,性能提升空间存在天花板;
而查询聚合结果则可以通过提前索引等操作避免访问所有被查消息,性能提升空间更大。
因此我们将优化重点放在第三阶段。
为此,我们选择尽量把数据处理操作移到第二阶段,利用第二阶段初始化的时间,整理数据并为第三阶段的查询建立索引。
分析要实现的三个操作可以发现:
查询消息一定会访问到所有被查到的消息,性能提升空间存在天花板;
而查询聚合结果则可以通过提前索引等操作避免访问所有被查消息,性能提升空间更大。
因此我们将优化重点放在第三阶段。
为此,我们选择尽量把数据处理操作移到第二阶段,利用第二阶段初始化的时间,整理数据并为第三阶段的查询建立索引。
put()
操作,我们分析了性能的瓶颈主要在于磁盘的连续 I/O 速度,然而 CPU 资源也十分紧张。
为了提高写入的性能,我们一方面需要尽量减少磁盘 I/O 的字节数,另一方面需要减少 CPU 的开销。
我们设计了一个通用的数值压缩器(
util.ValueCompressor
类),它模仿了 UTF-8 对数值进行变长编码的方式,可以将
long
范围内的整数压缩为 1~9 字节。
数值的前导 0 越多,压缩的效率就越高。
threadXXXX.zp.data
和
threadXXXX.body.data
两个文件(其中
XXXX
为线程 ID 号)。
threadXXXX.zp.data
文件存储的是经过数值压缩器压缩的
(deltaT, a)
数对,由于我们只存储每一条数据中 t 相对上一条数据的 t 的差值,因此在绝大多数情况下,每条记录中 t 的存储只需 1 字节,而 a 根据数据范围的不同会占用不同的字节数,对于 48bit 左右的 a 值,需要 7 个字节进行存储。
threadXXXX.body.data
文件中存储的是完整的未经过处理的 body 数据,每条数据需 34 字节。
按这样计算,所有线程写入磁盘量大约为 84GB,我们在一阶段的得分约为 6800 分。
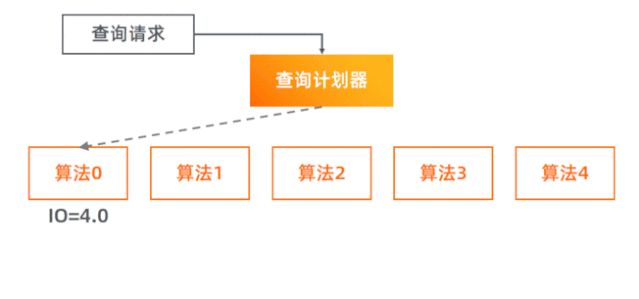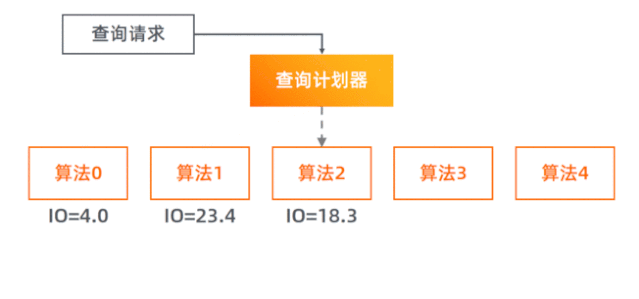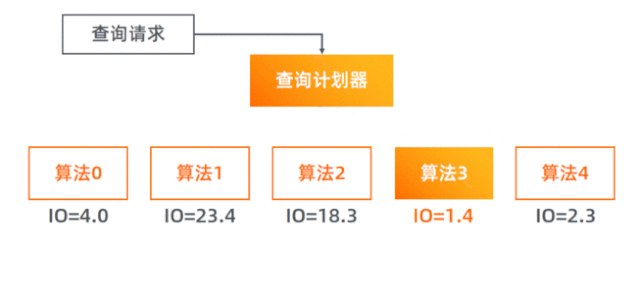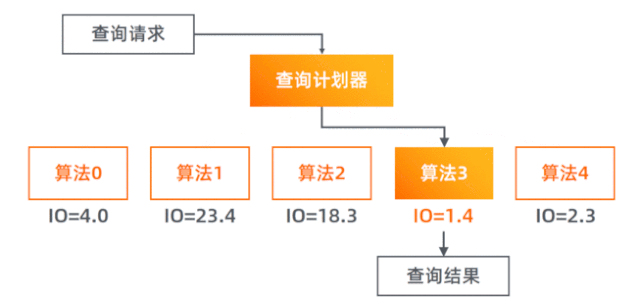
-
算法 0
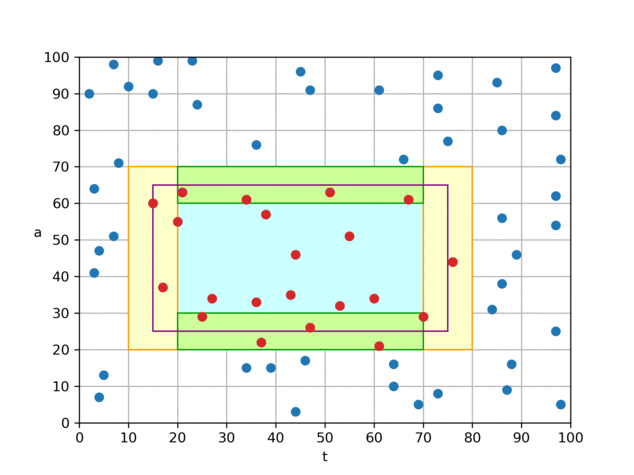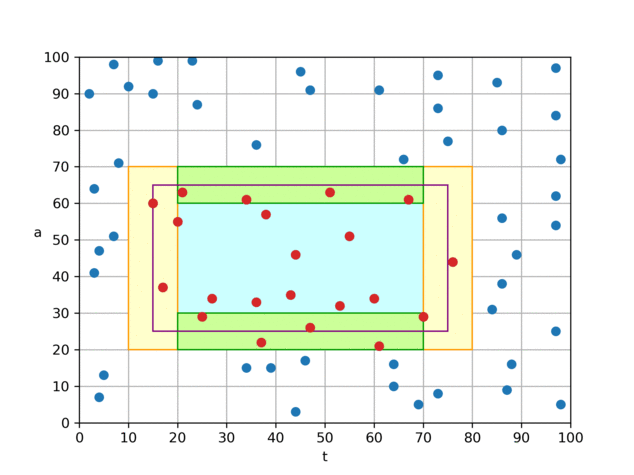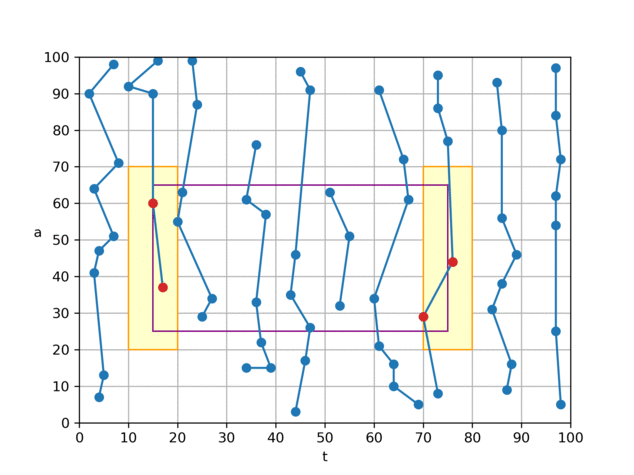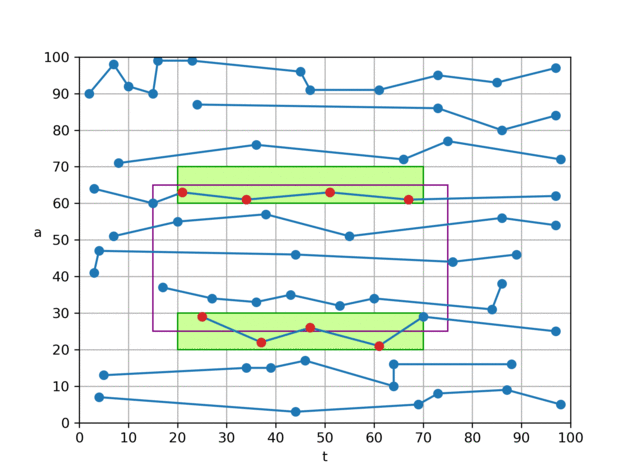
算法 0 是我们认为理论上较为优秀的一个算法。它只会从磁盘中读取与查询矩形四条边相交的块中的数据,对于完全被查询矩形所覆盖到的小块,则由内存中的前缀和可直接计算出“和”、“个数”,无须访问 磁盘, 因此查询的复杂度由 O (查询矩形的面积)降低到 O (查询矩形的边长),相当于从 O(n²) 下降到 O(n) 。
-
具体做法是,对于如图所示的查询矩形,我们将左、右两个 t 分片(黄色)中的
(t,a)数据从磁盘取出并暴力判断,若在查询区域内,则加到结果中; 对于上、下两个夹在 t 分片中间的 a 分片(绿色),根据分片方式,我们可以知晓其 t 一定在查询范围内,因此只需取出 a 数据,并进行判断即可。 为了达到最优 I/O 效率,我们建立了两个文件,一个文件按照 t 方向存储点数据(t,a),另一个文件按照 a 方向,只存储 a 数据,如图中的折线所示。通过这样组织文件,我们可以将 t、a 分片用各自文件的两次连续 I/O 来读取。 这样就可以在 4 次 I/O 代价内,完成平均值的查询。 代码中的实际实现与上文所述略有不同,为了节省空间,我们并未在内存中保留前缀和,而是直接在 a 方向索引文件中保存 a 值在对应 t 分片内的前缀和(文件中只保存前缀和,a 本身的值可通过前缀和来推算),矩形中间的“和”、“数量”便可通过 a 的前缀和、偏移信息推算出来。 另一方面,在内存中我们只保留了一张经过前缀和处理过的“小块内记录数表”(
blockRecordCountPrefixSum数组)。 通过这张表,我们可以在O ( 1 ) 时间内计算每个小块的记录数、每个小块在两个文件中的偏移。 因此,我们的索引实际上只需要在内存中存储一个大小为int[2500000][40]的数组(约占 0.4GB 内存),十分节省内存。虽然算法 0 的效率已经十分优秀,可以在 4 次 I/O 内完成查询,但它的缺点是,不论查询范围是大是小,都需要读取 4 次磁盘。 对于 t 查询范围较小,或 a 查询范围较小的查询,实际上可以用更少的 I/O 次数完成查询。 因此我们针对这类情况设计了其它几个算法。
-
算法 1、算法 2
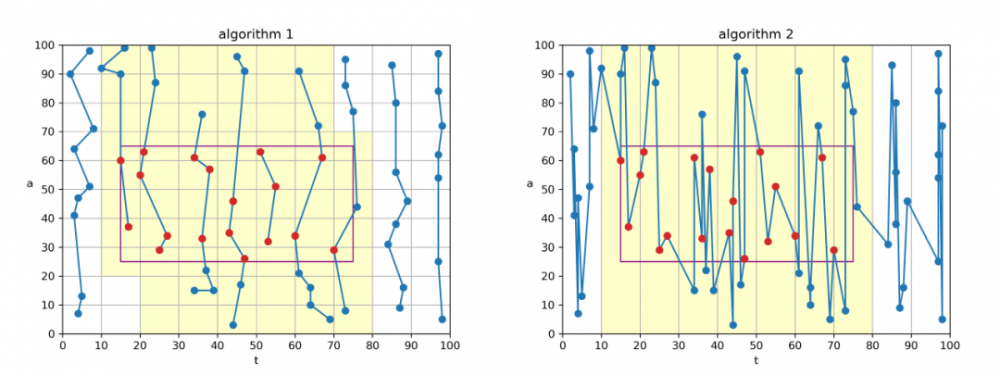
算法 1、算法 2 这两个算法是针对“t 范围小”的查询而设计的。 算法 1 直接采用算法 0 的“t 方向索引”,如果 t 查询范围较少,则可以在 1 次 I/O 之内读取完图中阴影部分的
(t,a)数据(每条为 16 字节),然后进行暴力判断。 算法 2 使用一个单独的索引文件,其内按照 t 方向存储用数值压缩器变长编码的(deltaT,a)数据(每条约 8 字节),然后进行暴力判断。 由于采用了变长编码和 t 差值,为了节省内存,只将分片进行到 t 轴这一层次,不再对 t 轴分片继续划分小块。 因此从数据条数上讲,算法 2 会比算法 1 读入稍多的数据。 不过由于采用了变长编码,从字节数角度讲,算法 2 常常优于算法 1。我们还有一个重要的优化是为算法 2 添加内存缓存。 算法 2 使用到的文件大约为 16GB,我们将其中约 4GB 数据固定于内存中,若读取时命中了内存中的缓存,则直接从内存中取数据,并将 I/O 开销记为 0。 这样可以极大地提高性能。
-
算法 3、算法 4
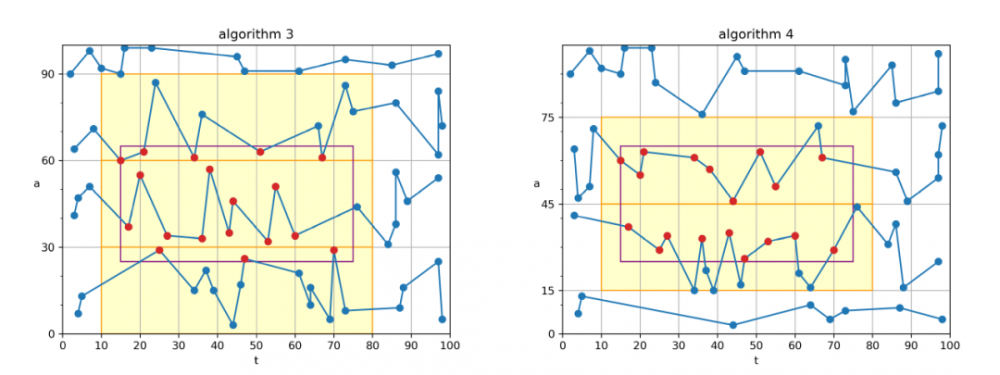
这两个算法是针对“a 范围小”的查询而设计的。 这两个算法代码完全相同,只是 a 轴的划分略有不同。 算法 3 整体采用类似“算法 2”的思路,使用数值压缩器存储
(deltaT,a)数据。 不同的是,存储方向改为 a 轴方向(如左图中的折线所示),而且只对 a 轴分 8 个分片。 通过这样的配置,当 a 查询范围较小时,会落到一个或少数几个分片中,因此可以在一次或少数几个 I/O 内完成查询。 算法 4 与算法 3 采用不同的 a 分片阈值,这样做可以优化“查询矩形恰好跨越边界”这种情况,提高整体的性能。
2.3 一些实现上的细节
-
查询计划器的实现
查询计划器(Query Planner)负责预估各个算法方案的磁盘 I/O 代价并选择最小的那个去执行。 具体的实现是,对于每个算法实现函数,新添加一个参数
boolean doRealQuery,若设置为false,则只查内存中的元数据,计算要读取的字节数,而不进行真正的文件读取及后续处理; 若设为true则进行完整的处理。 查询计划器会先使用doRealQuery=false去调用每一个算法,然后选择 I/O 代价最小的那个,用doRealQuery=true参数去真正执行它。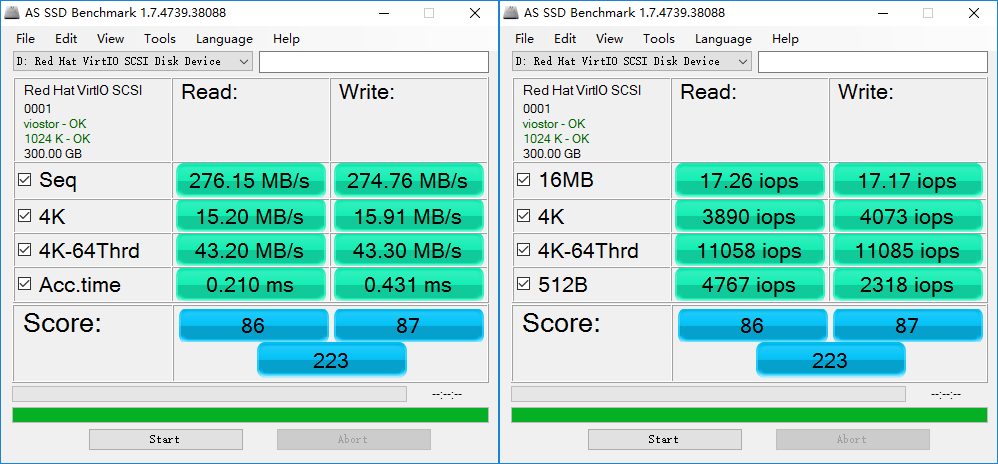
评测机上的 SSD 性能如上图所示。 I/O 代价表现为两个方面: I/O 字节数、I/O 次数。 我们需要一个公式来统一 I/O 代价的计算。 我们选择以 I/O 次数为基准,统一将 I/O 字节数折算为 I/O 次数,具体计算公式如下。 因此一次 I/O 代价最小为 1,最大上不封顶。
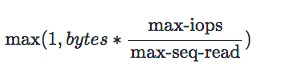
-
一个针对 Java 二维数组的优化
Java 自带的二维数组实际上是“数组套数组”,这样会带来两个问题: (1)如果最右维较小,则对象本身开销占比会很大,浪费内存; (2)如果最左维较大,则会产生很多低维数组对象,给 GC 造成很大压力。 我们自己设计了两个类 Compact2DIntArray 和 Compact2DLongArray。 它们通过使用一维数组来模拟二维数组,既节省内存,也减少 GC 时间。
2.4 代码说明
| 类名 | 功能 |
|
IndexWriter
|
排序、生成索引的代码
|
|
IndexMetadata
|
索引的元数据(如前缀和、文件偏移表等)
|
|
SliceManager
|
分片的元数据(如分片阈值等)
|
|
FileStorageManager
|
文件对象
|
|
CachedCompressedPointAxisT
|
算法 2 的文件缓存
|
|
PutMessageProcessor
|
用于 put() 操作的代码
|
|
GetMessageProcessor
|
用于 getMessage() 操作的代码
|
|
AvgQueryProcessor
|
用于 getAvgValue() 操作的代码
|
util
包内是一些工具代码,详细功能如下表所示:
| 类名 | 功能 |
|
Compact2DIntArray
|
用一维数组模拟二维数组(int)
|
|
Compact2DLongArray
|
用一维数组模拟二维数组(long)
|
|
ValueCompressor
|
数值压缩器,用类似 UTF-8 的方式进行变长编码
|
|
Util
|
其它工具代码(如二分查找等)
|

点击下方图片即可阅读

Apache Flink 零基础入门系列 (六)


如果你在学习过程中,有看到一些比较 优质的文章或Paper,或者你平时自己学习笔记和原创文章,请投稿到天池 ,让更多的人看到。除了精美的 丰富的神秘天池大礼以及粮票奖励 ,更有现金大礼在等着你。
分享成功后你也可以通过下方钉钉群:point_down:主动联系我们的社区运营同学(钉钉号: modestt )

天池宝贝们有任何问题,可在戳“留言”评论或加入钉钉群留言,小天会认真倾听每一个你的建议!














![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

