那些惊艳的 GIS 轮子

一、前言

GIS 涉及测绘、几何拓扑、人文社科等多方面的科学知识。在 .Net 平台下有着许多优秀的开源产品，比如： MapWindow 、 SharpMap 、 WorldWind 等。而在这其中， CoordinateSharp 与 NetTopologySuite 是两款极其令人惊艳的中间开发组件产品。直到最近，我才遇到它们。

真的懊恼早没有人告诉我这些优秀的作品的存在。此前都一直在调用 c/c++的接口，虽说其效率很高，但最终产品还是 .Net 桌面的产品，其间各种相互调用后谁也不能保证效率的优势所在。并且出了问题还得反馈到底层开发组去重新修改编译发布一番。更别说调用 Python 的 shapely 、 geopandas ，或者 Java 的 JTS Topology Suite 、 GeoTools 等。正如聪明的读者想到的那样，可以将业务服务架构在这些优秀的产品之上。为此，有很长一段时间我都在研究 wcf 、 asp.net core 、 Django 、 aspnet-microservices 和 docker 等。的确也出了一些效果和性能均令人满意的服务。但被告知后台业务将由 Java 组的人接手。于是，又开始了 Java 的研究， spring boot 、 spark 、 hbase 等等。也写了一些 Java 的服务端业务。但仍然避免不了高速实时数据处理，并且面向不同终端用户要计算不同需求的问题。最终还是会有一些定制化的业务留在了桌面端。这就像有了云计算后，还需要雾计算、边缘计算作为有益的补充。不可避免的，还得使用 .Net 的实现。

以上都是我用过的各个平台上的优秀产品，没有厚此薄彼的意思。这些也仅仅是为了具体的业务解决问题。下面特别地介绍一下 CoordinateSharp 与 NetTopologySuite 。二者皆是可以跨平台的 .net core 产品。

二、CoordinateSharp

CoordinateSharp 是一个简单易用的进行地理坐标转换、空间天体计算的产品库。其强大与便捷之处我将以几个简单的小列子进行展示，仅抛砖引玉。

1.地理坐标转换

# 北京天安门广场的经纬度
CoordinateSharp.Coordinate.TryParse("N 39° 54' 27/" E 116° 23' 17/"",new DateTime(2019, 10, 1), out var c);
Console.WriteLine($"{c.Latitude.ToDouble()},{c.Longitude.ToDouble()}");//转换结果：39.9075,116.38805555555555

这里有一点令人疑惑的地方就是：为什么会有时间信息。这正是它的独到之处，不仅仅进行坐标转换，还带有计算日、月升落时间，位置等天体信息的能力：

Console.WriteLine($"{c.CelestialInfo.SunRise},{c.CelestialInfo.SunSet}");
# 10/1/2019 10:12:00 PM,10/1/2019 10:00:08 AM

由于时差原因，我们得加上 8 小时（东八区比格林尼治早 8 小时），于是结果变为 10/2/2019 6:12:00 AM,10/1/2019 06:00:08 PM ，日出时间变为第二天的早上了。日出减去 24 小时后为 10/1/2019 6:12:00 AM 。而日落仍然为 10/1/2019 06:00:08 PM 。查阅网上实时的信息：

基本一致，误差的原因由地球是椭球体、自转公转速率缓慢改变等引起。这个差别能够让人接受。

2.空间计算

计算球面距离

// 北京首都机场经纬度
var c1 = new CoordinateSharp.Coordinate(40.0760979329, 116.5953477768);
// 上海虹桥机场经纬度
var c2 = new CoordinateSharp.Coordinate(31.1982791377, 121.3356526703);
var d0 = new CoordinateSharp.Distance(c1, c2);
Console.WriteLine(d0.Kilometers);// 1074.0736250617888
Console.WriteLine(c1.ECEF);// 地球中心地球固定坐标（世界坐标系） -2188.311 km, 4369.881 km, 4084.559 km

而我们在网上查到的信息如下（注意，飞机真实飞行路线并非都是直线）：

上海到北京的空中距离为 1084 公里，上海虹桥机场到首都机场飞行距离为 1160 公里

这与计算结果 1074.0736250617888 接近（没有办法排除各各家数据差异对距离计算结果产生的影响，比如，谷歌、百度、腾讯高德的坐标都不同，上述两个机场的位置坐标就是网上谷歌地球上取得的）。

此外，Coordinate 类有一个极其有用的方法 void Move(double distance, double bearing, Shape shape) 。其作用是计算往某个方向移动某个距离后的新坐标。

// 在椭球上向正北（方位角bearing正北为0）移动十公里,与c1原值比起来，经度基本没有变化
c1.Move(10000,0,Shape.Ellipsoid);
Console.WriteLine($"{c1.Latitude.ToDouble()},{c1.Longitude.ToDouble()}");// 40.16739008225999,116.60039000000003

由此看来，地理空间能力基本上解决了距离与位置的相互转换。更多功能欢迎探索 https://github.com/Tronald/CoordinateSharp 。去 star。

三、NetTopologySuite

NetTopologySuite 是一个快速可靠的 .Net GIS 解决方案。它提供了 JTS Topology Suite 所有功能的直接接口。JTS 是用于建模和平面几何计算，并且遵循 Open GIS 的 SQL 简单特性规范。而 NTS 基本上拥有这些能力，并且 microsoft 用其来为 EF Core （This feature was added in EF Core 2.2.）提供空间计算能力。详情可以参看 Spatial Data 。可以说 JTS 是几何拓扑工具的 Java 实现，而 NTS 是 .NET 下的实现。

1.WKT 读写

var wkt = new WKTReader();
var gm = wkt.Read("POLYGON ((0 0,100 0, 100 100,0 100,0 0))");  //边长为100的正方形
Console.WriteLine(new WKTWriter().Write(gm));// POLYGON ((0 0, 100 0, 100 100, 0 100, 0 0))

2.几何图形计算

// 几何创建工厂（也可不使用工厂模式直接创建几何图形）
var gf = new GeometryFactory();
var pg3 = gf.CreatePolygon(new[]
{
    new Coordinate(612, 612),
    new Coordinate(144, 355),
    new Coordinate(165, 188),
    new Coordinate(277, 328),
    new Coordinate(612, 612)
});
var pg4 = gf.CreatePolygon(new[]
{
    new Coordinate(412, 612),
    new Coordinate(555, 455),
    new Coordinate(655, 188),
    new Coordinate(577, 328),
    new Coordinate(412, 612)
});

绿色是 pg3，金色是 pg4

求并集： var union = pg3.Union(pg4);

求交集： var intersection = pg3.Intersection(pg4);

求差集： var difference = pg3.Difference(pg4);
中间的连线是绘制时导致的，但是计算结果正确。我们查看其 WKT 描述为： MULTIPOLYGON (((478.68239179148486 538.78926215899912, 612 612, 499.14366946688551 516.32478247341942, 478.68239179148486 538.78926215899912)), ((478 498.4, 277 328, 165 188, 144 355, 460.37522887113056 528.73596970059953, 478 498.4))) 的确是两个多边形。

其他能力，比如计算几何间距、面积、凸包、判断是否相交、是否覆盖等可查看项目的介绍或者 test 例子。详情访问 https://github.com/NetTopologySuite/NetTopologySuite 。去 star。

四、CoordinateSharp 与 NetTopologySuite

这么多优秀产品为何单独介绍 CoordinateSharp 与 NetTopologySuite？

假设有需求为画出某一城区的缓冲区，间距为 10km。这可怎么办？

在 NetTopologySuite 中直接提供缓冲区的计算函数 public Geometry Buffer(double distance) ,效果也非常好：

红色为原始直线，按彩虹色依次相距为 10 的缓冲区

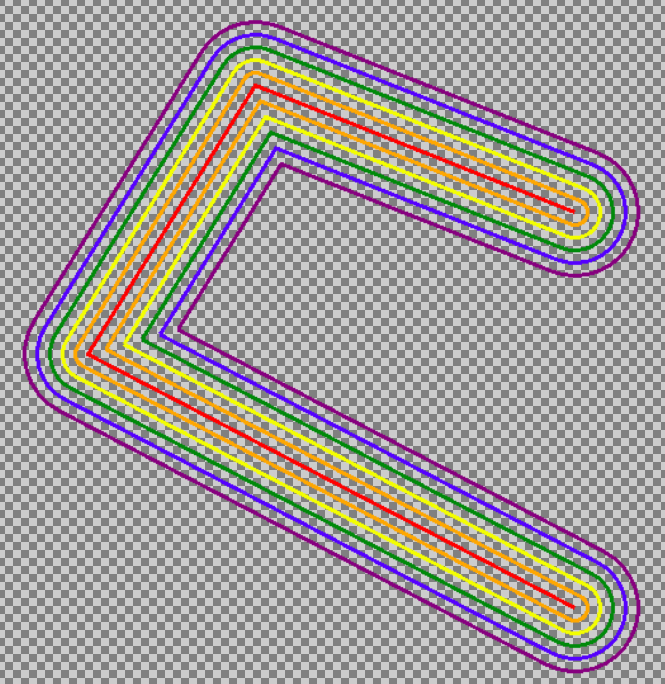
但是我们却忽略了一个重要的事情，NetTopologySuite 的计算的距离为平面坐标系下的欧氏距离。二维平面欧式距离的计算为 Math.Sqrt(Math.Pow(x1-x2,2),Math.Pow(y1-y2,2)) ,直接用经纬度计算首都机场与虹桥机场的二维欧式距离为： 10.06 。而这个值显然对应着球面距离 1074.07 千米。考虑到随着维度的不同，两者之间的比例也并非是定值。最简单的例子就是，在赤道附近，一个经度差对应球面距离为 111.19 千米，而在 80° 纬度上则缩小到 19.31 千米，而在 90° 极点则几乎为 0 千米。

这时，我们就可以利用 CoordinateSharp 中点的移动功能，计算出给定球面距离对应的经纬度，然后利用移动前后的经纬度再计算欧式距离，得出的结果才较为准确。

还是以虹桥机场为例，绘制其半径为 100 千米的缓冲区：

// 对move进行简单的封装
public static double[] ConvertEarthDToPlaneXY(double lat, double lon, double distance, double bearing,
    Shape shape = Shape.Ellipsoid)
{
    var c0 = new CoordinateSharp.Coordinate(lat, lon);
    c0.Move(distance, bearing, shape);
    return new[] { c0.Latitude.ToDouble(), c0.Longitude.ToDouble() };
}

// 虹桥的位置
var hongqiao = new Coordinate(31.1982791377, 121.3356526703);
var hqPoint = gf.CreatePoint(hongqiao);
// 得出正西方向的100千米的位置hqMove
var hqMove = ConvertEarthDToPlaneXY(hongqiao.X, hongqiao.Y,100000, 270);
// 计算移动前后的欧式距离
var hqR = hongqiao.Distance(new Coordinate(hqMove[0], hqMove[1]);
// 计算buffer
var hqCircle = hqPoint.Buffer(hqR);
//验证得出的buffer上的点与虹桥机场的位置
hqCircle
    .Coordinates
    .ToList()
    .ForEach(t =>
    {
        var c1 = new CoordinateSharp.Coordinate(t.X, t.Y);
        var c2 = new CoordinateSharp.Coordinate(31.1982791377, 121.3356526703);
        var d0 = new CoordinateSharp.Distance(c1, c2, Shape.Sphere);
        Console.WriteLine(d0.Kilometers);
    });

验证结果如下：

116.66885608202652
116.05364820797979
114.28764035412392
111.60513634687186
108.37944785253909
105.09000981559511
102.2637861494519
100.38650671049055
99.79581077763879
100.59276661692931
102.61595683755391
105.4929026708211
108.73914573002186
111.85882184494989
114.41831613054764
116.0891677559819
116.66885608202652
116.0891677559819
114.41831613054846
111.85882184495108
108.73914573002347
105.4929026708211
102.61595683755391
100.59276661692915
99.7958107776412
100.38650671049055
102.26378614945223
105.09000981559511
108.37944785253909
111.60513634687305
114.28764035412605
116.05364820797979
116.66885608202652

大部分结果都超过了 100 千米，并且误差超过了 10 千米。比较妥善的方式就是计算多个方向的距离，然后取一个平均值。

public static double AverageDistance(double lat,double lon,double distance,int part)
{
    var seg = 360 / part;
    var rs = new List<double>();
    var raw = new Coordinate(lat, lon);
    for (var i = 0; i < 360; i += seg)
    {
        var move = ConvertEarthDToPlaneXY(lat, lon, distance, i);
        var r = raw.Distance(new Coordinate(move[0], move[1]));
        rs.Add(r);
    }
    return rs.Average();
}

上述缓冲区的距离计算改为：

// 取4个方向（0°、90°、180°和270°）对应的距离，然后求均值
var hqR = AverageDistance(hongqiao.X, hongqiao.Y, 100000,4);

得出的结果如下：

108.4796420377765
107.90879824241405
106.26991268291549
103.77978023046698
100.78401282732902
97.7268731801004
95.09732271673099
93.34698897092896
92.79099574532
93.52530908781738
95.401788528952
98.07519029469032
101.09498625442704
103.9991018274525
106.38288739908288
107.93950641121064
108.4796420377765
107.93950641121104
106.38288739908288
103.9991018274531
101.09498625442863
98.07519029469222
95.40178852895636
93.5253090878196
92.7909957453224
93.34698897093132
95.09732271673535
97.72687318010274
100.78401282733111
103.7797802304676
106.26991268291549
107.90879824241446
108.4796420377765

从结果中可以看出，误差控制在 10 千米之内。

上述计算的是一个点的缓冲区，如果是 LineString 或者 Polygon 的缓冲区，则尽可能的取其上不同的点进行距离转换后求取均值。

五、总结

总的来说，结合 CoordinateSharp 与 NetTopologySuite 可以进行许多有用的计算。但是误差也不可避免，特别是纬度较高的时候。

如果各位有其他更好的解决方案，希望提交评论。