Java8：使用并行流

对于斐波那契数的计算，我们都知道最容易理解的就是递归的方法：

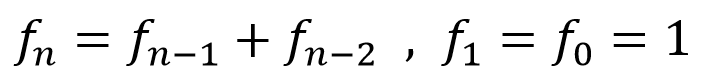
public long recursiveFibonacci(int n) {
    if (n < 2) {
        return 1;
    }

    return recursiveFibonacci(n - 1) + recursiveFibonacci(n - 2);
}

复制代码

当然这个递归也可以转化为迭代：

public long iterativeFibonacci(int n) {
    long n1 = 1, n2 = 1;
    long fi = 2; // n1 + n2

    for (int i = 2; i <= n; i++) {
        fi = n1 + n2;
        n1 = n2;
        n2 = fi;
    }

    return fi;
}
复制代码

但是，对于以上两种方法，并不能并行化，因为后一项的值依赖于前一项，使得算法流程是串行的。所以引出了可以并行的计算斐波那契数的公式：

=>

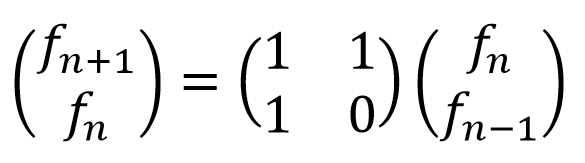
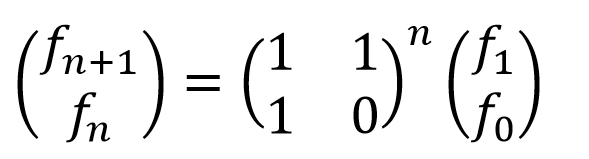
f0 和 f1 都是 1 —— 很明显我们可以对 (1, 1; 1, 0) 进行并行计算。

首先我们定义一个 Matrix 类，用来表示一个 2*2 的矩阵：

public class Matrix {

    /**
     * 左上角的值
     */
    public final BigInteger a;
    /**
     * 右上角的值
     */
    public final BigInteger b;
    /**
     * 左下角的值
     */
    public final BigInteger c;
    /**
     * 右下角的值
     */
    public final BigInteger d;

    public Matrix(int a, int b, int c, int d) {
        this(BigInteger.valueOf(a), BigInteger.valueOf(b),
                BigInteger.valueOf(c), BigInteger.valueOf(d));
    }

    public Matrix(BigInteger a, BigInteger b, BigInteger c, BigInteger d) {
        this.a = a;
        this.b = b;
        this.c = c;
        this.d = d;
    }

    /**
     * multiply
     *
     * @param m multiplier
     * @return
     */
    public Matrix mul(Matrix m) {
        return new Matrix(
                a.multiply(m.a).add(b.multiply(m.c)), // a*a + b*c
                a.multiply(m.b).add(b.multiply(m.d)), // a*b + b*d
                c.multiply(m.a).add(d.multiply(m.c)), // c*a + d*c
                c.multiply(m.b).add(d.multiply(m.d)));// c*b + d*d
    }

    /**
     * power of exponent
     *
     * @param exponent
     * @return
     */
    public Matrix pow(int exponent) {
        Matrix matrix = this.copy();

        for (int i = 1; i < exponent; i++) {
            matrix = matrix.mul(this);
        }

        return matrix;
    }

    public Matrix copy() {
        return new Matrix(a, b, c, d);
    }

}
复制代码

然后我们来比较迭代和并行的效率：

我们先设置并行使用的线程数为 1，即 单线程 。

public static void main(String[] args) throws Exception {
    final int ITEM_NUM = 500000; // 计算斐波那契数列的第 ITEM_NUM 项

    System.out.println("开始迭代计算...");
    long begin = System.nanoTime();

    BigInteger fi1 = iterativeFibonacci(ITEM_NUM);

    long end = System.nanoTime();
    double time = (end - begin) / 1E9;
    System.out.printf("迭代计算用时: %.3f/n/n", time);

    /* ------------------------------ */
    System.out.println("开始并行计算...");
    begin = System.nanoTime();

    BigInteger fi2 = parallelFibonacci(ITEM_NUM, 1);

    end = System.nanoTime();
    time = (end - begin) / 1E9;
    System.out.printf("并行计算用时: %.3f/n/n", time);

    System.out.println("fi1 == fi2：" + (fi1.equals(fi2)));
}

static BigInteger iterativeFibonacci(int n) {
    BigInteger n1 = BigInteger.ONE;
    BigInteger n2 = BigInteger.ONE;
    BigInteger fi = BigInteger.valueOf(2); // n1 + n2

    for (int i = 2; i <= n; i++) {
        fi = n1.add(n2);
        n1 = n2;
        n2 = fi;
    }

    return fi;
}

static BigInteger parallelFibonacci(int itemNum, int threadNum) throws Exception {
    final Matrix matrix = new Matrix(1, 1, 1, 0);
    final Matrix primary = new Matrix(1, 0, 1, 0); // (f0, 0; f1, 0)
    final int workload = itemNum / threadNum;      // 每个线程要计算的 相乘的项数
    // (num / threadNum) 可能存在除不尽的情况，所以最后一个任务计算所有剩下的项数
    final int lastWorkload = itemNum - workload * (threadNum - 1);

    List<Callable<Matrix>> tasks = new ArrayList<>(threadNum);
    for (int i = 0; i < threadNum; i++) {
        if (i < threadNum - 1) {
            // 为了简洁，使用 Lambda 表达式替代要实现 Callable<Matrix> 的匿名内部类
            tasks.add(() -> matrix.pow(workload)); 
        } else {
            tasks.add(() -> matrix.pow(lastWorkload));
        }
    }

    ExecutorService threadPool = Executors.newFixedThreadPool(threadNum);
    List<Future<Matrix>> futures = threadPool.invokeAll(tasks); // 执行所有任务，invokeAll 会阻塞直到所有任务执行完毕

    Matrix result = primary.copy();
    for (Future<Matrix> future : futures) { // (matrix ^ n) * (f0, 0; f1, 0)
        result = result.mul(future.get());
    }

    threadPool.shutdown();

    return result.c;
}

复制代码

可以看到单线程情况下，使用矩阵运算的效率大概只有迭代计算的 1/3 左右 —— 既然如此，那我们耍流氓的把并行的线程数改为 10 线程吧：

BigInteger fi2 = parallelFibonacci(ITEM_NUM, 10); // 10 线程并行计算
复制代码

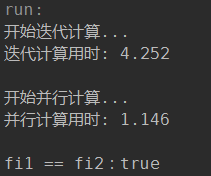
可以看到，此时并行计算的用时碾压了迭代计算 —— 迭代计算委屈的哭了，并行计算这流氓耍的相当漂亮。

好像有点不对劲，我这篇文章的标题似乎是 使用并行流 —— 并行流 呢？

其实前面都是铺垫 :) 在 parallelFibonacci 方法中，我们使用了线程池来并行的执行任务，我们来尝试将 parallelFibonacci 改为流式（即基于 Stream）风格的代码：

static BigInteger streamFibonacci(int itemNum, int threadNum) {
    final Matrix matrix = new Matrix(1, 1, 1, 0);
    final Matrix primary = new Matrix(1, 0, 1, 0);
    final int workload = itemNum / threadNum;
    final int lastWorkload = itemNum - workload * (threadNum - 1);
    
    // 流式 API
    return IntStream.range(0, threadNum)    // 产生 [0, threadNum) 区间，用于将任务切分
            .parallel()                     // 使流并行化
            .map(i -> i < threadNum - 1 ? workload : lastWorkload)
            .mapToObj(w -> matrix.pow(w))   // map    ->  mN = matrix ^ workload
            .reduce((m1, m2) -> m1.mul(m2)) // reduce ->  m = m1 * m2 * ... * mN
            .map(m -> m.mul(primary))       // map    ->  m = m * primary
            .get().c;                       // get    ->  m.c
}

复制代码

依旧在 10 线程的环境下运行下看看：

public static void main(String[] args) throws Exception {
    ...

    /* ------------------------------ */
    System.out.println("开始流式并行计算...");
    begin = System.nanoTime();

    BigInteger fi3 = streamFibonacci(ITEM_NUM, 10);

    end = System.nanoTime();
    time = (end - begin) / 1E9;
    System.out.printf("流式并行计算用时: %.3f/n/n", time);
    
    System.out.println("fi1 == fi2：" + (fi1.equals(fi2)));
    System.out.println("fi1 == fi3：" + (fi1.equals(fi3)));
}
复制代码

是的，使用并行流就是这么的简单，只要你会使用 Stream API —— 给它加上 .parallel() —— 它就并行化了。写了这么多年的 Java 代码，从 Java6 到 Java7 再到 Java8，这一刻，我真的感动了（容我擦擦眼泪）。

而且我们可以看到，在线程数相同的情况下，使用 streamFibonacci （并行流）时，用时要比 parallelFibonacci 方法更短。为了验证，我夸张一点，将线程数提高到 32：

BigInteger fi2 = parallelFibonacci(ITEM_NUM, 32);

...

BigInteger fi3 = streamFibonacci(ITEM_NUM, 32);
复制代码

可以看到，此时 parallelFibonacci 的运行时间反而比 10 线程的时候更长了，而 streamFibonacci 使用的时间却更短了 —— 流式 API 厉害了！

但这是什么原因呢？这个问题留给有兴趣的读者思考和探究吧。

值得注意的是，并行流的底层实现是基于 ForkJoinPool 的，并且使用的是一个共享的 ForkJoinPool —— ForkJoinPool.commonPool() 。为了充分利用处理器资源和提升程序性能，我们应该尽量使用并行流来执行 CPU 密集的任务，而不是 IO 密集的任务 —— 因为共享池中的线程数量是有限的，如果共享池中某些线程执行 IO 密集的任务，那么这些线程将长时间处于等待 IO 操作完成的状态，一旦共享池中的线程耗尽，那么程序中其他想继续使用并行流的地方就需要等待，直到有空闲的线程可用，这会在很大程度上影响到程序的性能。所以使用并行流之前，我们要注意到这个细节。

原文作者：mizhoux 原文地址： segmentfault.com/a/119000000…

推荐

大厂笔试内容集合（内有详细解析） 持续更新中....

ProcessOn是一个在线作图工具的聚合平台~

文末

欢迎关注个人微信公众号： Coder编程 欢迎关注 Coder编程 公众号，主要分享数据结构与算法、Java相关知识体系、框架知识及原理、Spring全家桶、微服务项目实战、DevOps实践之路、每日一篇互联网大厂面试或笔试题以及PMP项目管理知识等。更多精彩内容正在路上~ 新建了一个qq群：315211365，欢迎大家进群交流一起学习。谢谢了！也可以介绍给身边有需要的朋友。

文章收录至 Github: github.com/CoderMerlin… Gitee: gitee.com/573059382/c… 欢迎 关注 并star~