转载

求解稀疏优化问题——半光滑牛顿方法

加入极市专业CV交流群，与 6000+来自腾讯，华为，百度，北大，清华，中科院 等名企名校视觉开发者互动交流！更有机会与 李开复老师 等大牛群内互动！

同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流。关注 极市平台 公众号，回复 加群， 立刻申请入群~

来源：最优化理论和一阶方法知乎专栏

链接：https://zhuanlan.zhihu.com/p/92230537

本文已由作者授权转载，未经允许，不得二次转载

在这个一阶方法盛行的时代中，二阶方法看起来不那么受欢迎，能想到的优点好像只有“精度高”，但是原始的二阶方法（Newton,trust region,cubic regularizarion Newton）代价实在是太大了。为了权衡优缺点，出现了很多“似二非二”的算法，比如拟牛顿（quasi Newton），随机牛顿（stochastic Newton），次采样牛顿（subsample Newton）。这篇文章想讲下二阶方法一个很有意思的应用：利用半光滑牛顿（semismooth Newton）快速求解稀疏问题。目前已经出了许多相关文章，主要来自孙德锋老师的团队。有兴趣的可以参考他的主页。关于理论性的东西我就不说了（好像你会似的），这里我想简单阐述下这些文章的主要思想。

考虑一般问题：

求解稀疏优化问题——半光滑牛顿方法

其中求解稀疏优化问题——半光滑牛顿方法 ,并且 n 特别大；

f表示一个凸可微函数，例如
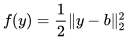
g表示一个闭真凸函数，一般为稀疏正则函数，比如 LASSO： , Fused LASSO，Clustered LASSO等

这个问题太general了，并且特别多的一阶方法可以去求解它，比如临近梯度方法（proximal gradient）以及它的加速版FISTA；交替方向乘子法（ADMM），原始对偶（primal dual）等等。这些方法说快也挺快的，毕竟只用到了一阶信息。但是他们没有考虑到两点：

A的存在，通常直接考虑
稀疏性的利用.

所以当n特别大的时候，这些方法也没那么快了。接下来我要讲的这个框架就完美的利用了这两点。大概思想是

利用ALM求解对偶问题，
利用二阶方法求解ALM的子问题，这里利用了问题本身的稀疏结构，使得该二阶方法既拥有了二阶方法的精度，又拥有一阶方法的复杂度，美哉！

一、增广拉格朗日方法求解（P）的对偶问题

首先，我们获得其对偶问题：

其中表示共轭函数，定义为：

求解稀疏优化问题——半光滑牛顿方法

接下来我们用增广拉格朗日方法（ALM）去求解这个对偶问题，首先获得增广拉格朗日函数：

在第k步迭代中，ALM迭代过程如下：

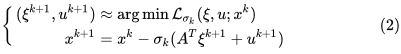
求解稀疏优化问题——半光滑牛顿方法

我们把（2）第一行单拿出来：

注意到,我们如果固定，对于u来说，上述问题是一个临近算子：

于是（3）就等价于

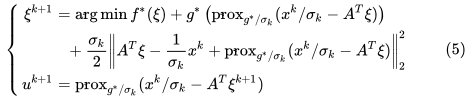
求解稀疏优化问题——半光滑牛顿方法

其实就是把闭式解（2）代入求解。好了，接下来的问题就是怎么求解这个 ,这玩意看起来好复杂啊，一点都不好解啊，甚至都不知道是不是光滑的。关键的地方来了，注意到中间包含了临近算子，我们将采样临近算子的一些性质去推导。虽然目标函数又臭又长，但是它是光滑的，并且它梯度的形式很简单！

二、半光滑牛顿法求解ALM子问题（5）

首先，我给出一些需要用到的，关于Moreau envelope的一些定义和性质。

定义

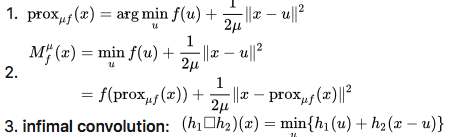
求解稀疏优化问题——半光滑牛顿方法

性质

1. 是光滑函数，并且它的梯度为: 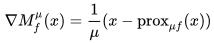求解稀疏优化问题——半光滑牛顿方法

2.Moreau分解：

Proof.1. 严格的证明要写好几页，我就不写了，这里大概讲下，感兴趣的参考文献【2】的定理6.60 。

我们首先把表达成infimal convolution（定义3）的形式。令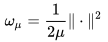求解稀疏优化问题——半光滑牛顿方法 ,于是我们得到了：

而对于infimal convolution，我们知道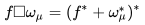求解稀疏优化问题——半光滑牛顿方法（这个等式满足需要一些条件，f 和为proper convex function）。

接着我们说明是u -strongly convex的，因为对于一个extended real function，它的共轭函数一定是closed and convex. 所以是convex，而是 -smooth，根据conjugate correspondence 定理，我们知道它的共轭是u-strongly convex。综合就得到了是 u-strongly convex的。

最后，因为和互为共轭，再次根据conjugate correspondence 定理，得到是-smooth的，也就等价于是-smooth的。

而对于它的梯度的形式，也是从infimal convolution入手，令表示infimal convolution的解，我们有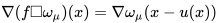求解稀疏优化问题——半光滑牛顿方法 ,利用的形式，我们就得到了最终的式子。

Proof.2. 还是见文献【2】的定理6.45 .（因为证明要用到了好多定理，就不证明了）

我们接下来去简化关于的求解

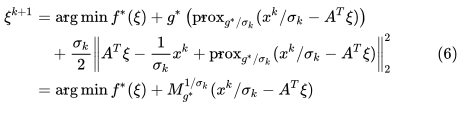
求解稀疏优化问题——半光滑牛顿方法

其中第二个等式利用了定义2。接下来我们利用半光滑牛顿法去求解问题（6）。

首先给出其梯度以及Hessian矩阵。令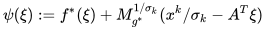求解稀疏优化问题——半光滑牛顿方法，根据性质1，我们知道这个函数是光滑的，并且它的梯度为：

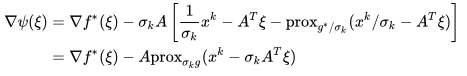
求解稀疏优化问题——半光滑牛顿方法

第一个等式是性质1，第二个等式是性质2.

半光滑牛顿法是要求解如下方程

求解稀疏优化问题——半光滑牛顿方法

定义它的广义Hessian矩阵为：

半光滑牛顿法的基本迭代为

其中求解稀疏优化问题——半光滑牛顿方法。

为什么是半光滑牛顿？因为这个Hessian矩阵不唯一，为什么不唯一，因为临近算子的jacb矩阵不唯一，或者说临近算子不光滑。从这个式子来看，也没什么不一样啊，为什么要用二阶方法呢？接下来轮到稀疏性发挥作用了。由于我们的g是稀疏函数。所以关于其临近算子的jacbi矩阵通常是也是稀疏矩阵。这里我们以为例。当求解稀疏优化问题——半光滑牛顿方法 , 它的proximal operator为：

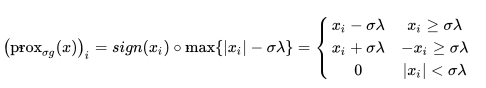
因为这个算子是可分得（各个分量互不影响），所以求解稀疏优化问题——半光滑牛顿方法一定是对角矩阵。关注第i个分量：

求解稀疏优化问题——半光滑牛顿方法

画图的话大概长这样，中间那条横线的两端分别为- 和。左右两条线斜率都为1.

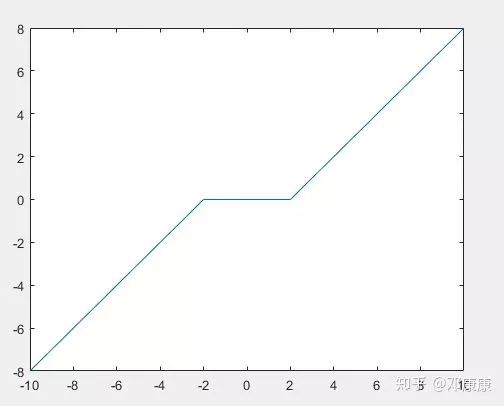
所以很容易得到最终其对角元为

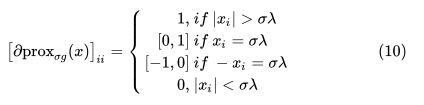
求解稀疏优化问题——半光滑牛顿方法

所以对于（8）的第二部分，我只需要将对角元非零的相对应的A的子矩阵相乘即可，这大大的降低了计算量。

看下图：

左边括号里面的就是，当
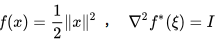
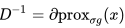是一个对角矩阵。图中就是（9）中的
蓝色的就是我们实际计算的部分，红色部分为对角元为0对应的A的列，白色部分为（10）式子中的第二三种情况，你自己选择要零还是非零（通常直接选择0，并且实际中这种情况极其少见，毕竟刚好相等有点难）。

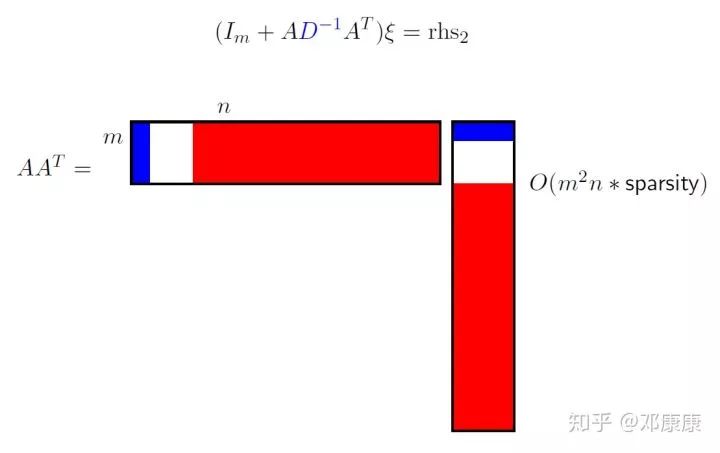
这样子的做法，既保证了快速收敛（比较少的迭代），又保证了每步的复杂度差不多为一阶算法（取决于稀疏程度）。妙啊~~~~

三、总结

首先我讲的这个是一个general的算法框架，非光滑函数不限于Lasso，可以是其他稀疏正则。差别就在于如何计算其临近算子的jacbi矩阵。目前主要的一些正则函数都出了文章了，参考孙老师主页http://www.polyu.edu.hk/ama/profile/dfsun/
虽然非光滑函数可以是任意凸的函数，但如果没有稀疏性或者其他结构的话，这个方法不见得有效。所以说没有一个一统江湖的方法，只有合适某类问题的方法。

参考文献：

[1] Li X, Sun D, Toh K C. A highly efficient semismooth Newton augmented Lagrangian method for solving Lasso problems[J]. SIAM Journal on Optimization, 2018, 28(1): 433-458.

[2]Beck, Amir. First-Order Methods in Optimization || Front Matter[J]. 10.1137/1.9781611974997:i-xii.

-End-

*延伸阅读

优化 | 怎么判断一个优化问题是凸优化还是非凸优化？
谷歌最新人工智能研究：仅利用稀疏轮廓位置「重构」图像
活动 | 加入极市原创作者行列，实现一个小目标

CV细分方向交流群

添加极市小助手微信 （ID : cv-mart） ，备注： 研究方向-姓名-学校/公司-城市 （如：目标检测-小极-北大-深圳），即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割、OCR、姿态估计等极市技术交流群（已经添加小助手的好友直接私信），更有每月大咖直播分享、真实项目需求对接、干货资讯汇总，行业技术交流，一起来让思想之光照的更远吧~

求解稀疏优化问题——半光滑牛顿方法