转载

二叉树遍历Java(递归+迭代)：前序、中序和后续遍历（双栈法+Deque法）

LeetCode 传送门（中序遍历动画是错的）： LeetCode 二叉树专题讲解

参考链接：

树、二叉树的前中后层序遍历（递归、非递归Java实现）

树的遍历

二叉树的前序，中序，后序遍历方法总结

先根遍历、中根遍历和后根遍历

核心思维模型：对于二叉树的遍历，首先要将 Base Case 具体化出来，最底层的子节点不是没有左、右两个子节点，应该将其左、右两个子节点用 null 表示出来。即最底层子节点的左、右子节点都是 null。

在每次递归遍历中，该子节点相对于本次遍历都是一个根节点，它的左右子节点即使都是null，也是有左右子节点的！对于递归方法，最底层子节点和一个普通的根节点没有任何区别。

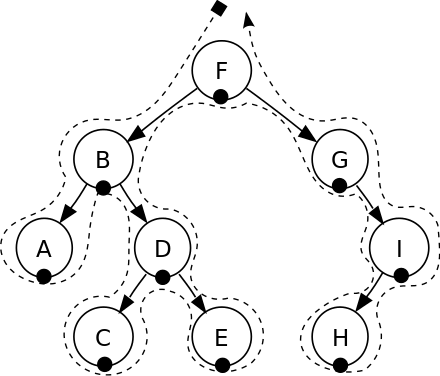
先根遍历递归 Pre-Order Traversal

深度优先遍历 - 前序遍历： F, B, A, D, C, E, G, I, H.

public void preOrder(BinaryTreeNode root) {
    //Base Case
    if(root == null) return;
    System.out.print(root.value);
    
    //遍历左子树
    preOrder(root.left);
    
    //遍历右子树
    preOrder(root.right);
}
复制代码

先根遍历迭代

深入优先遍历二叉树需要借助栈结构来实现。

/**
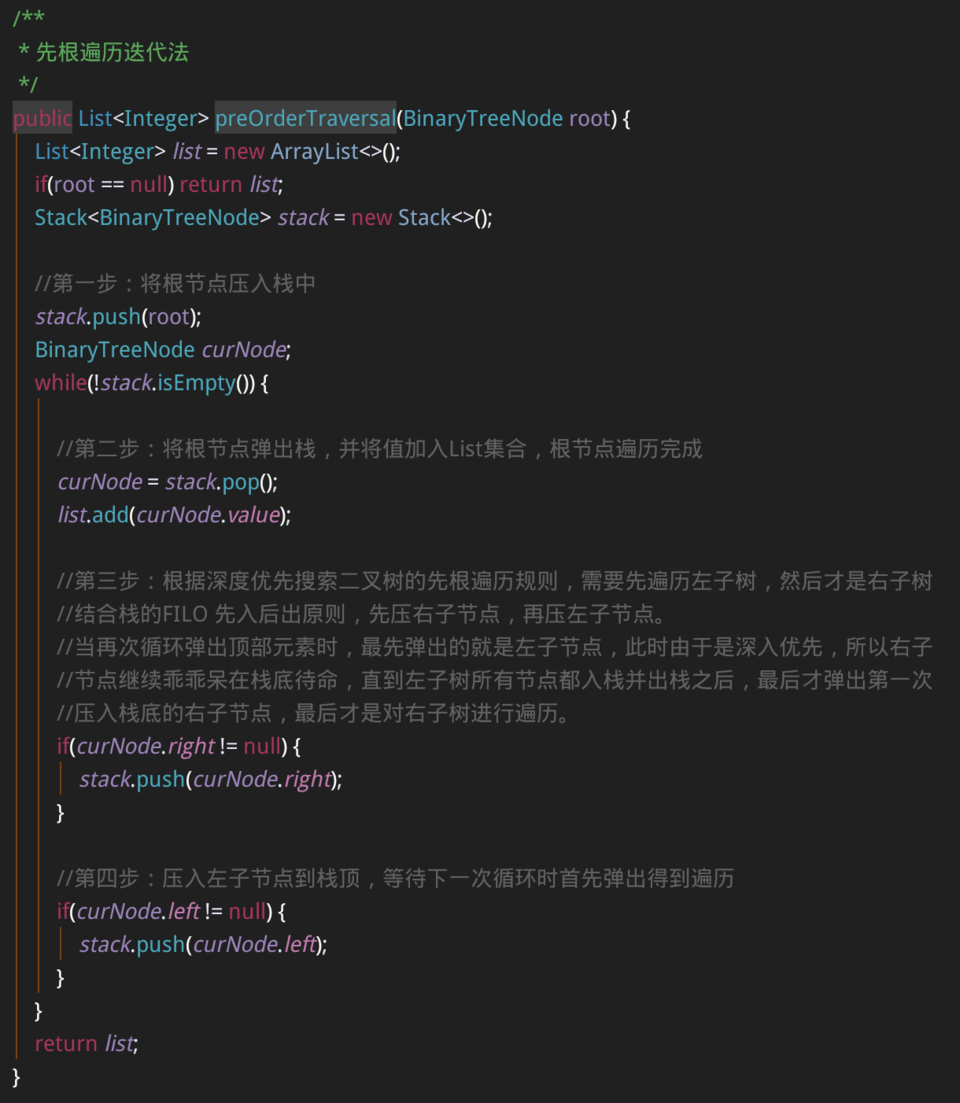
 * 先根遍历迭代法
 */
public List<Integer> preOrderTraversal(BinaryTreeNode root) {
    List<Integer> list = new ArrayList<>();
    if(root == null) return list;
    Stack<BinaryTreeNode> stack = new Stack<>();

    //第一步：将根节点压入栈中
    stack.push(root);
    BinaryTreeNode curNode;
    while(!stack.isEmpty()) {

        //第二步：将根节点弹出栈，并将值加入List集合，根节点遍历完成
        curNode = stack.pop();
        list.add(curNode.value);

        //第三步：根据深度优先搜索二叉树的先根遍历规则，需要先遍历左子树，然后才是右子树
        //结合栈的FILO 先入后出原则，先压右子节点，再压左子节点。
        //当再次循环弹出顶部元素时，最先弹出的就是左子节点，此时由于是深入优先，所以右子
        //节点继续乖乖呆在栈底待命，直到左子树所有节点都入栈并出栈之后，最后才弹出第一次
        //压入栈底的右子节点，最后才是对右子树进行遍历。
        if(curNode.right != null) {
            stack.push(curNode.right);
        }

        //第四步：压入左子节点到栈顶，等待下一次循环时首先弹出得到遍历
        if(curNode.left != null) {
            stack.push(curNode.left);
        }
    }
    return list;
}
复制代码

中根遍历递归 In-Order Traversal

深度优先遍历 - 中根遍历： A, B, C, D, E, F, G, H, I.

public void inOrder(BinaryTreeNode root) {
    if(root == null) return;
    inOder(root.left);
    System.out.print(root.value);
    inOder(root.right);
}

复制代码

中根遍历迭代法

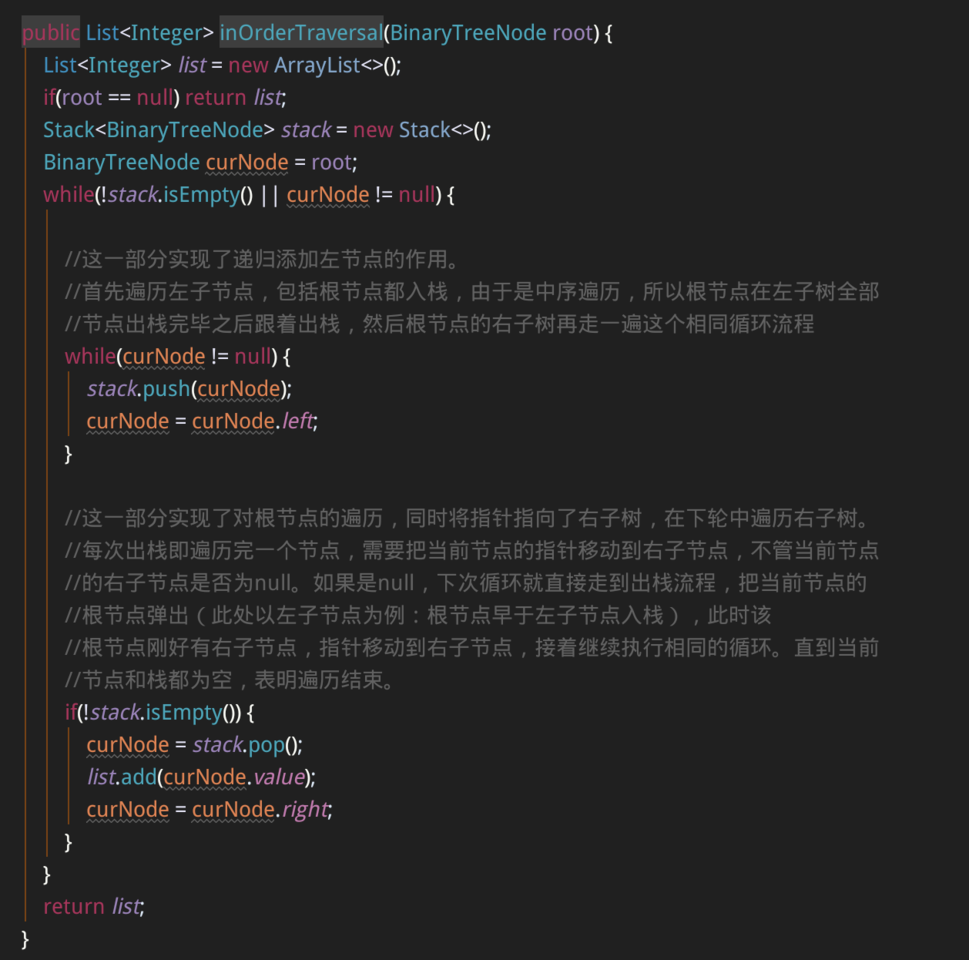
public List<Integer> inOrderTraversal(BinaryTreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null) return list;
        Stack<BinaryTreeNode> stack = new Stack<>();
        BinaryTreeNode curNode = root;
        while(!stack.isEmpty() || curNode != null) {

            //这一部分实现了递归添加左节点的作用。
            //首先遍历左子节点，包括根节点都入栈，由于是中序遍历，所以根节点在左子树全部
            //节点出栈完毕之后跟着出栈，然后根节点的右子树再走一遍这个相同循环流程
            while(curNode != null) {
                stack.push(curNode);
                curNode = curNode.left;
            }

            //这一部分实现了对根节点的遍历，同时将指针指向了右子树，在下轮中遍历右子树。
            //每次出栈即遍历完一个节点，需要把当前节点的指针移动到右子节点，不管当前节点
            //的右子节点是否为null。如果是null，下次循环就直接走到出栈流程，把当前节点的
            //根节点弹出（此处以左子节点为例：根节点早于左子节点入栈），此时该
            //根节点刚好有右子节点，指针移动到右子节点，接着继续执行相同的循环。直到当前
            //节点和栈都为空，表明遍历结束。
            if(!stack.isEmpty()) {
                curNode = stack.pop();
                list.add(curNode.value);
                curNode = curNode.right;
            }
        }
        return list;
    }

复制代码

后根遍历递归 Post-Order Traversal

深度优先搜索 - 后序遍历： A, C, E, D, B, H, I, G, F.

public void postOrder(BinaryTreeNode root) {
    if(root == null) return;
    postOrder(root.left);
    postOrder(root.right);
    System.out.print(root.value);
}
复制代码

后根遍历迭代法（双栈法）

/**
     * 参考：https://segmentfault.com/a/1190000016674584?utm_medium=referral&utm_source=tuicool
     * 仔细观察一下后序遍历的顺序：左 -- 右 -- 根
     * 根节点在最后，对照先序遍历的顺序：根 -- 左 -- 右
     * 这里我们可以想到，将先序遍历微调为：根 -- 右 -- 左的顺序，这个微调很简单，只是在push节点到栈
     * 里时，先push左节点，再push右节点，此时栈顶是右节点，那么下次循环就会先弹出右节点，此时，
     * 再把弹出的右节点push到反向栈 stackReverse 里即可。
     * 核心：我们只需要增加一个栈来反向输出微调之后的先序遍历的每个节点，就可以得到后序遍历顺序。
     */
    public List<Integer> postOrderTraversal(BinaryTreeNode root) {
        List<Integer> list = new ArrayList<>();
        if (root == null) return list;
        Stack<BinaryTreeNode> stack = new Stack<>();
        Stack<BinaryTreeNode> stackReverse = new Stack<>();
        stack.push(root);
        BinaryTreeNode curNode;
        while (!stack.isEmpty()) {
            curNode = stack.pop();
            stackReverse.push(curNode);
            if (curNode.left != null) {
                stack.push(curNode.left);
            }
            if(curNode.right != null) {
                stack.push(curNode.right);
            }
        }

        while(!stackReverse.isEmpty()) {
            curNode = stackReverse.pop();
            list.add(curNode.value);
        }
        return list;
     }
复制代码

注意：由于双栈法使用了额外的栈空间，也增加了一个循环，还可以优化。

后根遍历迭代法（使用Deque，即双向队列法）

/**
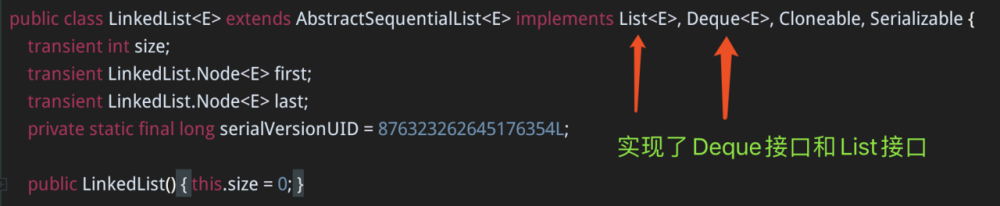
 * 双向队列法和先序遍历迭代的区别只是使用了 Deque 这种链表数据结构，每次都
 * 从链表头插入新节点。由于 LinkedList 本身已经实现了 Deque 接口和List接口，因此
 * LinkedList 可以作为一个双向队列来使用，同时本身也是List的实现类。可以很方便地
 * 实现将新节点插入到表头的需求。
 */
 public List<Integer> postOrderTraversalByDeque(BinaryTreeNode root) {
     LinkedList<Integer> resultList = new LinkedList<>();
     if (root == null) return resultList;
     Stack<BinaryTreeNode> stack = new Stack<>();
     stack.push(root);
     BinaryTreeNode curNode;
     while(!stack.isEmpty()) {
         curNode = stack.pop();
         resultList.addFirst(curNode.value);
         if (curNode.left != null) {
             stack.push(curNode.left);
         }
         if (curNode.right != null) {
             stack.push(curNode.right);
         }
     }
     return resultList;
 }

复制代码

原文 https://juejin.im/post/5dd8b29551882572ef06c5af

正文到此结束