Double为什么会失真？
一个小数的组成：在我国，小数表示由三部分组成，分别是整数+小数点（分隔符）+小数。
2、小数为什么会被称为浮点数
浮点数是属于有理数中某特定子集的数的数字表示，在计算机中用以近似表示任意某个实数。具体的说，这个实数由一个整数或定点数（即尾数）乘以某个基数（计算机中通常是2）的整数次幂得到，这种表示方法类似于基数为10的科学计数法。
对于浮点数可以这样简单的理解：浮点数就是小数点可以任意浮动的数字。
在计算机的机器语言中，只有二进制，机器语言只能识别0和1。所以，计算机也是不可能存储小数的，所以需要有另一种变通的存储方案。这种方案就是指数方案：
通过观察以上的图片不难发现，作为一个小数3.14。如果使用指数表现形式的话（3.14E0），其写法是多种多样的，这样写的话，小数点就可以任意浮动了。
3、Java中浮点数的表示方法
对于float来说，4个字节，32位，0-22位表示尾数，23-30(8位)表示指数，31位表示符号位。
对于double来说，8个字节，64位，0-51表示尾数，52-62(11位)表示指数，63位最高位表示符号位。
二、浮点数在内存中是如何存储的？
我们知道，任何数据在计算机内存中都是用‘0/1’来存储的，浮点数亦是如此。因此十进制浮点数在存储时必定会转换为二进制的浮点数。
在内存中使用二进制的科学计数法来存储，因此分为阶码（即指数）和底数，由于也有正负之分，所以还有一位符号位。
以float为例，float在内存中的存储为：
float 符号位(1bit) 指数(8 bit) 尾数(23 bit)
double 符号位(1bit) 指数(11 bit) 尾数(52 bit)
float在内存中占8位，由于阶码实际存储的是指数的移码，假设指数的真值是e,阶码为E，则有E=e+(2^n-1 -1)。其中 2^n-1 -1是IEEE754标准规定的指数偏移量，根据这个公式我们可以得到 2^8 -1=127。于是，float的指数范围为-128 +127，而double的指数范围为-1024 +1023。其中负指数决定了浮点数所能表达的绝对值最小的非零数；而正指数决定了浮点数所能表达的绝对值最大的数，也即决定了浮点数的取值范围。
float的范围为-2^128 ~ +2^127，也即-3.40E+38 ~ +3.40E+38；
double的范围为-2^1024 ~ +2^1023，也即-1.79E+308 ~ +1.79E+308
这里使用移位存储，对于float来说，指数位加上127，double位加上1023(这里指的是存储，在比较的时候要分别减去127和1023)
移位存储本质上是为了保证+0和-0的一致性。
以float指数部分的这8位来分析，
那么这8位组成的新的字节，我们来用下面的一串数字表示：0000 0000
首先，我们假设不使用移位存储技术，而是单单看看这个 8位组成的新字节，到底能表示多少个数： 0000 0000 -1111 1111 即0-255，一共256个数。
但是我们知道这8位数既要表示正数也要表示负数。
所以将左边第一位拿出来表示正负的符号：
第一个区间：
0 000 0000 - 0 111 1111
即+0 到127
第二个区间：
1 000 0000 - 1 111 1111
即 -0到-127
这就是问题的所在:怎么会有两个0，一个正零，一个负零。
这时候使用移位存储：float使用127(0111 1111)
表示0：0+127=127 即 0000 0000 +0111 1111=0111 1111
表示1：1+127=128 即 0000 0001 +0111 1111=1000 0000
表示128：128+127=255 即 1000 0000+0111 1111=1111 1111
最大的正数，再大就要溢出了。
表示-1： -1+127=126=127-1 即 0111 1111-0000 0001=0111 1110
表示-1： -2+127=125=127-2 即 0111 1111-0000 0010=0111 1101
表示-127： -127+127=0 即0111 1111-0111 1111=0000 0000
最小的负数，在校就溢出了。
三、浮点数的进制转换
1、十进制转二进制
主要看看十进制转二进制，整数部分和小数部分分开处理
-
整数部分：整数除以2，得到一个商和余数，得到的商继续除以2并得到一个商和一个余数，继续除以2操作直至商为0，上述操作得到一系列余数，从最后一个余数开始直至第一个余数，这一系列0/1即为转换后的二进制数。
-
小数部分：乘以2，然后取出整数部分，将剩下的小数部分继续乘以2，然后再取整数部分，一直取到小数部分为零为止。如果永远不为零，则按要求保留足够位数的小数，最后一位做0舍1入。将取出的整数顺序排列。
从以上转换过程可以看出，并不是任何一个十进制小数都可以用二进制精确表示出来。一个在0到1之间的小数P可用如下形式表示：
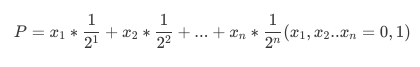
从这个式子中我们也可看出二进制表示出的小数是分段的，这也是为什么在Java中浮点数很多时候并不是十分精确的表示十进制小数的根本原因。
public static void main(String[] args) {
float f1=20f;
float f2=20.3f;
float f3=20.5f;
double d1=20;
double d2=20.3;
double d3=20.5;
System.out.println(f1==d1);
System.out.println(f2==d2);
System.out.println(f3==d3);
}
true false true
以20.3举例：
20转换后变为 10100
0.3 要转换二进制，需要乘2, 乘完之后 取整数部分，然后用乘的结果减去整数部分， 然后 接着乘2, 直至最后没有小数或者小数出现循环, 即乘完.
0.3 * 2 = 0.6 (0) 0.6 * 2 = 1.2 (1) 0.2 * 2 = 0.4 (0) 0.4 * 2 = 0.8 (0) 0.8 * 2 = 1.6 (1)
计算到这里， 将再出现0.6,进入循环了，所以，结果
0.3 = 0.010011001…1001
所以20.3 = 10100.010011001…1001 (二进制).
2、二进制的科学记数法表示
20.3 = 10100.010011001…1001 (二进制)=1.01000100110011E10…..（十进制科学计数）=1.01000100110011E100…..(二进制科学计数)
这里使用移位存储，对于float来说，指数位加上127，double位加上1023(这里指的是存储，在比较的时候要分别减去127和1023)
同时要注意一点，以float为例，最高位表示的是整个数的符号位，指数位一共8位，最高位表示的是指数位的正负，因为有可能是E-100这样的情况，所以虽然有8位，最高位只是符号位，剩下7位才是表示真正的数值，这也是使用移位存储的原因。
对于一个数字，只要不超过和float的范围，同时小数部分不是无限小数，就可以和对应的double类型相等。
3、浮点数舍入规则
以52位尾数的双精度浮点数为例，舍入时需要重点参考第53位。
若第53位为1，而其后的位数都是0，此时就要使第52位为0；若第52位为0则不用再进行其他操作，若第52位为1，则第53位就要向52位进一位。
若第53位为1，但其后的位数不全为0，则第53为就要向第52位进一位。
若不是以上两种情况，也即53位为0，那么就直接舍弃不进位，称为下舍入。
浮点数舍入规则也就证明了为何在上文中提到的浮点数舍入中，相对舍入误差不能大于机器ε的一半。
对于java来说，一般float类型小数点后保留7位，而double类型小数点后保留15位。
这个原因也是因为尾数的数据宽度限制
对于float型来说，因为2^23 = 8388608
同时最左一位默认省略了，故实际能表示2^24 = 16777216个数，最多能表示8位，但绝对精确的只能表示7位。
而对于double型来说，2^52 = 4503599627370496，共16位。加上省略的一位，能表示2^53 = 9007199254740992。故double型最多能表示16位，而绝对精确的只能表示15位。
4、机器ε
机器ε表示1与大于1的最小浮点数之差。不同精度定义的机器ε不同。以双精度为例，
双精度表示1是
1.000……0000（52个0） × 2^0
而比1大的最小的双精度是（其实还能表示更小的范围，后文中会提到，但并不影响这里的机器ε）
1.000……0001 × 2^0
也即
2^-52 ≈ 2.220446049250313e-16。所以它就是双精度浮点数的机器ε。
在舍入中，相对舍入误差不能大于机器ε的一半。
对于双精度浮点数来说，这个值为0.00000005960464477539。
所以在Java中double类型中连续8个0.1相乘，就会出现表示不精确的情况。
参考：
https://baijiahao.baidu.com/s?id=1618173300159774003&wfr=spider&for=pc
https://www.cnblogs.com/Vicebery/p/9997636.html
https://blog.csdn.net/Return_head/article/details/88623060
https://blog.csdn.net/u011277123/article/details/95774544
https://blog.csdn.net/endlessseaofcrow/article/details/81269079正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
