为了更好的读源码，你必须搞定这些java基础知识！（位运算，进制转换和原码，反码和补码）

不知道上一篇文章看的怎么样了： 害怕面试被问HashMap？这一篇就搞定了！

在这篇文章中，我比较详细的分析了为什么HashMap的初始化容量是16以及为什么容量的大小要是2的整数次幂！

不知道你看懂了没，如果你看的懵懵懂懂的话，我猜你对以下基础知识一定不那么熟悉：

1. java中的位运算
2. 进制之间的转换
3. 原码，反码和补码

怎么样，对这些基础知识掌握的如何，这些可以说都是大学时候学的计算机基础了，不过，我知道你当时肯定没学会，即使学会了也忘得差不多了。

其实吧，这些基础知识真的超级重要，你看，现在阅读源码的时候因为这些基础知识不过关而遇到坎了吧。

别担心，今天咱们一起越过这道坎！

先从进制转换开始

对于进制转换这个啊，说来惭愧，我之前学过不止一次，曾经有一次还花了很长时间，做笔记，画图，弄了满满的一张A4纸，当时觉得对进制转换这块完全OK了，以后再也不怕进制转换了。

可是嘞后来读源码的时候遇到进制转换的时候还是觉得不知所措，发现之前学的都忘得差不多了，唉。

所以啊，对于学习，我们可不能一味的向前学习新知识，对于之前的知识也要经常回顾，温故而知新，可以为师矣嘛

好啦，咱们这次再来一起学习下进制转换吧！

对于进制转换啊，其实我们的重点主要放在与十进制之间的各种转换即可，因为这才是我们平常使用频率比较高的，所以要优先熟练的掌握这些。

啥是二进制

十进制我们再熟悉不过了，那啥是二进制嘞，简单来说，二进制就是用0和1来表示的数值，在十进制中逢十进一，借一当十，而二进制呢？那就是逢二进一，借一当二，这个好懂，但是这里我要说些概念。

什么嘞？后面我们要说到原码，反码和补码，这里先说下，它们都是二进制数，也就是都是由0和1表示的，单是可能具体的数值不一样。

我们要知道，对于计算机而言，它只认识0和1，所以对于数据在计算机中的存储都是以二进制的形式来存储的，好了，先有这个概念。

十进制与二进制之间的一个规律

先来看一个图：

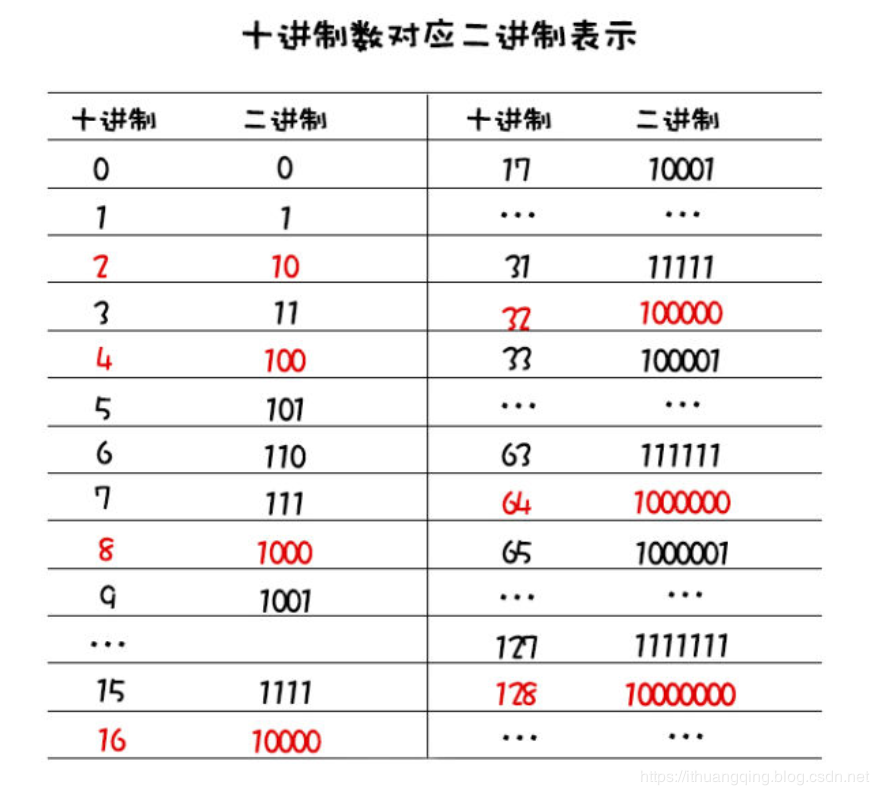
不知道你看出来什么没，主要看标红的，前面说过了，二进制就是逢二进一，那么上图中标红的二进制是不是都是产生进位的数值，啥意思嘞，比如二进制11，并没有产生进位，如果要产生进位，那就要再加一，然后就会产生进位得100，你看是不是？

再看进位产生的二进制对应的十进制是不是这些数值：

2，4，8，16……

那么你看这些产生进位的二进制数值有什么特点，是不是最高位（最左边）是不是都是1，其他都是0，所以这里就有个规律：

十进制下的2的整数次幂的数的二进制的高位都是1，其他全是0，然后看是2的几次幂，是几就有几个零

好吧，我相信这里没什么难理解的！

ps：看到这里你是不是更容易理解为什么HashMap的容量要是2的整数次幂了呢？

二进制转十进制

那么二进制的数据怎么转换成十进制呢？我们看十进制的11从右往左是不是依次代表1个1,1个10，加起来也就是11.

那么来看二进制1011怎么表示，看下面的：

二进制的数从右向左各个位表示十进制的含义：

第一个1表示：1的个数（有1个1）

第二个1表示：2的个数（有1个2）

第三个0表示：4的个数（有0个4）

第四个1表示：8的个数（有1个8）

为什么是1（默认右边第一位开始），2，4，8呢？注意上面说的那个规律，所以上面的加起来就是1+2+0+8等于11。

怎么样？二进制转十进制是不是比较简单，其实后面还有个公式，等下再说，我们继续往下看

十进制转二进制

知道吗？这里有个通用的方法那就是： 除以2，余数逆序排列 ，看个例子吧：

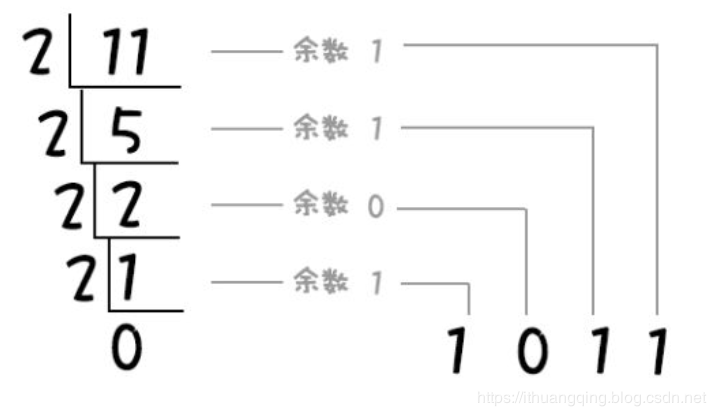
也就是说十进制转换成二进制的话，那就用十进制的数除以2，然后取余数之后将余数逆序排列就是对应的二进制数了，怎么样是不是更简单，我们接着往下看

十进制与其他进制之间的转换

我们之前就说过，对于进制转换我们重点关注的就是与十进制之间的转换，我们上面介绍了二进制和十进制之间的互相转换，那么还有八进制和十六进制，它们与十进制之间的转换又是怎样呢？

这里首先记住十进制转换其他进制的通用方法：

“除基数B取余，逆序排列”方法可以将十进制数转换为任意进制数。

那么这个基数B是啥呢？比如十进制转换成二进制，那么这个基数B就是2，知道了吧！

那么其他进制转换成十进制怎么整嘞？记住这个公式：

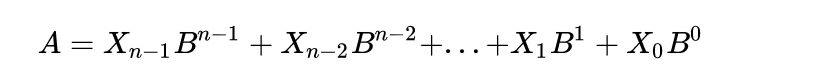
这个公式可以概括为：“按权展开”—其他进制转换为十进制（B表示各进制的基数，n表示位数）

举个例子，比如之前1011这个二进制转换成十进制就可以这样：

就是这样的啦，至于其他的什么八进制和十六进制之间的互相转换什么的，不怎么常用，感兴趣的自行了解，对了，我平常都是直接搜索在线进制转换的:joy:

进攻位运算

了解了进制转换，尤其是十进制和二进制之间的转换之后我们就可以开始学习java中的位运算了，因为位运算实际上都是对二进制进行操作的，接下来我将逐步分析java中常见的位运算。

左移 <<

举个栗子，5 << 2 将5左移2 结果为20 为啥？注意是对二进制进行的操作，来看：

首先会将5转为二进制表示形式(java中，整数默认就是int类型,也就是32位):

怎么去理解，首先在Java中，整数默认就是int类型，也就是占4个字节32位，你就可以想成这样

0000 0000 0000 0000 0000 0000 0000 0000

这就是32位，但是每位上都是0，这是一个标准，用于后面的比较，比如5的二进制是

0000 0000 0000 0000 0000 0000 0000 0101

然后把它与标准的进行对比，也就是这样：

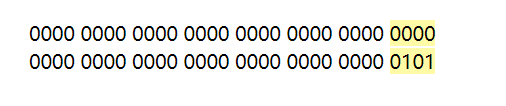
这时候的区别就在后四位，然后将5左移（<<）2，也就是5的二进制以标准为参考整体左移2位，也就是这样：

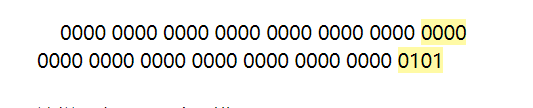
这样一来，就产生了错位，看图：

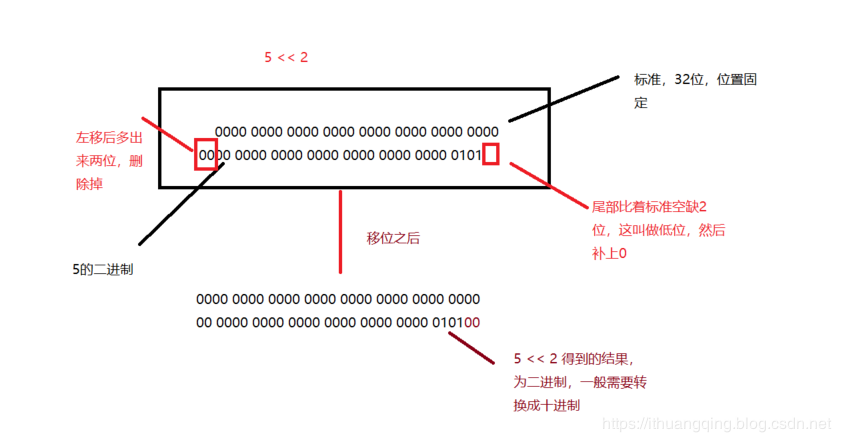
不过这时候看着总是有点别扭，应该都是四位四位的在一块吧，所以从低位开始，四位一组，就成了这样

0000 0000 0000 0000 0000 0000 0001 0100

换算成十进制就是20了 这就是5 << 2得到结果的由来。

右移 >>

还是先将5转为2进制表示形式：

0000 0000 0000 0000 0000 0000 0000 0101 然后右移2位，高位补0：

0000 0000 0000 0000 0000 0000 0000 0001

看图：

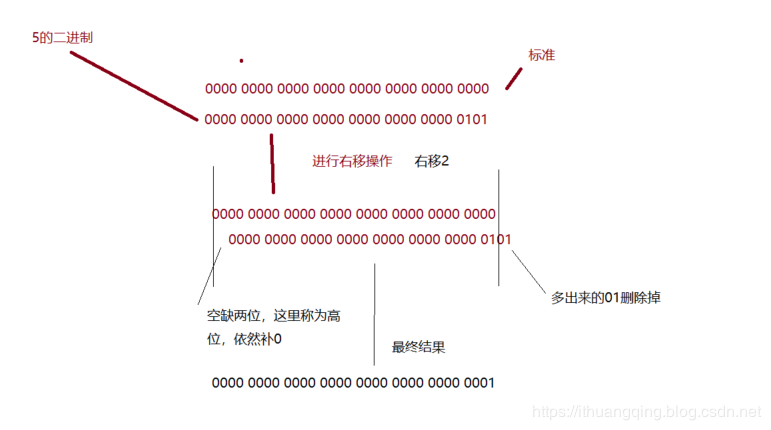
仔细看图分析分析:smiley:

无符号右移 >>>

先记住这句话： 正数右移，高位补0，负数右移，高位补1，负数无符号右移，高位补0 正数无符号右移 ，高位补0 正数换算成二进制后的最高位为0，负数的二进制最高位为1

接下来依然是看例子，在此之前我看过好多别人写的，发现好多都喜欢用5举例子你知道为啥吗:joy:

5换算成二进制是： 0000 0000 0000 0000 0000 0000 0000 0101

5右移3位后结果为0，0的二进制为： 0000 0000 0000 0000 0000 0000 0000 0000 // (这里高位补0)

-5换算成二进制是： 1111 1111 1111 1111 1111 1111 1111 1011

-5右移3位后结果为-1，-1的二进制为： 1111 1111 1111 1111 1111 1111 1111 1111 // (高位补1)

-5无符号右移3位后的结果 536870911 换算成二进制： 0001 1111 1111 1111 1111 1111 1111 1111 // (高位补0)

这里需要注意了： 以上说的都是右移的情况，如果是左移，无论是正数还是负数，低位都是用0补

时间关系，就不赘述了。

位与 &

其实核心都是二进制，所以掌握好进制转换是关键，看看位与 &是怎么计算的：

这里要看两个操作数的二进制的各个位的对应情况，总结起来也就是：

有0则0，否则为1

什么意思呢？我们举一个例子来看看

我们猜这个结果是什么，答案是

注意这里可不是6除以3，它是这样计算的，首先6和3都要转成二进制，6的二进制是110，3的二进制是11也就是011，那么这样运算

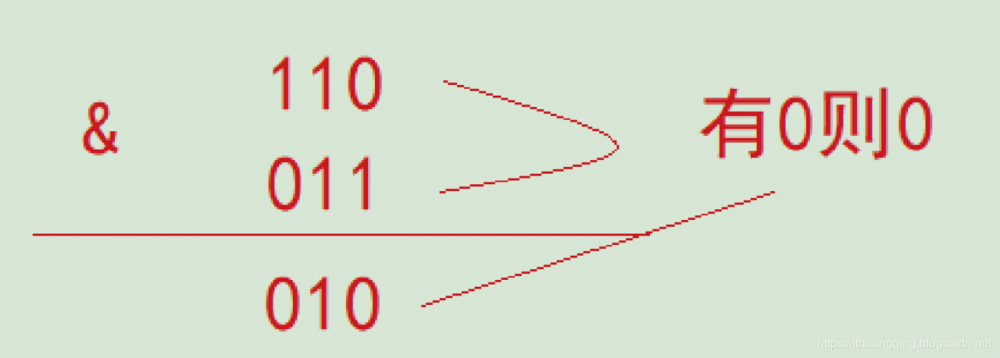
我相信看图就能明白的，而二进制的010就是2啦，这就是位与的操作，对于或和亦或其实同样道理，我们继续来看：

位或 |

规则就是：有1则1

看例子：

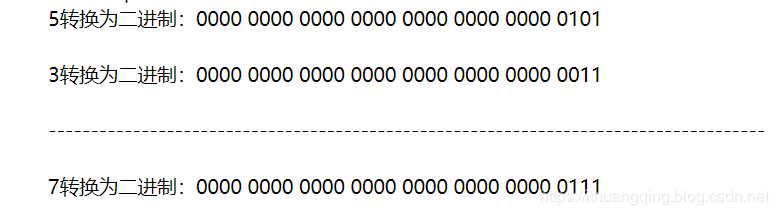
位异或 ^

规则是：相同则0，不同则1

看例子：

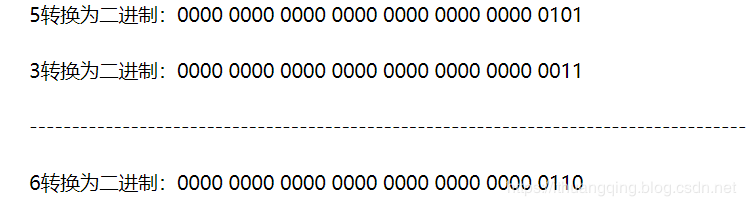
有点难懂的位非 ~

这是网站随便找的一个例子，你看看，求~5，得-6，为啥？

它这里的规则是：操作数的第n位为1，那么结果的第n位为0，反之。

不知道你懂吗？有这么一个解释：

6的二进制数为： 0000 0000 0000 0000 0000 0000 0000 0110 然后6的二进制反码为： 1111 1111 1111 1111 1111 1111 1111 1001 将反码+1得到-6的补码二进制数：1111 1111 1111 1111 1111 1111 1111 1010

所以这里就牵涉到原码，反码和补码了，另外还有个重点的点就是：

负数在计算机中是以补码的形式存在的

好了，我们赶紧来看看什么是原码，反码和补码吧！

最后攻克原码，反码和补码

这是非常重要的概念，需要熟练掌握，要记得。开始之前，先上一个重要的结论：

数据在计算机中的存储是二进制的形式，二进制简单来说就是0和1组合的，无论原码，反码还是补码，都是二进制的形式

其次我们要注意的点就是正数和负数的原码，反码和补码，是有区别的。

原码

什么是原码嘞？

对于正数来说，我们把它的绝对值转换成的二进制数叫做正数的原码，对于负数来说我们把它的绝对值转换成的二进制数，然后最高位补1，称为原码。看看，还是有区别的。

比如 ：

00000000 00000000 00000000 00000101 是 5的 原码。

10000000 00000000 00000000 00000101 是 -5的 原码。

这里有个点就是最高位是0代表正数，是1代表负数。

正数和负数在计算机中怎么表示的

接下来就是在计算机中的表示：

对于正数：原码，反码和补码都是一样的，所以在计算机中怎么说都一样，反正就是本身转换成二进制的结果，可以说原码，也可以说补码，因为都是一样的

对于负数：原码，反码和补码是不一样的，在计算机中 负数是以补码的形式存在的

所以说，重点聚焦在负数上，看它的反码和补码是怎么表示的

反码

那反码是啥嘞？

负数的反码为对该数的原码除符号位外各位取反[每一位取反(除符号位)]。

这里有个符号位，啥？还记得刚刚说的吗？

最高位是0代表正数，是1代表负数。

也就是最左边的那一位。

取反操作指： 原为1，得0；原为0，得1。（1变0; 0变1）

比如：

正数00000000 00000000 00000000 00000101 的反码还是

00000000 00000000 00000000 00000101

负数10000000 00000000 00000000 00000101 的反码则是

11111111 11111111 11111111 11111010

另外啊反码是相互的，因此也可称：

10000000 00000000 00000000 00000101 和 11111111 11111111 11111111 11111010互为反码。

不过这里有个问题，那就是+0和-0，什么意思呢？

原码和反码在表示数的时候的有点尴尬啊，比如表示零的时候，同样都是0，但是原码就有两种表示法：

 [-0]原=10000000

 [+0]原=00000000
复制代码

反码也有两种表示法：

 [+0]反=00000000

 [- 0]反=11111111
复制代码

这就有点难受啊，不都是0吗，于是乎，就出了补码

补码

那啥又是补码嘞？

负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1

比如：10000000 00000000 00000000 00000101 的反码是：11111111 11111111 11111111 11111010

那么，补码为：

11111111 11111111 11111111 11111010 + 1 = 11111111 11111111 11111111 11111011

这里有两点需要注意：

1、从补码求原码的方法跟原码求补码是一样的 ，也可以通过完全逆运算来做，先减一，再取反。

2、补码却规定0没有正负之分

第二个啥意思呢，也就是说对于0的表示，补码只有一种[-0]补=00000000。感觉这样就正常多了。

总结一下

原码表示法规定：用符号位（最左边）和数值表示带符号数，正数的符号位用“0”表示，负数的符号位用“1”表示，数值部分用二进制形式表示。

反码表示法规定：正数的反码与原码相同，负数的反码为对该数的原码除符号位外各位取反。

补码表示法规定：正数的补码与原码相同，负数的补码为对该数的原码除符号位外各位取反，然后在最后一位加1.

正零和负零的补码相同，[+0]补=[-0]补=0000 0000B

简单说说

其实你看，这些基础知识仔细研究起来，还是有一定难度的，觉得乱巴巴的，怪不得上大学的时候听不懂呢:joy:，而且这三个知识点貌似经常一起运用，所以对于这三点基础，还是有必要花时间琢磨一番的。

好啦，就到这了，欢迎大家一起讨论！

感谢阅读

大家好，我是ithuangqing，一路走来积累了不少的学习经验和方法，而且收集了大量的精品学习资源，现在维护了一个公众号【 编码之外 】，寓意就是在编码之外也要不停的学习，主要分享java技术相关的原创文章，现在主要在写 数据结构与算法，计算机基础，线程和并发以及虚拟机 这块的原创，另外针对小白还在连载一套《 小白的java自学课 》，力求通俗易懂，由浅入深。同时我也是个工具控，经常分享一些 高效率的黑科技工具及网站 。

对了，公众号还分享了很多我的学习心得，可以一起探讨探讨！

关注公众号，后台回复“庆哥”，2019最新java自学资源立马送上！更多原创精彩尽在【编码之外】

感谢各位大大的阅读