转载

浅谈序列化中的字节序

业务处理上，有时会直接对字节进行操作。例如:

实现私有协议 ，
对校验位进行检测 ，
敏感数据加密

基础概念

首先，我们需要理解几个基础概念。一般来说，字节是我们可以用语言处理的最小对象，无论是C/C++还是Java都没有直接提供bit类型。 1 byte = 8 bit ，除去最左侧的符号位1byte可以描述的范围是：-128 ~ 127。但是在大多数的业务处理中，我们通常会采用无符号位，即用1byte表示： 0 ~ 255 。其次，常见的移位操作符有左移（ << ）和右移（ >> ），比较容易忽视的是右移操作，如果最左侧的符号位为1则右移是在高位插入的是1。因此Java中增加了一种“无符号”右位移操作符 >>> ，通常用不上，了解即可。

最后，如果我们采用 byte[] 来表示一种数据类型，数组下标从小到大即内存地址的从低位到高位。记住这个概念非常重要，后面我会引入大端模式与小端模式。

为了让大家理解以上概念，下面看两个例子：

1. 假设 byte x = 127 ，对它执行左移1位的操作 x = ?

byte x = 127;
x <<= 1;
System.out.println(Integer.toHexString(x));
复制代码

在代码执行之前我们先使用计算器计算一下： BIN(1111 1110) HEX(FE) ，代码的执行结果为： FFFFFFFE 。原因是对x左移1位超出了byte的表示范围，Java自动在左侧补位，由于最高位是1，因此我们获得了一个怪异的结果。那么有什么办法得到一个正确的结果呢？

byte x = 127;
x <<= 1;
System.out.println(Integer.toHexString(x & 0xFF));
复制代码

1. 假设 byte x = 1 ，对它执行左移32位的操作 x = ?

byte x = 1;
System.out.println(x << 32);
复制代码

答案是1。这个结论比较怪异而且确实是一个坑，大家只需要记住：对一个int值来说，左移32位等于它的原始值；对于一个long值来说，左移64位等于它的原始值。

在理解了这些基本概念以后，我们已经做好了进入字节世界的准备。

何为大端序，小端序？

简单点说，就是字节的存储顺序，如果数据都是单字节的，那怎么存储无所谓了，但是对于多字节数据，比如int，double等，就要考虑存储的顺序了。注意字节序是硬件层面的东西，对于软件来说通常是透明的。再说白一点，字节序通常只和你使用的处理器架构有关，而和编程语言无关，比如常见的Intel x86系列就是小端序。

Big-endian（大端序）

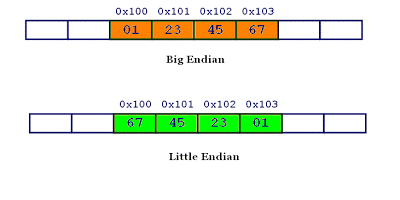
数据的高位字节存放在地址的低端低位字节存放在地址高端

Little-endian（小端序）

数据的高位字节存放在地址的高端低位字节存放在地址低端

同理， 0x1234567 的大端字节序和小端字节序的写法如下图。

为什么会有小端字节序？

答案是，计算机电路先处理低位字节，效率比较高，因为计算都是从低位开始的。所以，计算机的内部处理都是小端字节序。

但是，人类还是习惯读写大端字节序。所以， 除了计算机的内部处理，其他的场合几乎都是大端字节序 ，比如网络传输和文件储存。

我们如何用4个字节的大端模式表示一个整型变量？

用途

通常用于序列化的时候，写入到字节流。

而对于byte[4]来说，bs[0]即为地址高位，bs[3]即为地址低位。这样看来就很清楚了。大端模式符合人们的阅读模式。大端模式，高位在左边：[byte[0],byte[1],byte[3],byte[4]]。

int i = 0x1234;
byte[] bs = new byte[4];
bs[0] = (byte) (i >> 24 & 0xFF); // 右移3字节，获取高1字节，& 0xFF
bs[2] = (byte) (i >> 16 & 0xFF);
bs[3] = (byte) (i >> 8 & 0xFF);
bs[4] = (byte) (i & 0xFF);

for(byte b : bs) {
    System.out.println(Integer.toHexString(b));
}
复制代码

更抽象的算法，大家可以在理解了上面的例子以后自己封装。

反过来

我们将以大端模式生成的4个字节还原为一个整型数？

用途通常用于反序列化的时候，从字节流解析出来。

举例来说，处理器读入一个16位整数。如果是大端字节序，就按下面的方式转成值。

x = buf[offset] * 256 + buf[offset+1];
复制代码

上面代码中，buf是整个数据块在内存中的起始地址，offset是当前正在读取的位置。第一个字节乘以256，再加上第二个字节，就是大端字节序的值，这个式子可以用逻辑运算符改写。

x = buf[offset]<<8 | buf[offset+1];
复制代码

上面代码中，第一个字节左移8位（即后面添8个0），然后再与第二个字节进行或运算。

如果是小端字节序，用下面的公式转成值。

x = buf[offset+1] * 256 + buf[offset];
复制代码

32位整数的求值公式也是一样的。

/* 大端字节序 */
i = (data[0]<<24) | (data[1]<<16) | (data[2]<<8) | (data[3]<<0) ;

/* 小端字节序 */
i = (data[0]<<0) | (data[1]<<8) | (data[2]<<16) | (data[3]<<24);
复制代码

4个字节还原为一个整型数就很容易了

int x = （bs[3] & 0xFF）; // 获取低1字节
x |= （bs[2] & 0xFF） << 8;  // 获取低2字节
x |= （bs[1] & 0xFF） << 16;// 获取低3字节
x |= （bs[0] & 0xFF） << 24; // 获取低4字节

System.out.println(Integer.toHexString(x));
复制代码

注意：为了得到正确的结果，我们在对byte进行移位前一定要先做位与（&）操作。

接下来我们需要升级问题，将一个8个字节宽度的符合大端模式的字节数组还原为一个长整型数。

long x = bs[7] & 0xFF;
x |= (bs[6] & 0xFF) << 8;
x |= (bs[5] & 0xFF) << 16;
x |= (bs[4] & 0xFF) << 24;
x |= (bs[3] & 0xFF) << 32;
x |= (bs[2] & 0xFF) << 40;
x |= (bs[1] & 0xFF) << 48;
x |= (bs[0] & 0xFF) << 56;
System.out.println(Long.toHexString(x));
复制代码

似乎我们很容易按照整型的转换方式得到以上算法。不幸的是，这样做是错误的。如果这个byte[]表示的数字范围超过整型数的上限，我们将无法获得正确的长整型数。原因是Java默认在对byte进行移位操作前会转换为int类型，还记得上面我们让大家记住“对一个int值来说，左移32位等于它的原始值”吗？正确的做法应该是这样：

long x = bs[7] & 0xFF;
x |= ((long)bs[6] & 0xFF) << 8;
x |= ((long)bs[5] & 0xFF) << 16;
x |= ((long)bs[4] & 0xFF) << 24;
x |= ((long)bs[3] & 0xFF) << 32;
x |= ((long)bs[2] & 0xFF) << 40;
x |= ((long)bs[1] & 0xFF) << 48;
x |= ((long)bs[0] & 0xFF) << 56;
System.out.println(Long.toHexString(x));
复制代码

至此我们应该可以很轻松的解决有关字节转换的各种难题了，但是上面的这些算法未免显得太不优美，幸亏Java早就为我们想到了这一点。本着不要重复造轮子的观点，我提供了一套工具。

/**
 * 任意字节宽度转换为标准整型数
 */
public static int bytesToInt(byte[] bytes, int byteNum, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(4);
    buffer.order(order);
    buffer.put(bytes, 0, bytes.length);
    buffer.put(new byte[buffer.limit() - byteNum], 0, buffer.limit() - byteNum);
    buffer.flip();
    return buffer.getInt();
}

/**
 * 长整型数转换为指定字节宽度
 */
public static byte[] longToBytes(long x, int byteNum, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(8);
    buffer.order(order);
    buffer.putLong(0, x);
    return Arrays.copyOfRange(buffer.array(), 0, byteNum);
}

/**
 * 任意字节宽度转换为长整型
 */
public static long bytesToLong(byte[] bytes, int byteNum, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(8);
    buffer.order(order);
    buffer.put(bytes, 0, bytes.length);
    buffer.put(new byte[buffer.limit() - byteNum], 0, buffer.limit() - byteNum);
    buffer.flip();
    return buffer.getLong();
}

/**
 * 长整型数转换为标准的8字节宽度
 */
public static byte[] longToBytes(long x, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(8);
    buffer.order(order);
    buffer.putLong(0, x);
    return buffer.array();
}

/**
 * 标准8字节宽度转换为长整型数
 */
public static long bytesToLong(byte[] bytes, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(8);
    buffer.order(order);
    buffer.put(bytes, 0, bytes.length);
    buffer.flip();
    return buffer.getLong();
}

/**
 * 整型数转换为标准4字节宽度
 */
public static byte[] intToBytes(int x, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(4);
    buffer.order(order);
    buffer.putInt(0, x);
    return buffer.array();
}

/**
 * 标准4字节宽度转换为整型数
 */
public static int bytesToInt(byte[] bytes, ByteOrder order) {
    ByteBuffer buffer = ByteBuffer.allocate(4);
    buffer.order(order);
    buffer.put(bytes, 0, bytes.length);
    buffer.flip();
    return buffer.getInt();
}
复制代码

参考： www.ruanyifeng.com/blog/2016/1…

原文 https://juejin.im/post/5e23336ee51d454d7a2598de

正文到此结束