转载

Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

Map 在 Java Collections Framework 中设计相关知识点比较多的数据结构，无论是工作还是面试中都会被频繁的涉及到。通过学习 Map 的源码，我们能够深入理解相当部分的数据结构知识和编码技巧。在接下来的几篇文章中会介绍一些数据结构的知识，希望大家不会觉得无聊，因为这部分的能力才是作为程序员的核心能力。同时这部分的知识其实也不是那么高深，我会试着用最简单明了的方法帮你理解。

Map 接口

Map 数据结构的特点很明显，允许我们使用 key 来存储和读取元素，并且不允许重复的 key。而不同 Map 的实现对于 key 的顺序处理是不一致的。例如 HashMap 无法保证 key 的顺序，而 TreeMap 则是按照 key 实现的 Comparator 接口方法来确定顺序的。

Map 上也定义了每一个 key-value 对应的数据必须实现 Entry 接口，上面定义的方法也很简单，基本都是对于 key 和 value 的操作。

Map 接口上定义的方法，大家应该都比较熟悉，我这里就不啰嗦了。特别会提及在 JDK8 加入的几个方法，在日常工作中比较实用。如果之前没有 JDK8 使用经验的，可以了解一下。

* `getOrDefalut(Object key, V defaultValue)`：当 `Map` 中有 key 对应的 value 时返回 `Map` 中的 value， 否则返回 `defaultValue` 。
* `V compute(K key,BiFunction<? super K, ? super V, ? extends V> remappingFunction)`：将 `Map` 中的 key 和对应的 value 作为参数，调用 `remappingFunction` 方法获得 newValue，如果 newValue 不为 null，则替换原来的 value。
* `V putIfAbsent(K key, V value)`：如果当前 `Map` 中没有 key 对应的 value，则执行 put 操作。
* `V merge(K key, V value, BiFunction<? super V, ? super V, ? extends V> remappingFunction)`：如果当前没有 key 对应的 value，则将参数 value 放入 `Map` 中，否则将原来 key 对应的 value 和新的 value 作为参数调用 `remappingFunction` ，将结果 put 入 `Map` 中。

这些方法的实现都在 Map 接口中，使用的 JDK8 新增的 default 关键字以保持向下兼容，具体的代码非常简单，这里就不啰嗦了。

TreeMap

相对 HashMap 而言， TreeMap 涉及的知识点更少些，适合作为熟悉 Map 数据结构的敲门砖。先来看看它的类图：

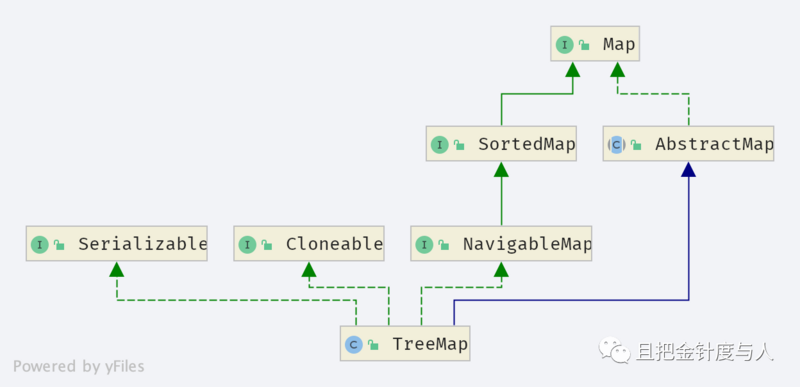
Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

可以看到 TreeMap 继承了 AbstractMap ，并实现了 NavigableMap 接口。 AbstractMap 上提供了部分模版方法，便于开发人员实现自己的 Map ，而 NavigableMap 提供了类似之前提及的 NavigableSet 的那些方法，能够返回某个范围的 key 或是 value。所以我们直接来看 TreeMap 的具体实现细节。

从一开头的注释中可以得知， TreeMap 是通过红黑树这一数据结构实现的，因此它能够保证 containsKey ， get ， put ， remove 的时间复杂度为 log(n) 。而同样的， TreeMap 也不是线程安全的。所以真正理解 TreeMap 的关键在于了解和掌握红黑树的这一数据结构。所以接下来的部分，我先会花些篇幅帮助你复习一下红黑树的特性，不要觉得这是个很难任务，我保证你看完系列文章后一定能够用 Java 手写红黑树。

平衡二叉树

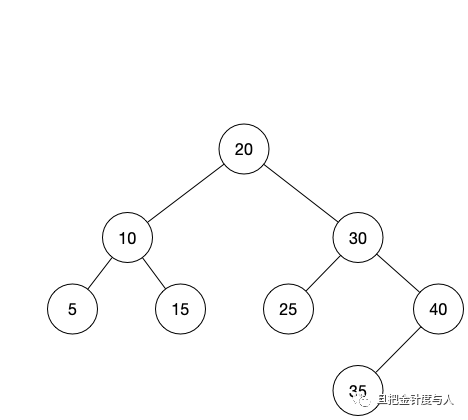
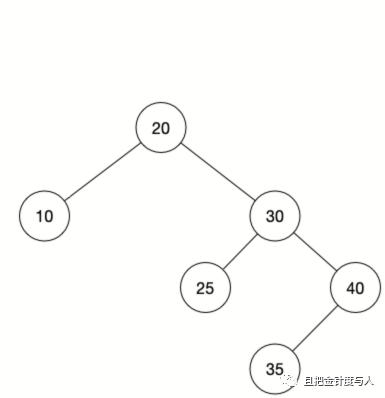
用一句话来说红黑树是一种 平衡二叉树 。二叉树的概念大家应该都知道，即每个父节点拥有不超过两个子节点的树。而平衡的意思是左右子树的高度相差不超过一。同时所有左边子树的值都比当前节点小，而右边子树的值都比当前节点大。我们来看一下几个例子。

可以看到图1是一棵平衡二叉树，符合我们之前提到的条件，但是图2就不符合了，因为左右子树的高度相差超过了一。

Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

维持平衡的目的在于不让二叉树退化为链表，这样就可以进行二分查找，保持查找的时间复杂度为 log(n) 。但这也意味着在增加节点或是移除节点的时候需要做特殊的操作，以保持整个二叉树的平衡，而红黑树就是这样的一种数据结构。

红黑树

像之前提及的，红黑树本身是一种平衡二叉树，因此它具备平衡二叉树的所有特点。在此基础上它有一些自己特有的约束条件与特性。

红黑树的每个节点额外增加了一个颜色的特性，即红色，或是黑色，只能是这两个中的一种，这也是它红黑树名称的由来。我们看一下 TreeMap 中红黑树节点的源码：

static final class Entry<K,V> implements Map.Entry<K,V> {
    K key;
    V value;
    Entry<K,V> left;
    Entry<K,V> right;
    Entry<K,V> parent;
    boolean color = BLACK;
}

TreeMap 中每个节点实现了 Map 中的 Entry 接口，除了代表当前节点的 key，value 两个数据项，还有代码自身节点下的左右子节点的 left 和 right ，以及自己父节点的 parent 。最后就是代表当前节点颜色的 color ，这里的定义同样在 TreeMap 的源码中：

private static final boolean RED   = false;
private static final boolean BLACK = true;

接着我们看一下红黑树的特性：

* 根节点(root node) 的颜色始终为黑色
* 两个相邻的节点(即连接在一起的节点)不能同为红色
* 从根节点出发，到某个子节点的每条路径上的黑色节点数量都相同

怎么样？够简单吧！接着让我们看个例子。

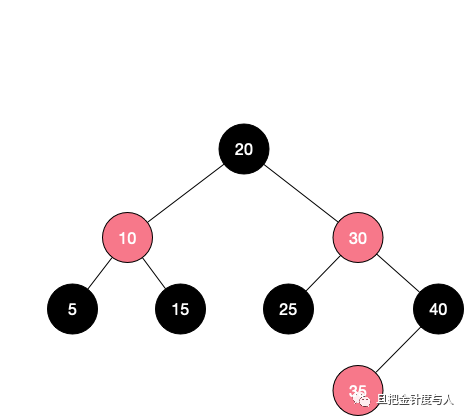
Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

从上面的图来看符合我们之前列出的 3 个特性，请验证一下确保自己对红黑树的概念理解正确。

红黑树的三个基本操作

通过上面的描述你应该已经掌握了红黑树的概念，知道什么是红黑树了。在介绍红黑树的插入以及删除操作之前，我们先学习三个基本的操作，即颜色变化(color flip)，左旋转(left rotation) 和右旋转(right rotation)。

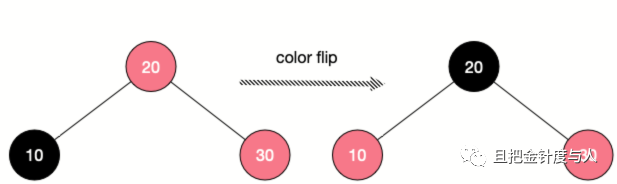
颜色变化

非常简单，将当前节点颜色变为红色，左右两个子节点的颜色都变为黑色。入下图所示。

Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

左旋转与右旋转

用语言来描述可能有些抽象，我们还是看一下图片示例，该图片来自 wikipedia。

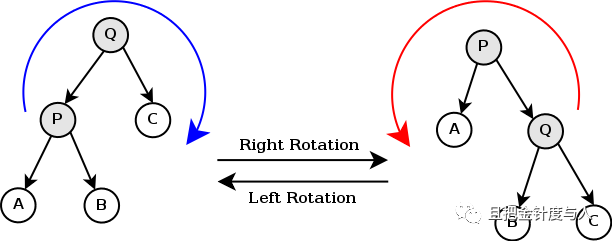
Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)

请多看几遍这幅图，确保自己了解左旋转和右旋转的意义，因为这三个基本操作是后续红黑树插入和删除操作的基础。

结语

这次主要介绍了 Map 和 TreeMap 的一些基础功能，和 TreeMap 之下红黑树的基本概念。红黑树是一种比较重要的高级数据结构，对于开发人员来说应该是熟练掌握的，本次主要介绍了基本概念和基础的操作。下一篇我们会涉及红黑树的的插入以及删除操作的具体算法，在进入这部分前，我再次强调请熟练掌握本文的内容，因为这是基础中的基础。

下一篇文章中我会对照 TreeMap 的源码介绍红黑树的算法，希望你不要错过！

欢迎关注我的微信号「且把金针度与人」,获取更多高质量文章

Java Collections Framework 源码分析(5.1 - Map, TreeMap, 红黑树)