排序算法(Java)
排序算法在算法中占有重要地位,我实在太菜,记性也不大好,先记录一下吧。
本文记录了十大排序算法,很多文章都是八大算法,桶排序、计数排序和基数排序也很重要,所以都记录下来。
2. 概述
排序算法分为 内部排序 和 外部排序 ,内部排序把数据记录放在内存中进行排序,而外部排序因排序的数据量大,内存不能一次容纳全部的排序记录,所以在排序过程中需要访问外存。
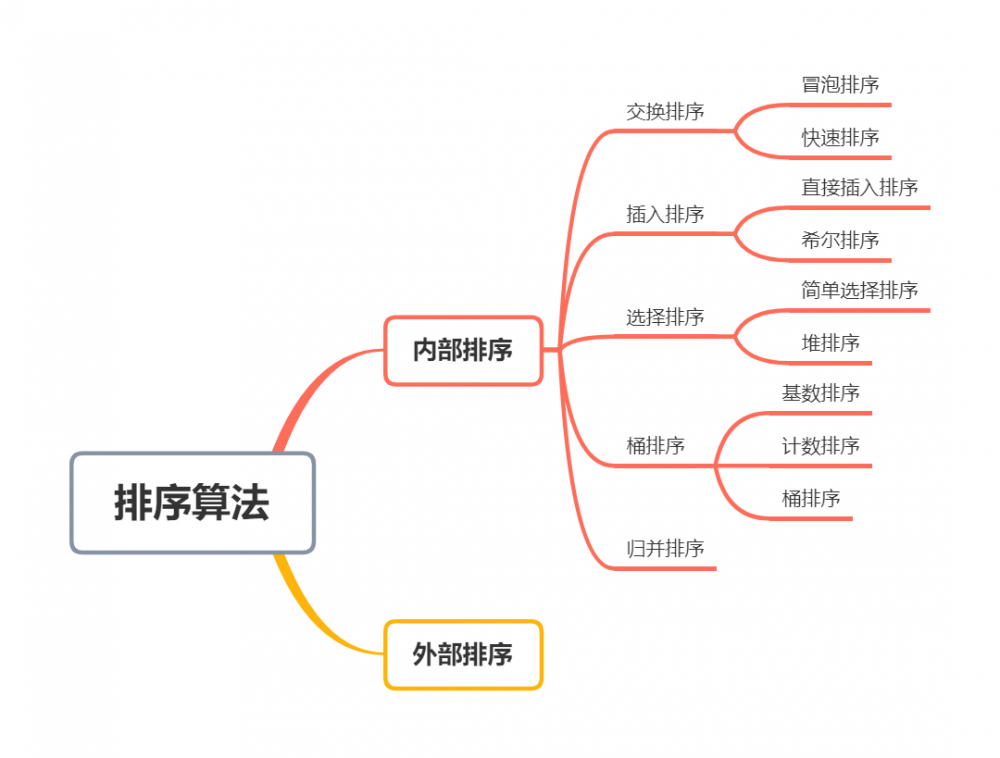
我将基数排序、计数排序、桶排序三个归为一类,因为都采用了桶思想。
这儿说一下 术语
- 稳定 :如果a原本在b前面,而a=b,排序之后a仍然在b的前面
- 不稳定 :如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面
- 时间复杂度: 一个算法执行所耗费的时间
- 空间复杂度 :运行完一个程序所需内存的大小
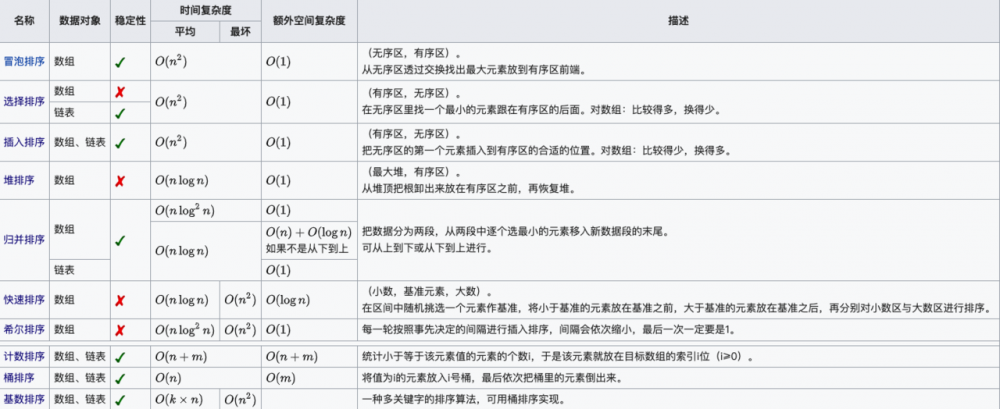
讲算法的文章实在太多了,我仅仅记录一下几个算法。详细讲解参考 十大经典排序算法
3. 算法
排序里面很多地方都要用到交换,先把交换写一下
public static void swap(int[] arr, int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
}
复制代码
冒泡排序
//冒泡排序
public static void bubbleSort(int[] arr) {
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) swap(arr, j, j + 1);
}
}
}
复制代码
快速排序
//快速排序
public static void quickSort(int[] nums, int head, int end) {
if (nums.length == 0 || head >= end || end == 0) return;
int key = nums[head], i = head, j = end;
while (i <= j) {
while (nums[i] < key) {
++i;
}
while (nums[j] > key) {
--j;
}
if (i < j) {
swap(nums, i, j);
++i;
--j;
} else if (i == j) {
++i;
}
}
quickSort(nums, head, j);
quickSort(nums, i, end);
}
复制代码
插入排序
//插入排序
public static void insertSort(int[] nums) {
for (int i = 1; i < nums.length; i++) {
for (int j = i; j > 0; j--) {
if (nums[j] < nums[j - 1]) {
swap(nums, j, j - 1);
}
}
}
}
复制代码
希尔排序
//希尔排序
public static void shellSort(int[] arr) {
//Knuth序列--提高效率
int h = 1;
while (h <= arr.length / 3) {
h = 3 * h + 1;
}
for (int gap = h; gap > 0; gap = (gap - 1) / 3) {
for (int i = gap; i < arr.length; i++) {
for (int j = i; j > gap - 1; j -= gap) {
if (arr[j] < arr[j - gap]) {
swap(arr, j, j - gap);
}
}
}
}
}
复制代码
选择排序
//选择排序
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
int index = i;
for (int j = i; j < arr.length; j++) {
if (arr[index] > arr[j]) index = j;
}
if (index != i) {
swap(arr, i, index);
}
}
}
复制代码
堆排序
//堆排序
public static void heapSort(int[] arr) {
/*
* 第一步:将数组堆化
* beginIndex = 第一个非叶子节点。
* 从第一个非叶子节点开始即可。无需从最后一个叶子节点开始。
* 叶子节点可以看作已符合堆要求的节点,根节点就是它自己且自己以下值为最大。
*/
int len = arr.length;
int parent = (len >> 1) - 1;
for (int i = parent; i >= 0; i--)
heapify(arr, i, len - 1);
maxHeap(arr, len);
}
/**
* 第二步:对堆化数据排序
* 每次都是移出最顶层的根节点A[0],与最尾部节点位置调换,同时遍历长度 - 1。
* 然后从新整理被换到根节点的末尾元素,使其符合堆的特性。
* 直至未排序的堆长度为 0。
*/
public static void maxHeap(int[] arr, int len) {
for (int i = len - 1; i > 0; i--) {
swap(arr, 0, i);
heapify(arr, 0, i - 1);
}
}
/**
* 调整索引为 index 处的数据,使其符合堆的特性。
*
* @param index 需要堆化处理的数据的索引
* @param len 未排序的堆(数组)的长度
*/
public static void heapify(int[] arr, int index, int len) {
int left_child = (index << 1) + 1; // 左子节点索引
int right_child = left_child + 1; // 右子节点索引
int maxIndex = left_child; // 子节点值最大索引,默认左子节点。
if (left_child > len) return; // 左子节点索引超出计算范围,直接返回。
if (right_child <= len && arr[right_child] > arr[left_child]) // 先判断左右子节点,哪个较大。
maxIndex = right_child;
if (arr[maxIndex] > arr[index]) {
swap(arr, maxIndex, index); // 如果父节点被子节点调换,
heapify(arr, maxIndex, len); // 则需要继续判断换下后的父节点是否符合堆的特性。
}
}
复制代码
基数排序
//基数排序
public static void radixSort(int[] arr) {
int[] temp = Arrays.copyOf(arr,arr.length);
//int[] res = new int[arr.length];
int[] count = new int[10];
int numLen = getNumLength(getMax(arr));
for (int i = 0; i < numLen; i++) {
//统计各个桶将要装入的数据个数
int division = (int) Math.pow(10, i);
for (int value : temp) {
int num = value / division % 10;
count[num]++;
}
// count[m]表示第m个桶的右边界索引
for (int m = 1; m < count.length; m++) {
count[m] += count[m - 1];
}
// 将数据依次装入桶中
// 这里要从右向左扫描,保证排序稳定性
for (int k = temp.length - 1; k >= 0; k--) {
int num = temp[k] / division % 10;
// 对应桶的装入数据索引减一
count[num]--;
// 求出关键码的第k位的数字, 例如:576的第3位是5
arr[count[num]] = temp[k];
}
temp = Arrays.copyOf(arr,arr.length);
Arrays.fill(count, 0);
}
}
//获取数组最大值
public static int getMax(int[] arr) {
int len = arr.length;
if (len == 0) return 0;
int max = 0;
for (int i = 1; i < len; i++) {
if (arr[max] < arr[i]) {
max = i;
}
}
return arr[max];
}
//获取数字的位数
public static int getNumLength(int num) {
if (num == 0) return 1;
int len = 0;
for (int i = num; i > 0; i /= 10) {
len++;
}
return len;
}
复制代码
计数排序
public static void countSort(int[] arr) {
int max = arr[0], min = arr[0];
int[] temp = Arrays.copyOf(arr,arr.length);
for (int value : arr) {
if (max < value) max = value;
if (min > value) min = value;
}
int[] count = new int[max - min + 1];//节省空间
for (int i : arr){
count[i - min]++;
}
for (int j = 1;j < count.length;j++){
count[j] += count[j - 1];
}
for (int m = temp.length-1;m >= 0;m--){
arr[--count[temp[m]-min]] = temp[m];
}
}
复制代码
桶排序
public static void bucketSort(int[] arr) {
int max = arr[0], min = arr[0];
for (int a : arr) {
if (max < a)
max = a;
if (min > a)
min = a;
}
//桶数量
int bucketNum = max / 10 - min / 10 + 1;
List<List<Integer>> buckList = new ArrayList<>();
// create bucket
for (int i = 1; i <= bucketNum; i++) {
buckList.add(new ArrayList<>());
}
// push into the bucket
for (int value : arr) {
int index = indexFor(value, min, 10);
buckList.get(index).add(value);
}
ArrayList<Integer> bucket = null;
int index = 0;
for (int i = 0; i < bucketNum; i++) {
bucket = (ArrayList<Integer>) buckList.get(i);
insertSort(bucket);
for (int k : bucket) {
arr[index++] = k;
}
}
}
//确定数字属于的桶的索引
private static int indexFor(int a, int min, int step) {
return (a - min) / step;
}
复制代码
归并排序
//归并排序
public static void mergeSort(int[] nums, int low, int high) {
if (low >= high) {
return;
}
int mid = low + ((high - low) >> 1);
mergeSort(nums, low, mid);
mergeSort(nums, mid + 1, high);
merge(nums, low, mid, high);
}
public static void merge(int[] nums, int low, int mid, int high) {
int[] temp = new int[high - low + 1];
int key = 0;
int p1 = low, p2 = mid + 1;
while (p1 <= mid && p2 <= high) {
temp[key++] = nums[p1] <= nums[p2] ? nums[p1++] : nums[p2++];
}
while (p1 <= mid) {
temp[key++] = nums[p1++];
}
while (p2 <= high) {
temp[key++] = nums[p2++];
}
for (int value : temp) {
nums[low++] = value;
}
}
复制代码
参考资料
- 十大经典排序算法最强总结(含JAVA代码实现)
- 面试必备:八种排序算法原理及Java实现
- 八大排序算法总结与java实现
正文到此结束
热门推荐
相关文章
Loading...











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

