一篇文章让你了解二分搜索树的数据结构的实现过程(Java 实现)
目录
树结构简介
- 在线性数据结构中,数据都是排成一排存放的;而树结构则是非线性的,存储在其中的数据是按分支关系组织起来的结构,就像自然界中的树那样。如下图所示:
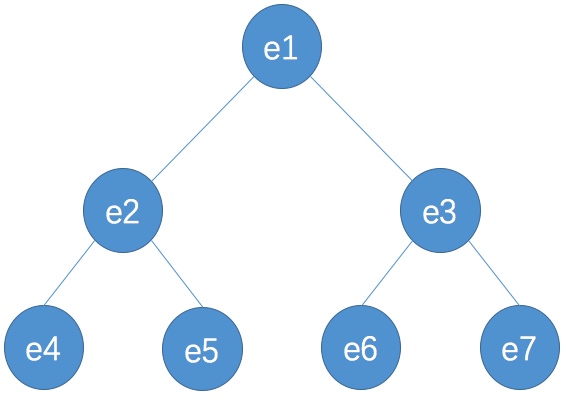
- 从图可以看出树结构是有一种层次感的,每一个点可以有多个分支,这种组织结构是非常有优势的,简单来说树结构本身是一种天然的组织结构。
- 对于这种组织结构,日常生活中是非常常见的,比如电脑磁盘中的文件夹、公司中的人员组织结构、家族的族谱等等,如以下几图所示:
- 除了组织数据,使用树结构存储数据时,在某些情况下,处理数据是十分高效的。而我们就可以针对各种特殊情况去设计出各情况适合的高效率的树结构。
- 举个例子:比如对于查找一个数据,在线性结构中如果不知道具体位置的话需要在一堆数据里一个一个地去寻找;而对于树结构,因为树结构分支的形式,各个数据可以存在不同的分支中,在查找时就可以依据这些分支快速地找到想要的数据。
- 比如,磁盘中不同的文件夹存放不同的文件,我们在查找一个文件时,就可以根据文件夹名称去找到想要的文件。
- 以上就是树结构的一些特点的简单介绍,接下来就开始分析一下树结构中的二分搜索树的基础知识以及实现出这个数据结构的一些常用操作。
二分搜索树的基础知识
二叉树的基本概念
- 在了解二分搜索树之前,需要先了解二叉树的基本概念,因为二分搜索树是基于二叉树的。实际上,二叉树是树结构中最常见的树结构,也是树结构中最为基础的结构。
- 对于二叉树,和链表一样,也是一种动态的数据结构,用户不需要担心容量的问题,设计者也不需要手动地设计动态伸缩容量的方法。
- 同时,二叉树也是由一个一个节点组成的,而对于其中的每一个节点,除了存储数据之外,还需要有两个子节点,分别指向这个节点的左节点和右节点(也称为左孩子和右孩子)。
- 此外,二叉树还具有以下特性:
- 二叉树具有唯一根节点。
- 二叉树每个节点最多有两个孩子。
- 二叉树中没有孩子的节点称为叶子节点。
- 二叉树每个节点最多只有一个父亲节点。
- 二叉树具有天然的递归结构:
- 每个节点的左子树也是二叉树。(每个节点的左节点是左子树的根节点)
- 每个节点的右子树也是二叉树。(每个节点的右节点是右子树的根节点)
- 二叉树不一定是满的:
- 一个节点也是二叉树。(左右孩子为空)
- NULL(空)也是二叉树。
- 以上特性归纳为图片表示如下:
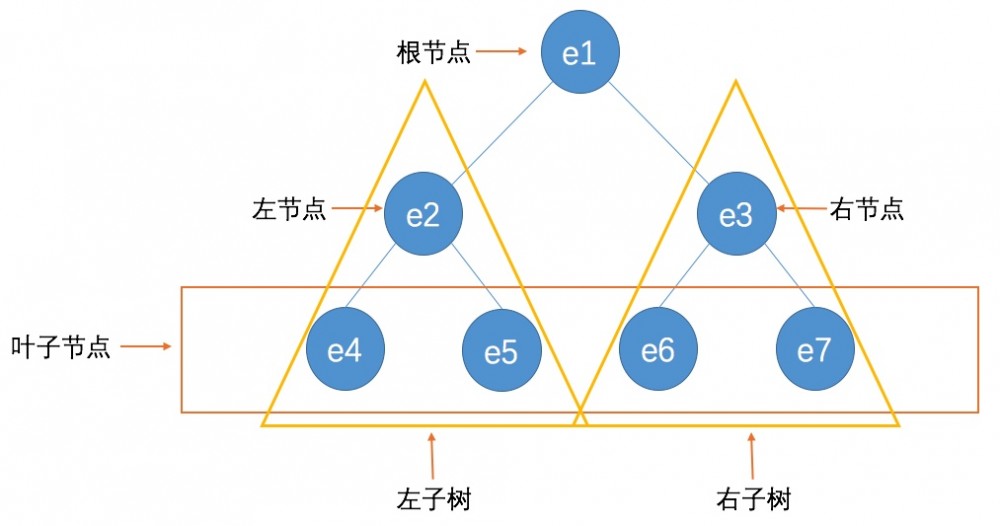
- 二叉树的几种常见形态
- 空二叉树
- 只有一个节点的二叉树

- 只有左节点的二叉树

- 只有右节点的二叉树
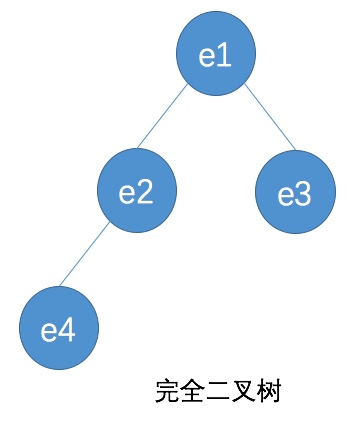
- 完全二叉树
- 满二叉树
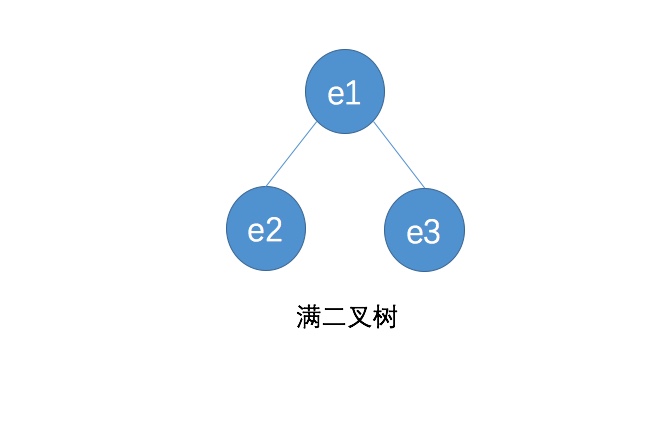
- 空二叉树
二分搜索树的基本概念
- 在了解了以上二叉树的基本概念之后,那么对于二分搜索树就不需要再了解以上概念了,因为二分搜索树就是一棵二叉树,只不过它有属于它自己的一些特性。
- 对于二分搜索树,它具有以下特性:
- 二分搜索树的每个节点的值大于其左子树的所有节点的值。
- 二分搜索树的每个节点的值小于其右子树的所有节点的值。
- 二分搜索树的每一棵子树也是二分搜索树。
- 二分搜索树存储的元素必须有可比较性。
- 二分搜索树图示
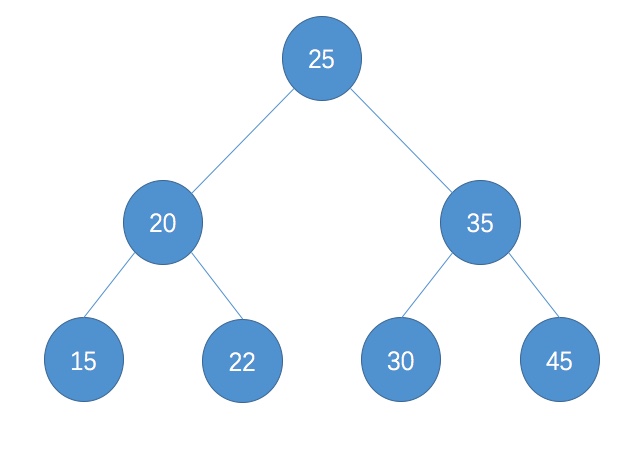
二分搜索树的基本结构代码实现
-
综上以上基本概念,可设计二分搜索树的基本结构的代码如下:
/** * 二分搜索树数据结构实现类 * 支持具有可比较性的泛型 * * @author 踏雪彡寻梅 * @date 2020/3/2 - 23:05 */ public class BST<E extends Comparable<E>> { /** * 二分搜索树的节点 */ private class Node { /** * 存储在节点中的元素 */ public E element; /** * 左节点(左孩子) */ public Node left; /** * 右节点(右孩子) */ public Node right; /** * 节点类构造函数 * 构造一个没有左右孩子的节点 * @param element 存储在节点中的元素 */ public Node(E element) { this.element = element; this.left = null; this.right = null; } } /** * 二分搜索树的根节点 */ private Node root; /** * 二分搜索树当前节点个数 */ private int size; /** * 二分搜索树类构造函数 * 构造一个空的二分搜索树 */ public BST() { this.root = null; this.size = 0; } /** * 获取二分搜索树当前节点个数 * @return 返回当前二分搜索树中节点个数 */ public int size() { return size; } /** * 判断当前二分搜索树是否为空树 * @return 返回 true,表示当前二分搜索树为空树;返回 false,表示当前二分搜索树不为空树 */ public boolean isEmpty() { // 判断 size 是否为 0 即可 return size == 0; } }
二分搜索树的常见基本操作实现
添加操作
添加操作初步实现
-
对于二分搜索树的添加操作,可分为以下两种情况(为了更加简洁明了,此处使用动图表示):
- 空树时添加一个新元素:

- 树中已有元素时添加新元素:
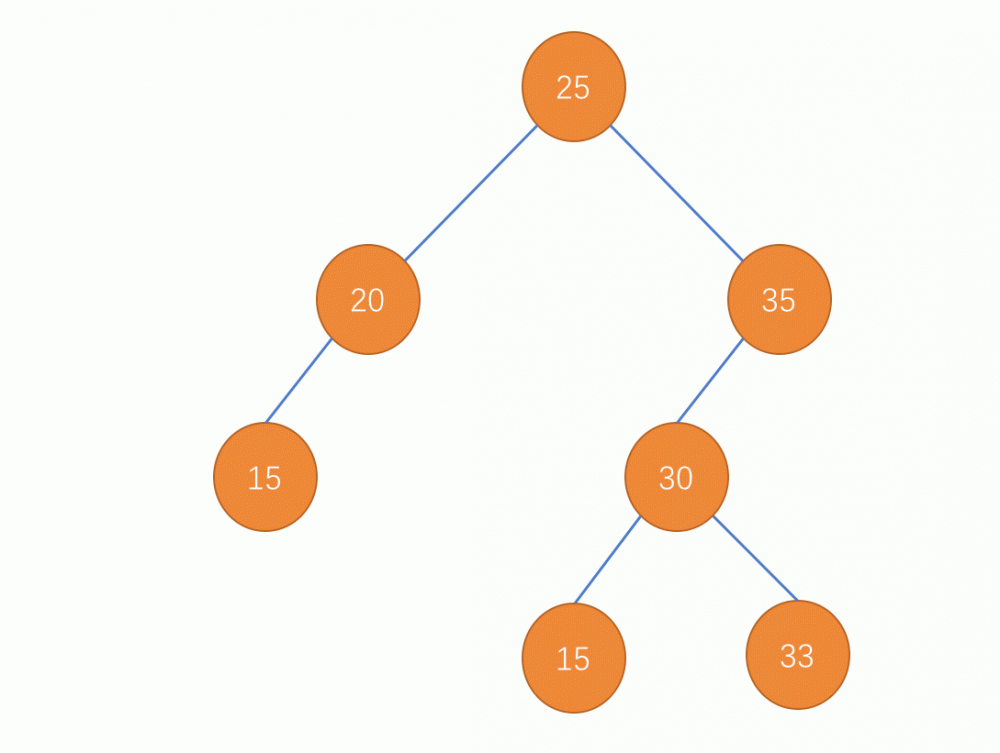
- 空树时添加一个新元素:
-
以上就是添加元素的过程,其中需要注意的是在这里的二分搜索树的实现中,不包含重复元素,如果添加的元素已有了直接返回忽略。
-
如果需要包含重复元素,只需要定义为:左子树小于等于父节点,右子树大于等于父节点。
-
对于其代码实现,可以使用非递归方式也可以使用递归方式,对于非递归方式,实现步骤其实和链表比较相像;但是在树结构中,递归实现是比非递归方式简单的,所以在这里使用递归的方式来实现。
-
不过使用递归方式也是有一定的局限性的。比如在添加元素的最坏的情况下,二分搜索树会形成一个链表(只添加左节点或右节点),这种情况下一直添加元素,由于不断地递归,递归高度越来越高,内存将会被撑爆,这一点也是需要了解的。
-
从以上图示中,可归纳为以下步骤(递归实现):
- 添加元素前,先判断当前二分搜索树是否为空。如果为空将元素添加到根节点中;如果不为空,从根节点开始,递归将元素添加到树中。
- 递归终止条件:
- 添加的元素在树中已有,直接忽略掉返回即可。(不包含重复元素)
- 如果添加的元素添加到某个节点的左节点中且当前这个节点的左节点为空,则将元素添加到当前这个节点的左节点中并返回回去。
- 如果添加的元素添加到某个节点的右节点中且当前这个节点的右节点为空,则将元素添加到当前这个节点的右节点中并返回回去。
- 如果不满足以上终止条件,进行递归添加元素:
- 如果添加的元素比当前节点的元素小,添加到当前节点的左子树中。
- 如果添加的元素比当前节点的元素大,添加到当前节点的右子树中。
-
以上步骤实现为代码形式如下:
/** * 向二分搜索树中添加新的元素 element * @param element 添加的新元素 */ public void add(E element) { // 判断二分搜索树是否为空 if (root == null) { // 二分搜索树为空,将新元素添加到根节点中 root = new Node(element); size++; } else { // 二分搜索树不为空,从根节点开始递归地添加新元素 add(root, element); } } /** * 向根节点为 node 的二分搜索树中添加元素 element * 递归函数 * @param node 添加元素的二分搜索树的根节点 * @param element 添加的元素 */ private void add(Node node, E element) { // 终止条件 if (node.element.equals(element)) { // 添加的元素已有,忽略返回 return; } else if (element.compareTo(node.element) < 0 && node.left == null) { // 添加的元素添加到某个节点的左节点时(该节点的左节点为空) node.left = new Node(element); size++; return; } else if (element.compareTo(node.element) > 0 && node.right == null) { // 添加的元素添加到某个节点的右节点时(该节点的右节点为空) node.right = new Node(element); size++; return; } // 不满足终止条件时,递归的进行添加元素 if (element.compareTo(node.element) < 0) { // 比当前节点小,添加到左子树中 add(node.left, element); } else { // 比当前节点大,添加到右子树中 add(node.right, element); } }
添加操作改进
-
在上面的添加操作实现中,在添加新元素的时候进行了两轮的比较,第一轮是在终止条件时比较,第二轮是不满足终止条件时比较,这样子看起来终止条件显得比较臃肿。
-
而对于二叉树而言,空(null)也可以是一颗二叉树。所以可以设计为添加元素时当递归到某个节点的左节点或右节点时或者树为空时添加元素时,这个节点正好为空(null),此时就可以 new 一个节点将元素添加进去并返回这个节点给上一层的二分搜索树的左节点或右节点接收或者给根节点 root 接收,此时返回的这个节点就是一棵二分搜索树同时也是这棵树的根节点,对于相等的元素则不做处理,最后再返回递归最开始的根节点回去给上层节点或者根节点 root 接收即可。
-
此时在初始调用添加操作时,就不需要再判断二分搜索树是否为空了,只需使用 root 接收调用结果即可。
-
以上过程用动图表示如下:
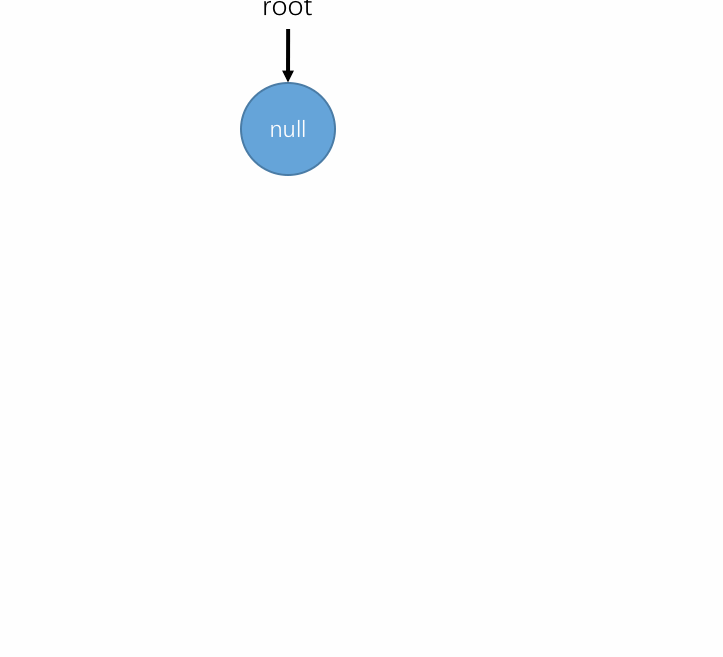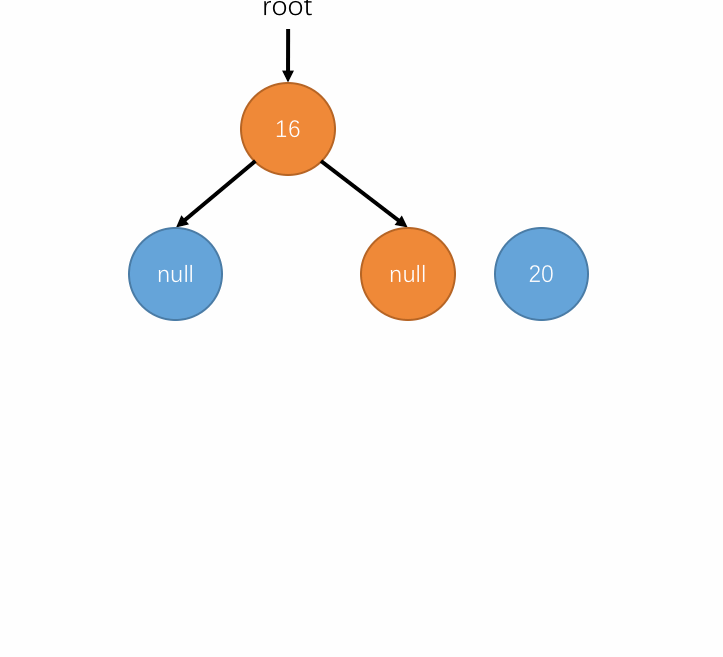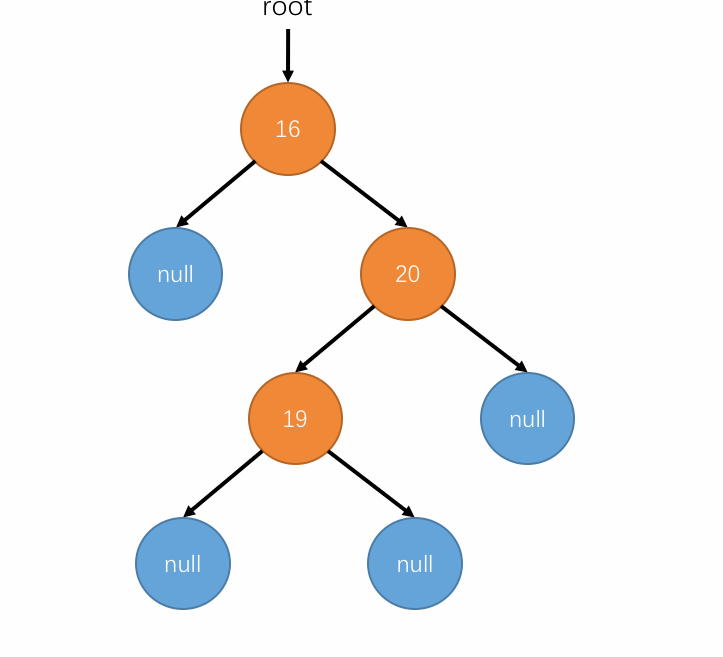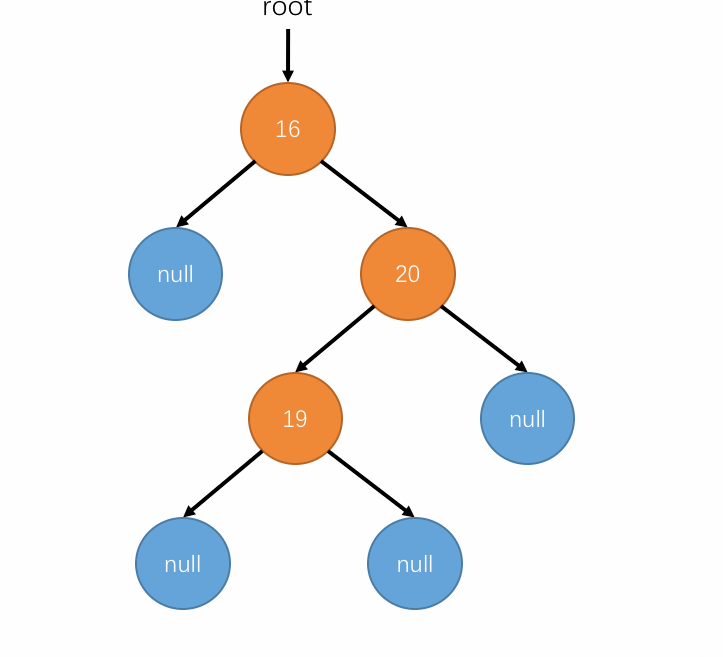
-
代码改进后如下:
/** * 向二分搜索树中添加新的元素 element * @param element 添加的新元素 */ public void add(E element) { root = add(root, element); } /** * 向根节点为 node 的二分搜索树中添加元素 element * 递归函数 * @param node 添加元素的二分搜索树的根节点 * @param element 添加的元素 * @return 返回插入新节点后的二分搜索树的根节点 */ private Node add(Node node, E element) { // 终止条件 if (node == null) { // 递归到空节点时,new 一个根节点将元素添加到该节点中并返回该节点给上一层的二分搜索树的左节点或右节点或者 root 根节点接收 size++; return new Node(element); } // 不满足终止条件时,递归的进行添加元素 if (element.compareTo(node.element) < 0) { // 比当前节点小,添加到左子树中,并使用当前节点的左节点接收结果 node.left = add(node.left, element); } else if (element.compareTo(node.element) > 0) { // 比当前节点大,添加到右子树中,并使用当前节点的右节点接收结果 node.right = add(node.right, element); } // 最后返回起始时的 node 节点给上层左节点或右节点或者 root 根节点接收 return node; }
查询操作
-
对于二分搜索树的查询操作,这里实现一个 contains 方法用于判断要查找的元素是否存在于二分搜索树中,如果存在返回 true,如果不存在返回 false。
-
对于这个操作的实现步骤如下(递归实现):
- 首先判断当前递归到的根节点是否为空,如果为空则说明当前递归到的树没有元素,返回 false。
- 接着判断当前递归到的根节点中的元素是否为要查找的元素,如果是则返回 true,否则进行后续的判断。
- 对于剩下的判断则是判断要查找的元素是大于还是小于当前递归到的根节点,大于就在右子树中继续寻找,小于则在左子树中继续寻找,接着继续以上 1、2、3 步的操作,直至出现结果为止。
-
此操作实现代码为下:
/** * 查看二分搜索树中是否包含元素 element * @param element 查找的元素 * @return 包含元素 element 返回 true;反之返回 false */ public boolean contains(E element) { // 在整棵树中查找 return contains(root, element); } /** * 查看以 node 为根的二分搜索树中是否包含元素 element * 递归函数 * @param node 进行查找的二分搜索树的根节点 * @param element 查找的元素 * @return 包含元素 element 返回 true;反之返回 false */ private boolean contains(Node node, E element) { if (node == null) { // 当前查找的二分搜索树的根节点为空的话,返回 false return false; } if (element.compareTo(node.element) == 0) { // 当前递归到的根节点的元素为 element,包含,返回 true return true; } else if (element.compareTo(node.element) < 0) { // 如果 element 比当前根节点的元素小,在左子树中寻找 return contains(node.left, element); } else { // 如果 element 比当前根节点的元素大,在右子树中寻找 return contains(node.right, element); } }
遍历操作
- 对于遍历,这个操作是十分常见的。在二分搜索树中,遍历操作就是把所有的节点都访问一遍。在前面的线性结构中,遍历是及其容易的,使用循环就行了。不过在树结构中遍历也比线性结构难不了多少,也是比较简单的。在树结构中有这么几种遍历:前序遍历、中序遍历、后序遍历、层序遍历,下面就一一简单地实现出二分搜索树中的这几种遍历方式。
前序遍历
-
对于二分搜索树的前序遍历操作,同样也是使用递归来实现。对于前序遍历,遍历的顺序是先访问当前节点,接着访问该节点的左子树继而访问该节点的右子树,在子树中也是重复此步骤。当遍历到一个节点为 null 时直接返回即可。用图来表示这个过程就是以下所示:
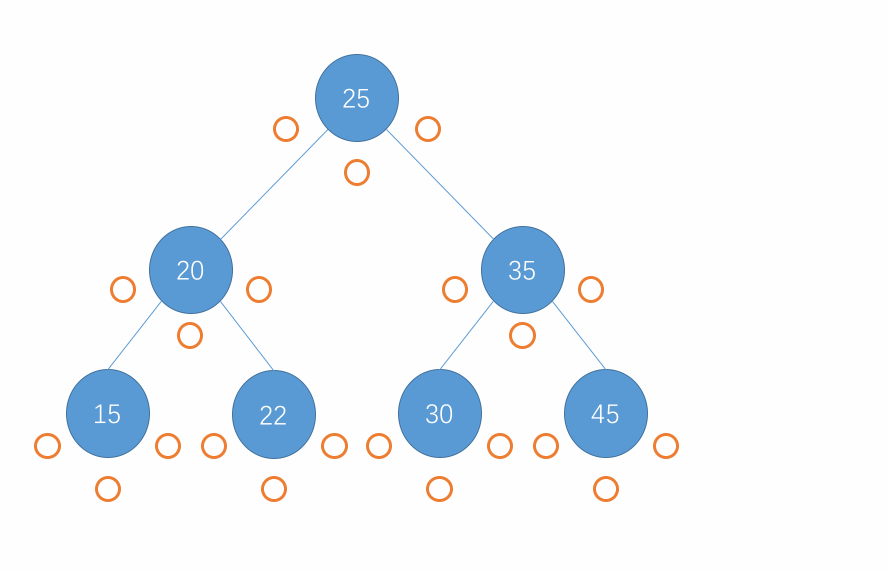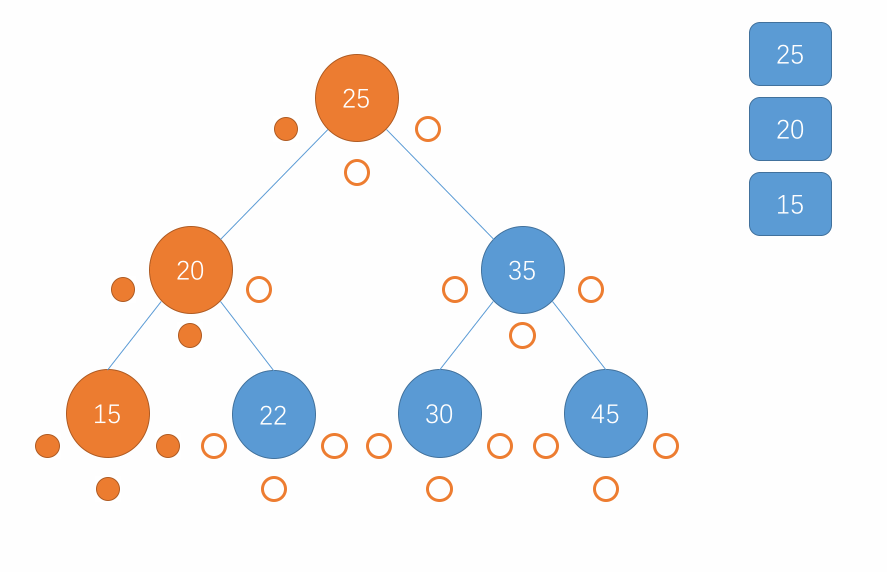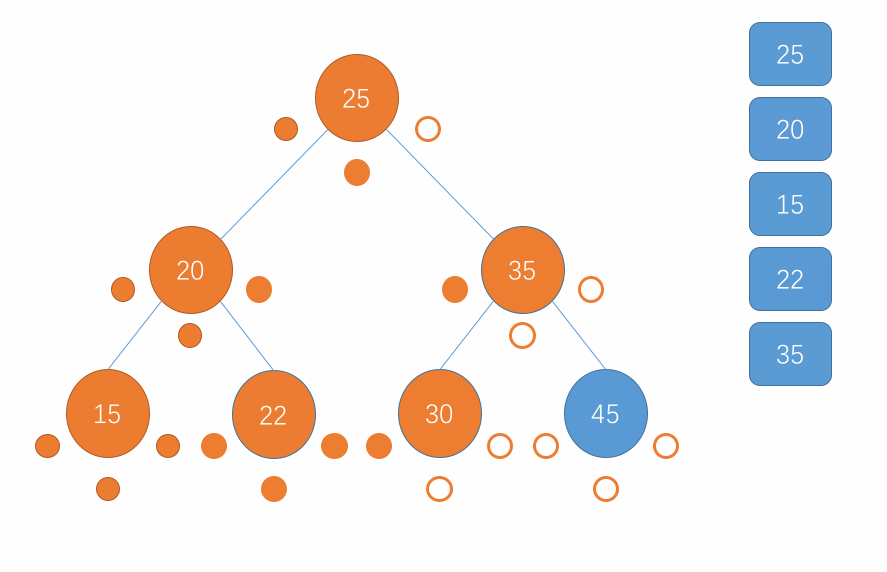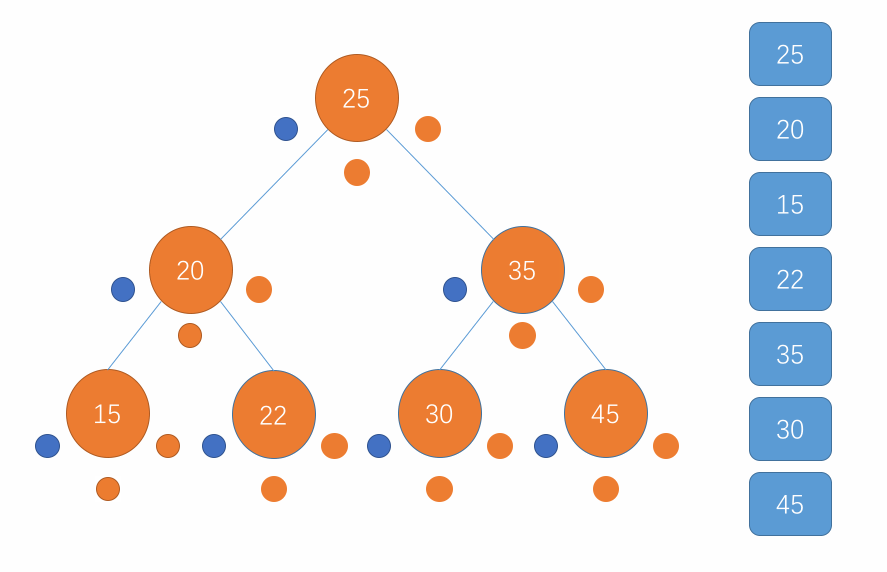
-
以上过程实现为代码形式如下:
/** * 二分搜索树的前序遍历 */ public void preOrder() { // 从根节点开始遍历 preOrder(root); } /** * 前序遍历以 node 为根的二分搜索树 * 递归函数 * @param node 前序遍历的二分搜索树的根节点 */ private void preOrder(Node node) { // 终止条件 if (node == null) { // 遍历到空节点时直接返回即可 return; } // 访问节点操作(此处简单的打印一下节点中存储的元素) System.out.println("element: " + node.element); // 遍历当前节点的左子树 preOrder(node.left); // 遍历当前节点的右子树 preOrder(node.right); } -
实现了代码之后,做个小测试验证一下是否正确,测试代码如下:
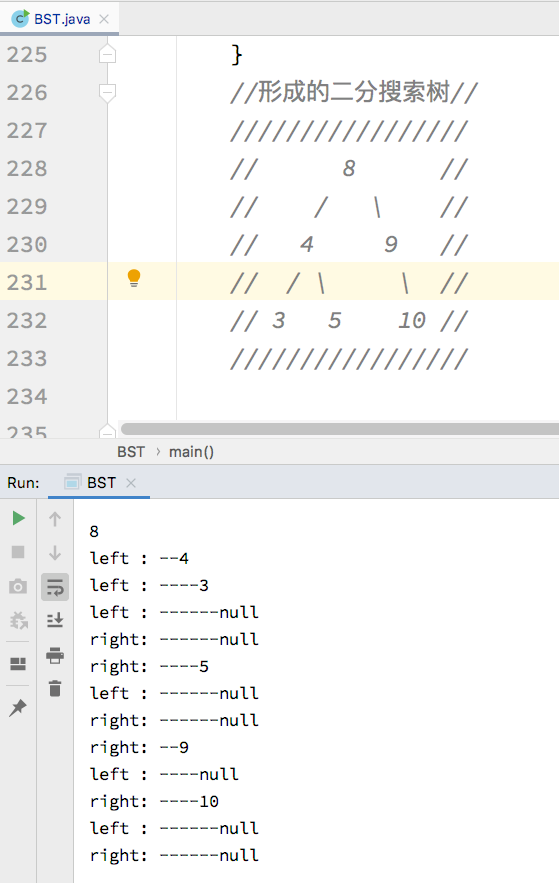
/** * 测试 BST */ public static void main(String[] args) { BST<Integer> bst = new BST<>(); int[] nums = {8, 4, 9, 10, 5, 3}; for (int num : nums) { bst.add(num); } //形成的二分搜索树// ///////////////// // 8 // // / / // // 4 9 // // / / / // // 3 5 10 // ///////////////// // 前序遍历 bst.preOrder(); } -
测试结果如下,可以看出结果是符合前序遍历的规则的,验证了代码的正确性:
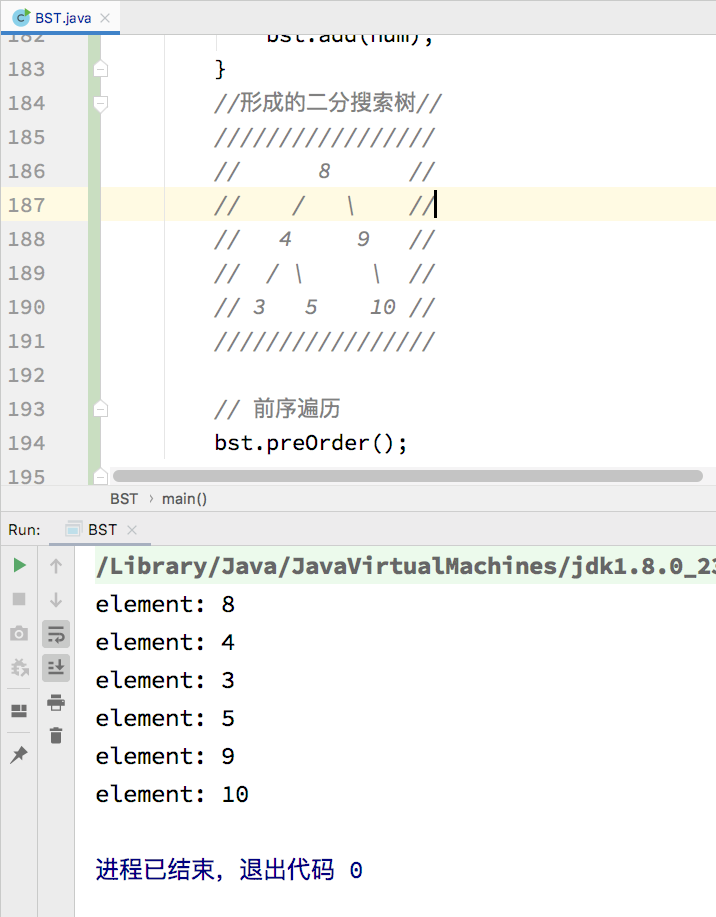
-
在实现了前序遍历之后,可以使用前序遍历的方式为这个 BST 类重写一下 toString 方法打印出二分搜索树以便观察。
-
实现代码如下:
/** * 重写 toString 方法打印二分搜索树 */ @Override public String toString() { StringBuilder result = new StringBuilder(); generateBSTString(root, 0, result); return result.toString(); } /** * 生成以 node 为根节点,深度从 depth 开始的二分搜索树的字符串 * @param node 根节点 * @param depth 深度 * @param result 生成的结果 */ private void generateBSTString(Node node, int depth, StringBuilder result) { if (node == null) { result.append(generateDepthString(depth) + "null/n"); return; } result.append(generateDepthString(depth) + node.element + "/n"); result.append("left : "); generateBSTString(node.left, depth + 1, result); result.append("right: "); generateBSTString(node.right, depth + 1, result); } /** * 根据当前深度打印出当前深度对应的 -- 数量 * @param depth 当前深度 * @return 返回当前深度对应数量的 -- 字符串 */ private String generateDepthString(int depth) { StringBuilder result = new StringBuilder(); for (int i = 0; i < depth; i++) { result.append("--"); } return result.toString(); } -
同样也对此测试一下:
/** * 测试 BST */ public static void main(String[] args) { BST<Integer> bst = new BST<>(); int[] nums = {8, 4, 9, 10, 5, 3}; for (int num : nums) { bst.add(num); } //形成的二分搜索树// ///////////////// // 8 // // / / // // 4 9 // // / / / // // 3 5 10 // ///////////////// // 前序遍历 bst.preOrder(); System.out.println("/n==========/n"); System.out.println(bst); } -
运行效果如下,可以看出同一层的节点都打印了正确的深度,遍历的顺序也满足了前序遍历的规则:
-
至此,就完成了前序遍历的实现,对于下面的中序遍历和后序遍历本质上实现方式和前序遍历差不了多少,只是节点的访问顺序变化了。
中序遍历
-
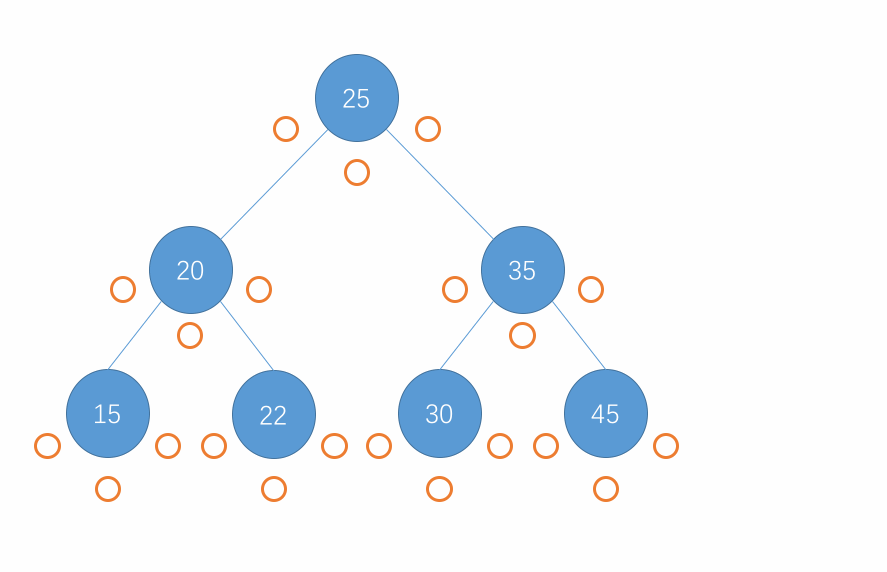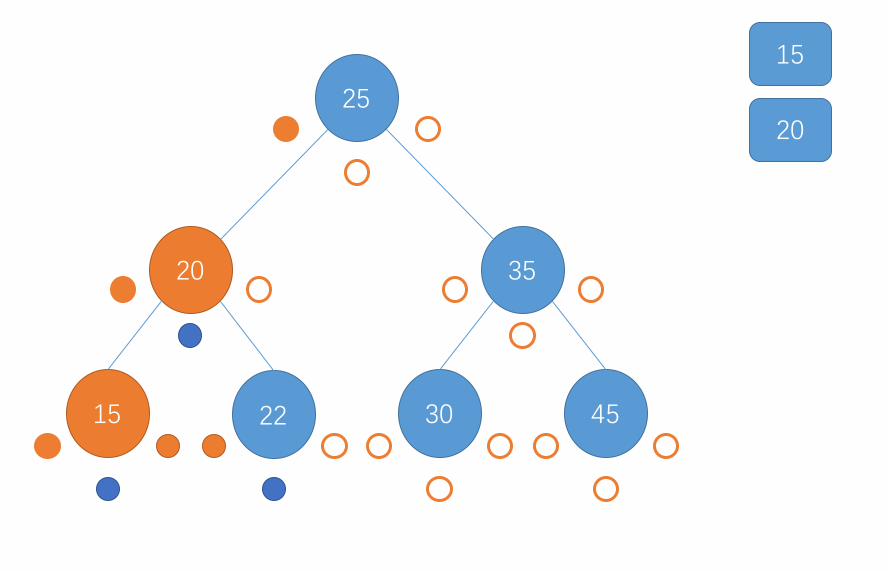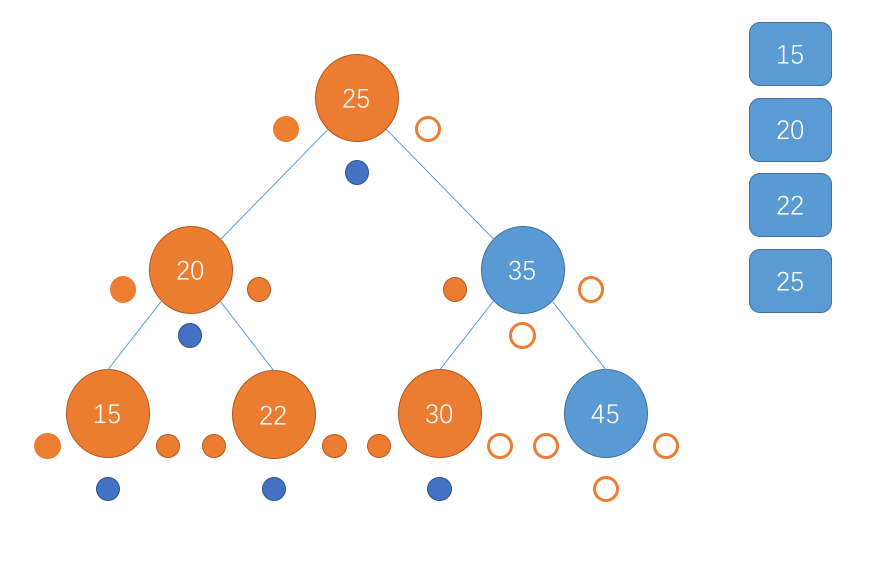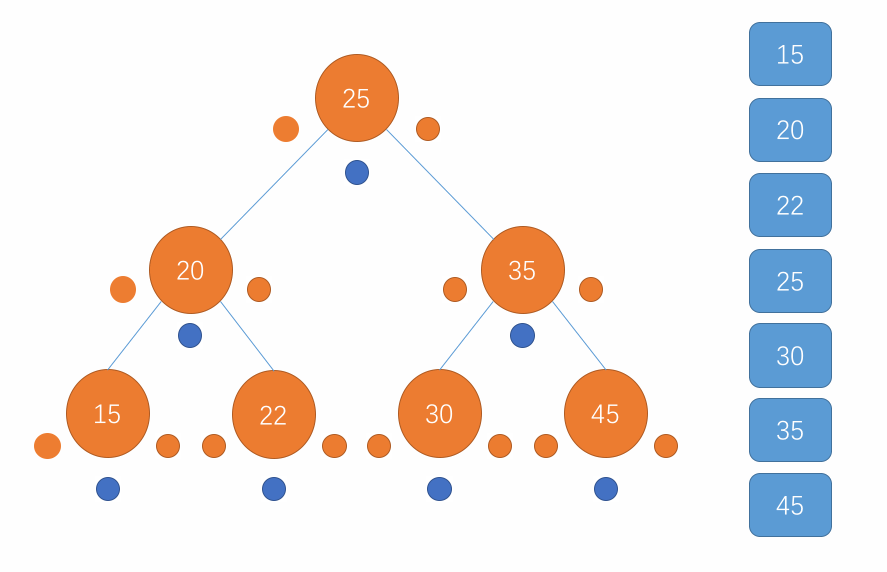
对于中序遍历,遍历的顺序是先访问当前节点的左子树,接着访问该节点继而访问该节点的右子树,在子树中也是重复此步骤。当遍历到一个节点为 null 时直接返回即可。用图来表示这个过程就是以下所示:
-
以上过程实现为代码形式如下:
/** * 二分搜索树的中序遍历 */ public void inOrder() { inOrder(root); } /** * 中序遍历以 node 为根的二分搜索树 * 递归函数 * @param node 中序遍历的二分搜索树的根节点 */ private void inOrder(Node node) { // 终止条件 if (node == null) { // 遍历到空节点时直接返回即可 return; } // 遍历当前节点的左子树 inOrder(node.left); // 访问节点操作(此处简单的打印一下节点中存储的元素) System.out.println("element: " + node.element); // 遍历当前节点的右子树 inOrder(node.right); } -
同样对此也调用该方法测试一下,运行结果如下,可以看出输出的顺序符合中序遍历的规则,验证了代码的正确性:
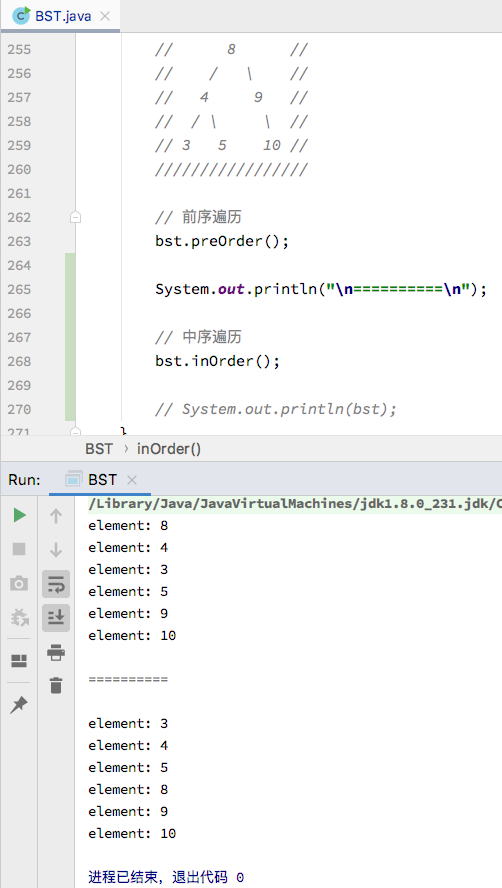
-
从结果中也可以看出中序遍历的一个特点:输出的结果是排好序后的。原因在于二分搜索树的左子树是小于父亲节点,右子树大于父亲节点,而中序遍历的顺序正好是先访问左子树,接着访问父亲节点,最后再访问右子树。所以输出的结果是按从小到大的顺序输出的。
后序遍历
-
对于后序遍历,遍历的顺序是先访问当前节点的左子树,接着访问该节点的右子树继而访问该节点,在子树中也是重复此步骤。当遍历到一个节点为 null 时直接返回即可。用图来表示这个过程就是以下所示:
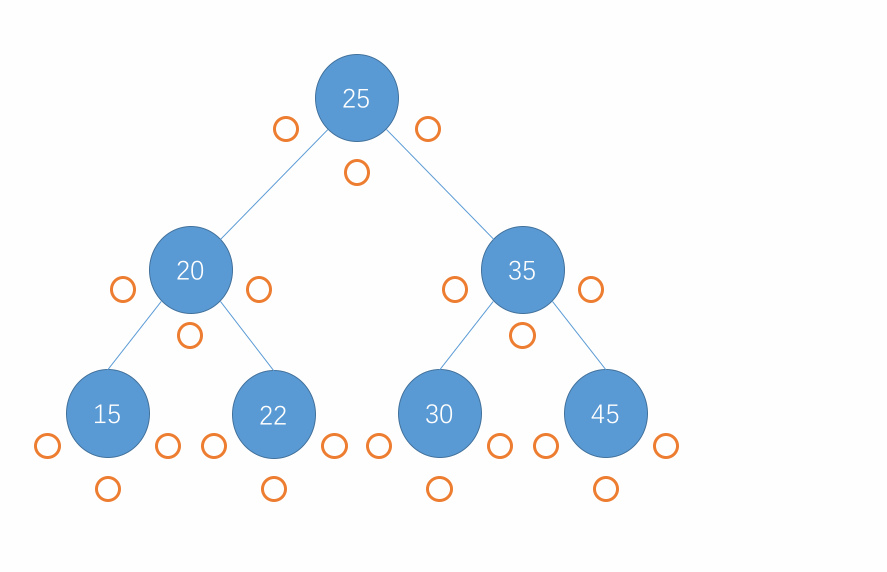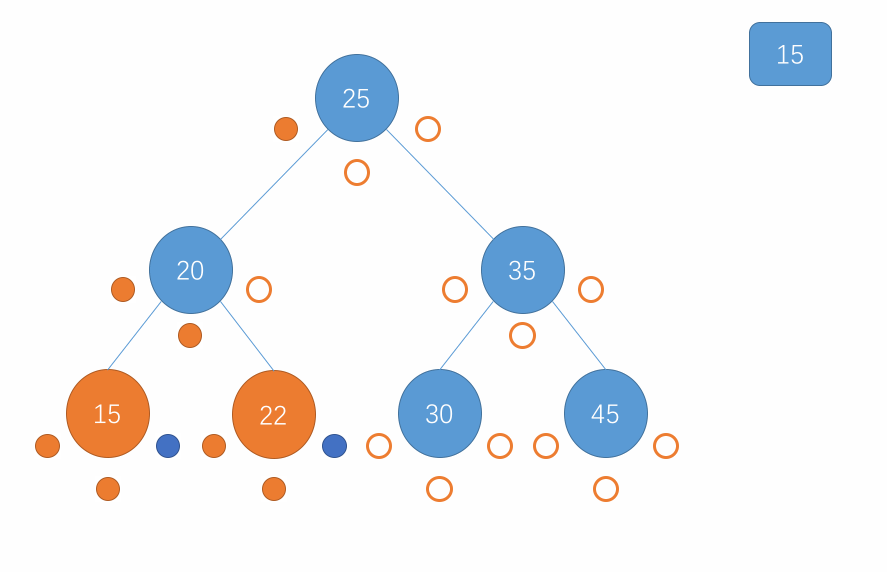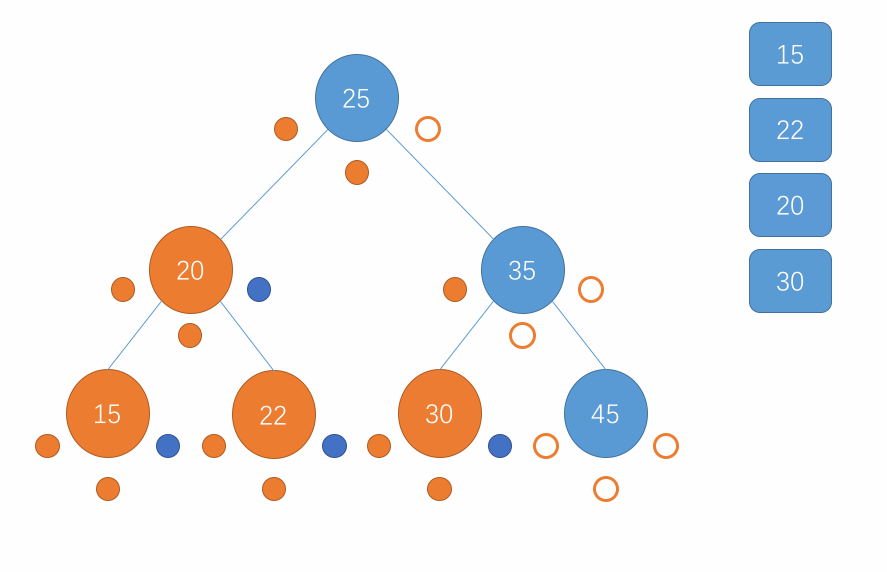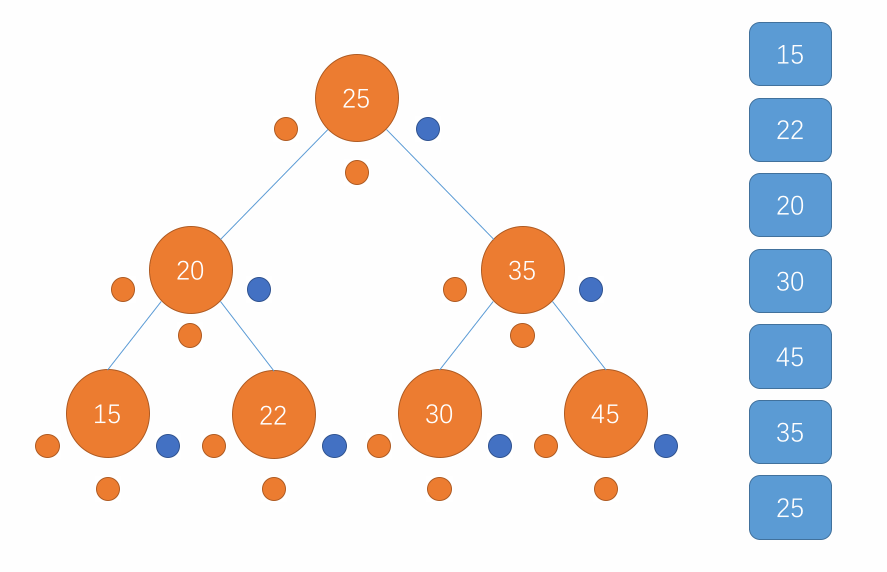
-
以上过程实现为代码形式如下:
/** * 二分搜索树的后序遍历 */ public void postOrder() { postOrder(root); } /** * 后序遍历以 node 为根的二分搜索树 * 递归函数 * @param node 后序遍历的二分搜索树的根节点 */ private void postOrder(Node node) { // 终止条件 if (node == null) { // 遍历到空节点时直接返回即可 return; } // 遍历当前节点的左子树 postOrder(node.left); // 遍历当前节点的右子树 postOrder(node.right); // 访问节点操作(此处简单的打印一下节点中存储的元素) System.out.println("element: " + node.element); } -
同样对此也调用该方法测试一下,运行结果如下,可以看出输出的顺序符合中序遍历的规则,验证了代码的正确性:
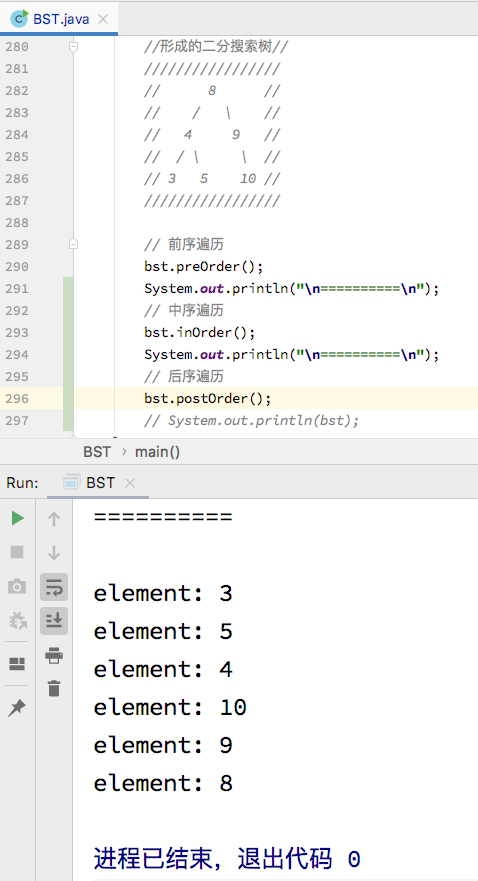
-
从结果中也可以看出后序遍历是按从后往前的顺序由子节点开始一一遍历到父节点的,这种特性也应对了一种应用:为二分搜索树释放内存。当想要为一个符合二分搜索树特性的模型释放内存的时候,就可以使用二分搜索树的后序遍历来完成。
前、中、后序遍历的非递归实现
- 在实现了前、中、后序遍历的递归方式之后,可以使用非递归方式对这三种遍历一一再实现一次,加深对二分搜索树的理解。
- 在对递归的学习中,可以知道递归调用函数的时候是会被压入到系统栈中记录执行顺序的,当执行完之后就进行出栈回到上一次调用函数的地方继续执行余下操作。
- 所以对于非递归的实现,可以借助栈这个数据结构,手动模拟系统栈的方式实现二分搜索树的前、中、后序遍历。接下来一一实现这三种遍历的非递归方式。
前序遍历的非递归实现
-
对于使用栈来帮助模拟系统栈来实现前序遍历的过程,用动图来表示如下所示:
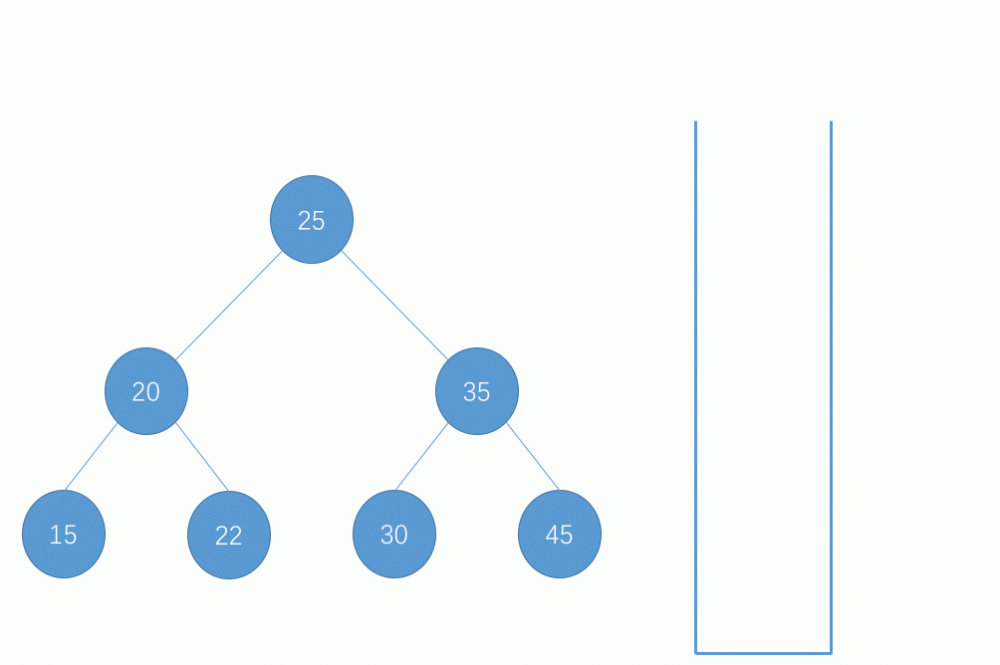
-
对于以上过程,由于栈的后进先出的特性,加上前序遍历的规则,所以在遍历完一个节点将其出栈后是先将该节点的右节点先入栈再入栈左节点,这样子后续出栈遍历节点后就满足了前序遍历的规则。
-
以上过程代码实现如下:
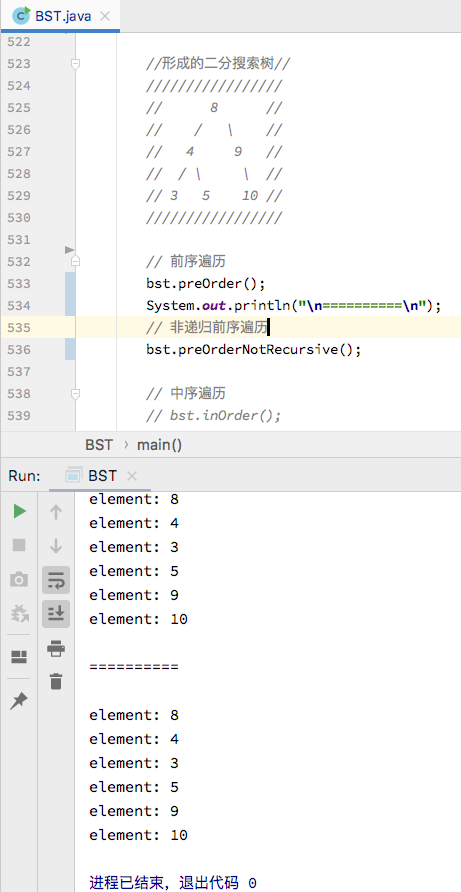
/** * 二分搜索树的非递归方式的前序遍历 */ public void preOrderNotRecursive() { // 如果树为空,则不遍历,没有元素可遍历 if (root == null) { return; } // 借助一个栈来模拟系统栈实现前序遍历 Stack<Node> stack = new Stack<>(); // 从根节点开始遍历 stack.push(root); // 当栈非空时,循环往复以下过程对二分搜索树进行前序遍历 while (!stack.isEmpty()) { // 当前遍历的节点 Node currentNode = stack.pop(); System.out.println("element: " + currentNode.element); // 如果当前遍历的节点的左右节点不为空,按右节点、左节点的顺序入栈 if (currentNode.right != null) { stack.push(currentNode.right); } if (currentNode.left != null) { stack.push(currentNode.left); } } } -
实现之后,调用之前的递归方式和这个非递归方式比对两者的结果是否一致:
-
从结果可看出,非递归方式的实现是正确的。对比递归实现的步骤,非递归的实现相对来说还是比较复杂的,不过通过这样的实现也能加强对于二分搜索树前序遍历的理解,还是相当有好处的,接着继续实现中序遍历和后序遍历的非递归方式的实现。
中序遍历的非递归实现
-
对于中序遍历的非递归实现,同样也是使用一个栈来模拟系统栈的递归过程来实现,首先在这里先使用一个内部类用于封装当前的指令(继续模拟递归、打印节点)和当前模拟递归到的节点,以便模拟栈递归实现中序遍历。
-
对于这个内部类的具体实现如下所示,其中 s 代表指令,如果 s 为 go 则表示继续模拟递归,如果 s 为 print 则表示打印当前节点信息。
/** * 用于封装模拟系统栈时的指令和递归到的节点信息 */ private class Command { // s: 指令 // go: 表示继续模拟递归 // print: 表示打印当前节点信息 private String s; // 当前模拟递归到的节点 private Node node; public Command(String s, Node node){ this.s = s; this.node = node; } } -
当封装了这么一个内部类之后,非递归方式的中序遍历就比较好实现了,具体过程为:
- 初始时将根节点和指令 go 入栈,表示从根节点开始继续模拟递归下去。
- 接着开始循环,只要栈不为空,就重复循环中的内容:
- 首先先从栈顶取出当前栈顶信息。
- 接着判断栈顶信息中的指令是否为 print,如果为 print 打印节点信息,否则做下面的操作。
- 如果指令为 go,则将当前节点的右子树和指令 go 先入栈。(和前面的非递归前序遍历一样,由于栈的后入先出特性,需要反过来入栈,后面出栈时才能符合中序遍历)
- 接着将当前节点和指令 print 入栈,当后面这个节点出栈时就可以判断到 print 指令打印这个节点。
- 最后再将当前节点的左子树和指令 go 入栈,这样子后面最先出栈的就是左节点再到左节点的父节点再到右节点,满足中序遍历的规则。
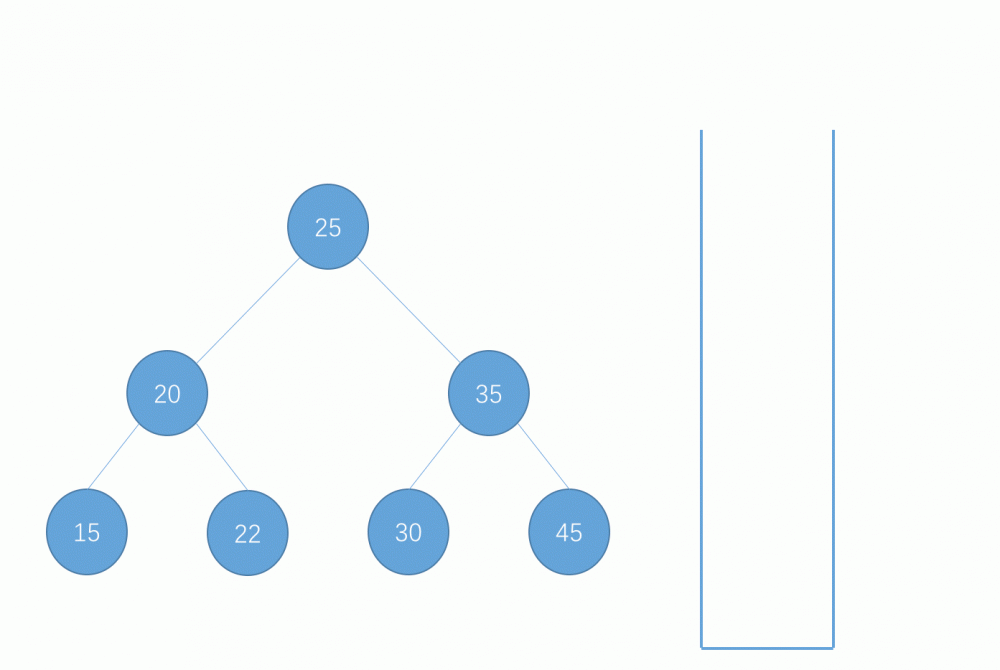
- 这样子,重复以上过程,就可以模拟系统栈的递归实现出二分搜索树的中序遍历了,以上过程的图示演示如下:
-
具体代码实现如下:
/** * 二分搜索树的非递归方式的中序遍历 */ public void inOrderNotRecursive() { // 如果树为空,则不遍历,没有元素可遍历 if (root == null) { return; } // 借助一个栈来模拟系统栈实现中序遍历 Stack<Command> stack = new Stack<>(); // 初始时将根节点和指令 go 入栈 stack.push(new Command("go", root)); // 当栈非空时,循环往复以下过程对二分搜索树进行中序遍历 while (!stack.isEmpty()) { // 将栈顶信息出栈,判断其中的指令做相应操作 Command command = stack.pop(); if ("print".equals(command.s)) { System.out.println("element: " + command.node.element); } else { if (command.node.right != null) { stack.push(new Command("go", command.node.right)); } stack.push(new Command("print", command.node)); if (command.node.left != null) { stack.push(new Command("go", command.node.left)); } } } } -
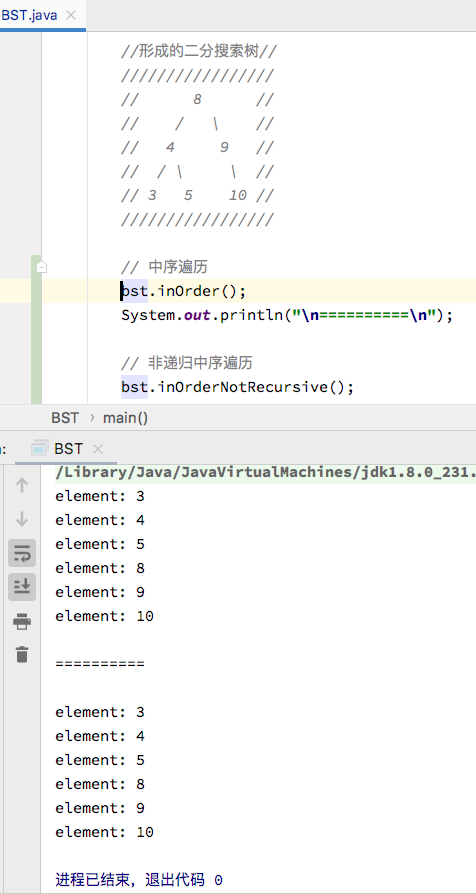
同样地,也对此进行测试,验证是否编写正确,运行结果如下:
-
从测试结果可以看出,遍历的结果是符合预期的,和之前实现的递归方式的结果是一致的,验证了代码的正确性。在实现完了非递归方式的中序遍历后,对于后序遍历也就手到擒来了,原理也是相似的,接下来就实现后序遍历的非递归方式。
后序遍历的非递归实现
-
对于后序遍历的非递归方式的实现,同样也是使用 Command 来封装入栈的信息。其中的具体实现过程如下:
- 初始时将根节点和指令 go 入栈,表示从根节点开始继续模拟递归下去。
- 接着开始循环,只要栈不为空,就重复循环中的内容:
- 首先先从栈顶取出当前栈顶信息。
- 接着判断栈顶信息中的指令是否为 print,如果为 print 打印节点信息,否则做下面的操作。
- 如果指令为 go,则将当前节点和指令 print 先入栈,当后面这个节点出栈时就可以判断到 print 指令打印这个节点。(和前面的非递归前序遍历一样,由于栈的后入先出特性,需要反过来入栈,后面出栈时才能符合后序遍历)
- 接着将当前节点的右子树和指令 go 入栈。
- 最后再将当前节点的左子树和指令 go 入栈,这样子后面最先出栈的就是左节点再到右节点再到左右节点的父节点,满足后序遍历的规则。
- 这样子,重复以上过程,就可以模拟系统栈的递归实现出二分搜索树的后序遍历了,以上过程的图示演示如下:

-
具体代码实现如下:
/** * 二分搜索树的非递归方式的后序遍历 */ public void postOrderNotRecursive() { // 如果树为空,则不遍历,没有元素可遍历 if (root == null) { return; } // 借助一个栈来模拟系统栈实现后序遍历 Stack<Command> stack = new Stack<>(); // 初始时将根节点和指令 go 入栈 stack.push(new Command("go", root)); // 当栈非空时,循环往复以下过程对二分搜索树进行后序遍历 while (!stack.isEmpty()) { // 将栈顶信息出栈,判断其中的指令做相应操作 Command command = stack.pop(); if ("print".equals(command.s)) { System.out.println("element: " + command.node.element); } else { stack.push(new Command("print", command.node)); if (command.node.right != null) { stack.push(new Command("go", command.node.right)); } if (command.node.left != null) { stack.push(new Command("go", command.node.left)); } } } } -
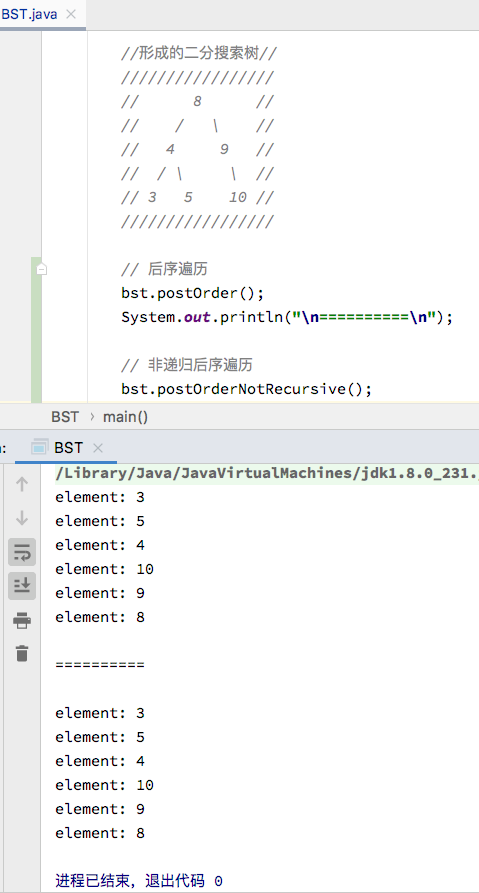
同样地,也对此进行测试,验证是否编写正确,运行结果如下:
-
从测试结果可以看出,遍历的结果是符合预期的,和之前实现的递归方式的结果是一致的,验证了代码的正确性。至此,就将前、中、后序遍历的非递归方式都实现了一遍了,使用的是模拟系统栈的方式,如此也加深了对这三种遍历的理解以及对递归的理解,接下来就实现二分搜索树中的最后一种遍历层序遍历。
层序遍历
-
在前面的前、中、后序三种遍历方式的实现过程中,可以发现这三种遍历方式总是会先到最下层的节点处再往上返回,这种方式也就是深度优先遍历。
-
而对于层序遍历而言,它是按一层一层从左往右的顺序来遍历的,这种方式也就是广度优先遍历。
-
对于这种遍历方式,通常使用的实现方式是非递归方式的实现,同时可以借助队列这个数据结构来实现。
-
对于实现过程,当一个节点入队并出队时,这个节点就被遍历到了,同时在该节点出队时,由于队列的先入先出特性以及层序遍历的规则,此时将该节点的左右节点按左节点、右节点的顺序入队,此时再当队首的节点出队时,又再将出队节点的左右节点按左节点、右节点的顺序入队。以此类推循环往复,就完成了二分搜索树的层序遍历操作,这个过程用图来表示如下所示:
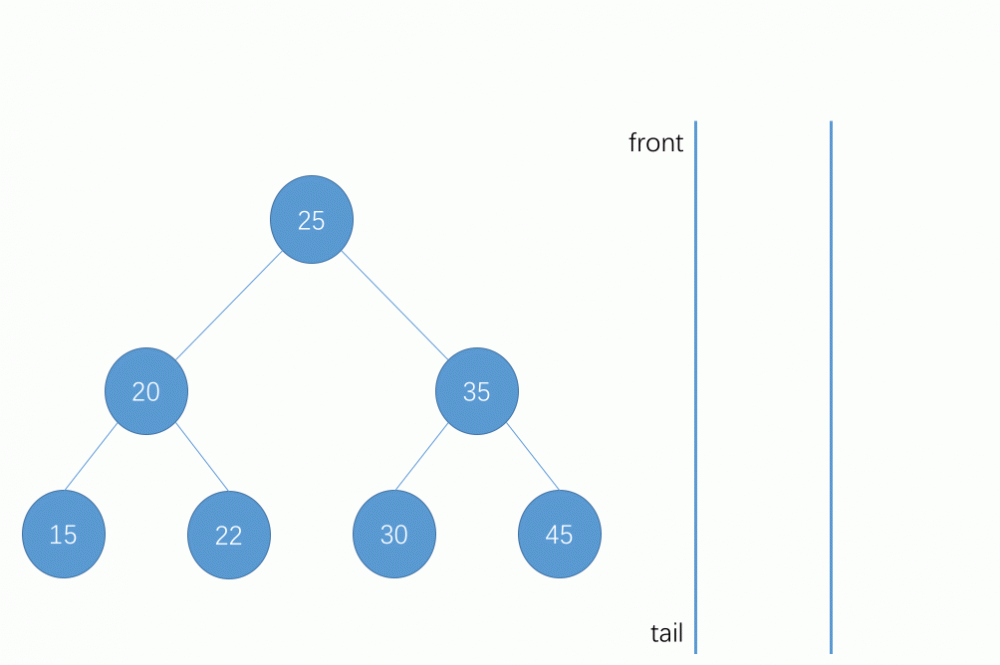
-
以上过程代码实现如下:
/** * 二分搜索树的层序遍历 */ public void levelOrder() { // 借助一个队列来实现层序遍历 Queue<Node> queue = new LinkedList<>(); // 从根节点开始遍历 queue.add(root); // 当队列非空时,循环往复以下过程对二分搜索树进行层序遍历 while (!queue.isEmpty()) { // 当前遍历的节点 Node currentNode = queue.remove(); System.out.println(currentNode.element); // 如果当前遍历的节点的左右节点不为空,按左节点、右节点的顺序入队 if (currentNode.left != null) { queue.add(currentNode.left); } if (currentNode.right != null) { queue.add(currentNode.right); } } } -
此时调用该方法验证是否正确:
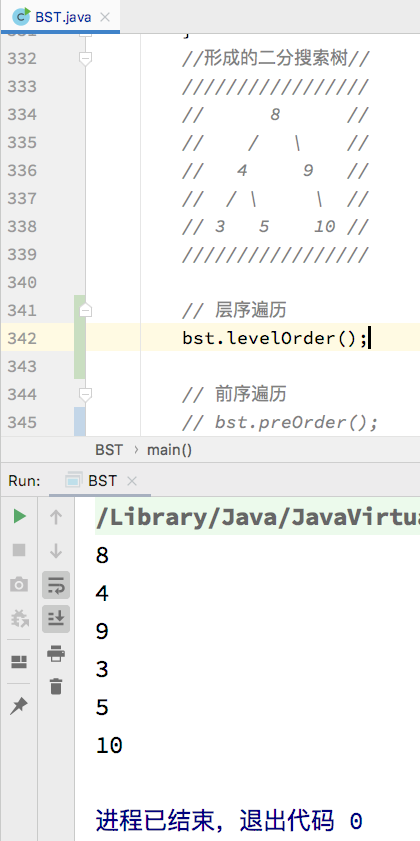
-
从结果可看出,遍历的顺序符合了预期,验证了代码的正确性。至此,二分搜索树的几种遍历方式也就都实现了,接下来实现最后的删除操作。
删除操作
删除最大元素和最小元素
-
对于删除操作,首先先从删除二分搜索树的最大值和最小值开始,因为根据二分搜索树的特性,最左边的节点就是整棵树的最小值,最右边的节点就是整棵树的最大值,所以相对来说这两个操作比较容易实现,同时先实现了这两个操作后,对于后续的删除任意元素也有辅助的作用。以下是最大值和最小值的几个示例图:

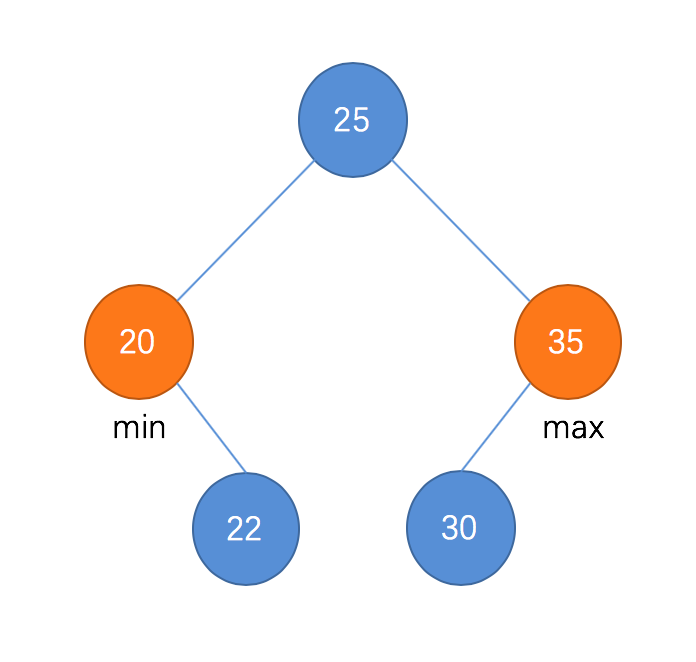
-
在实现删除的操作之前,先实现两个函数用于找到二分搜索树的最小元素和最大元素以备删除时使用,具体实现如下:
/** * 找到二分搜索树的最小元素 * @return 返回当前二分搜索树的最小元素 */ public E minimum() { // 判断当前二分搜索树是否为空树 if (size == 0) { throw new IllegalArgumentException("Minimum failed. Current BST is empty!"); } return minimum(root).element; } /** * 返回以 node 为根的二分搜索树的最小值所在的节点 * @param node 寻找最小值的二分搜索树的根节点 * @return 返回当前二分搜索树的最小元素 */ private Node minimum(Node node) { // 当一个节点的左节点为空时,该节点就是树中的最左节点了 if (node.left == null) { return node; } // 否则继续往左子树中寻找 return minimum(node.left); } /** * 找到二分搜索树的最大元素 * @return 返回当前二分搜索树的最大元素 */ public E maximum() { // 判断当前二分搜索树是否为空树 if (size == 0) { throw new IllegalArgumentException("Maximum failed. Current BST is empty!"); } return maximum(root).element; } /** * 返回以 node 为根的二分搜索树的最大值所在的节点 * @param node 寻找最大值的二分搜索树的根节点 * @return 返回当前二分搜索树的最大元素 */ private Node maximum(Node node) { // 当一个节点的右节点为空时,该节点就是树中的最右节点了 if (node.right == null) { return node; } // 否则继续往右子树中寻找 return maximum(node.right); } -
在实现完以上函数之后,就可以进行删除的操作了。
-
首先先进行最小值的删除,对于最小值的删除,有两种情况:删除的节点是叶子节点、删除的节点有右子树。
-
对于叶子节点,直接删除即可。而对于有右子树的节点,删除的逻辑也很简单,即将当前的节点和树脱离,再将这个节点的右子树接到它原来的位置即可。而对于叶子节点,它的左右节点都是 null 的,所以对于叶子节点也可以使用这个逻辑来删除,只不过接到节点原来位置的是 null 而已。
-
以上过程的图示如下:
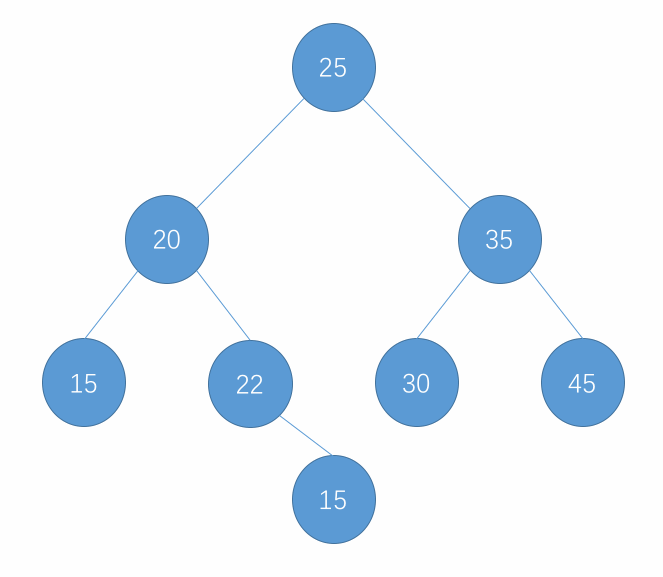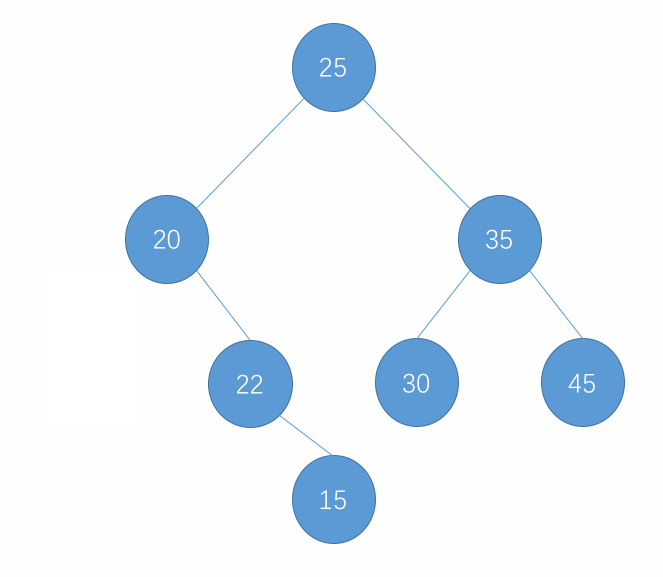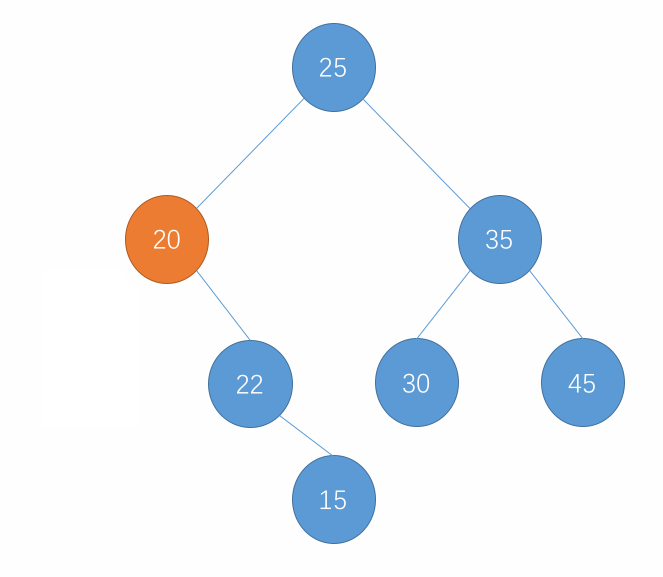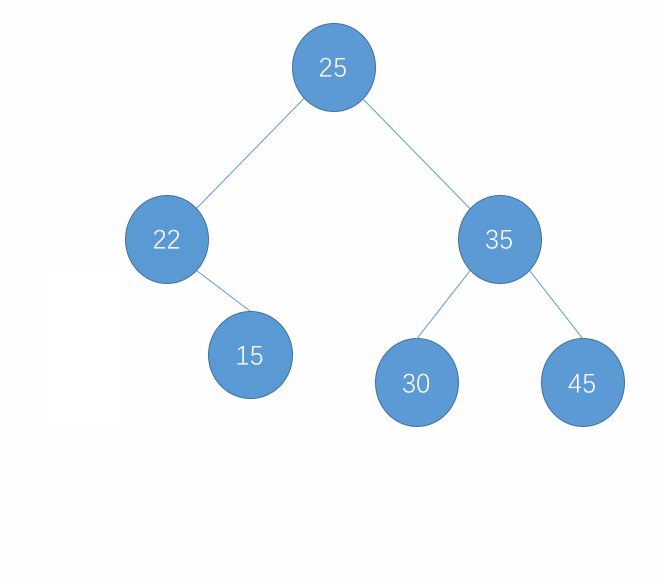
-
代码实现如下:
/** * 删除二分搜索树中最小值所在的节点并且返回删除的最小值 * @return 返回删除的节点中的元素 */ public E removeMin() { // 先接收当前二分搜索树中的最小值,以备删除后返回 E delElement = minimum(); // 删除操作 root = removeMin(root); // 返回删除的最小值 return delElement; } /** * 删除以 node 为根的二分搜索树的最小节点 * @param node 删除最小节点的二分搜索树的根节点 * @return 返回删除节点后新的二分搜索树的根,即删除的节点的右子树的根节点 */ private Node removeMin(Node node) { // 当递归到一个节点的左节点为空时,此节点为最小节点,进行删除操作 if (node.left == null) { // 先将删除的节点 node 的右子树记录下来 Node rightNode = node.right; // 将 node 和它的右子树脱离 node.right = null; size--; // 返回 node 的右子树给上层节点接收,此时 node 和上层节点也脱离了 return rightNode; } // 左节点不为空时,继续往左子树递归,使用当前根节点的左节点接收 node.left = removeMin(node.left); // 最后返回当前根节点,完成删除 return node; } -
在处理完了最小元素的删除之后,对于最大的元素删除就容易许多了,删除的逻辑总体上还是一样的,也就是把删除节点的左子树接到节点原来的位置即可。删除过程图示如下:
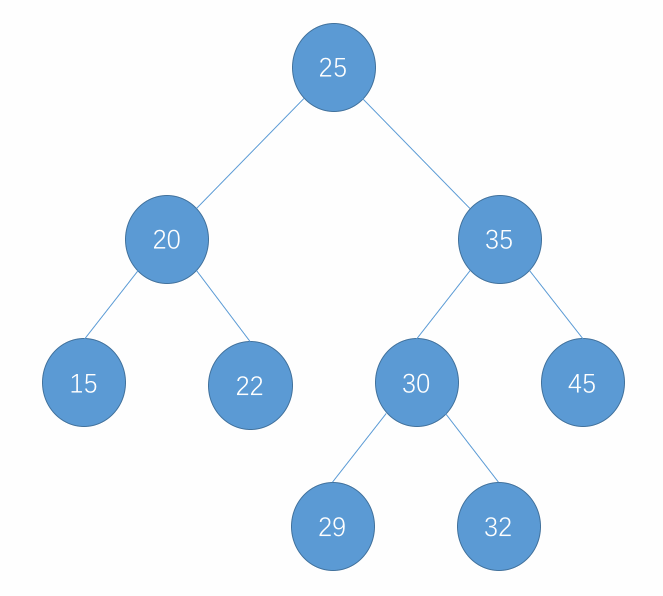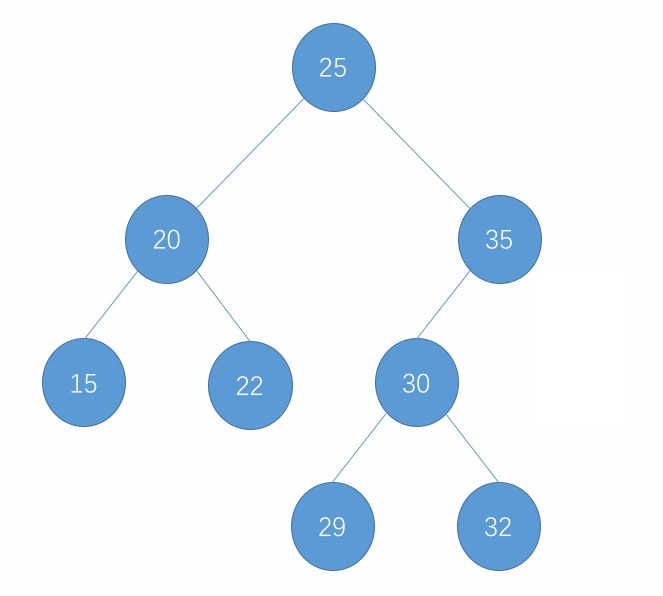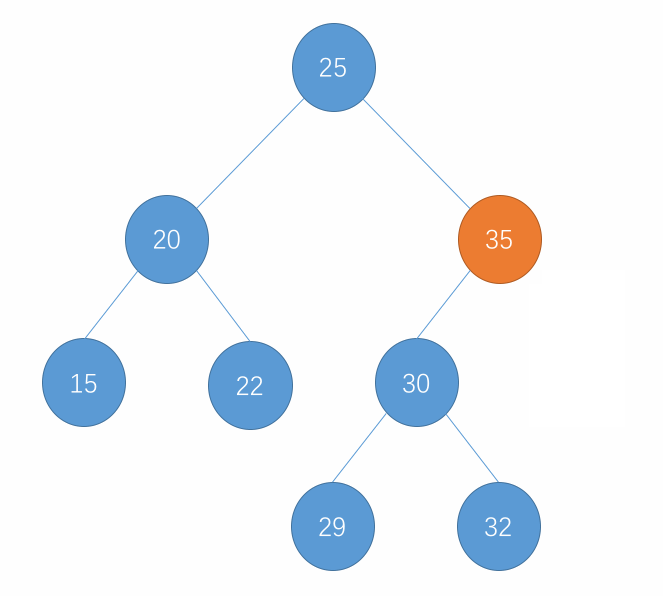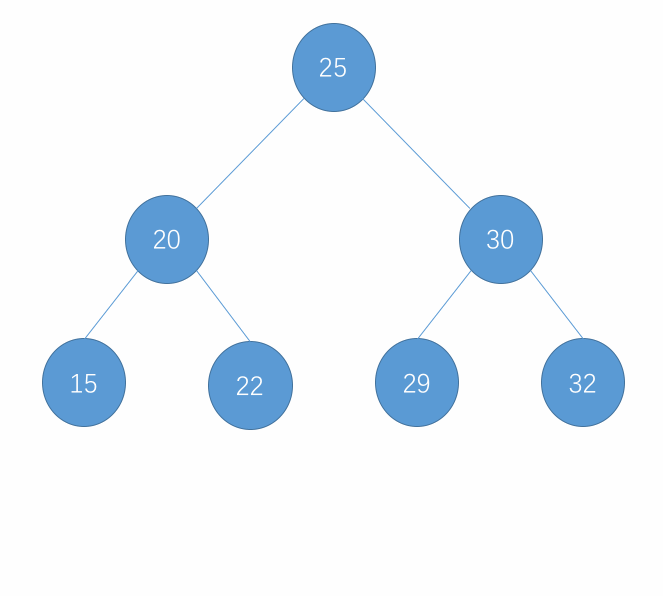
-
代码实现如下:
/** * 删除二分搜索树中最大值所在的节点并且返回删除的最大值 * @return 返回删除的节点中的元素 */ public E removeMax() { // 先接收当前二分搜索树中的最大值,以备删除后返回 E delElement = maximum(); // 删除操作 root = removeMax(root); // 返回删除的最小值 return delElement; } /** * 删除以 node 为根的二分搜索树的最大节点 * @param node 删除最大节点的二分搜索树的根节点 * @return 返回删除节点后新的二分搜索树的根,即删除的节点的左子树的根节点 */ private Node removeMax(Node node) { // 当递归到一个节点的右节点为空时,此节点为最大节点,进行删除操作 if (node.right == null) { // 先将删除的节点 node 的左子树记录下来 Node leftNode = node.left; // 将 node 和它的左子树脱离 node.left = null; size--; // 返回 node 的左子树给上层节点接收,此时 node 和上层节点也脱离了 return leftNode; } // 右节点不为空时,继续往右子树递归,使用当前根节点的右节点接收 node.right = removeMax(node.right); // 最后返回当前根节点,完成删除 return node; } -
在实现了以上两个操作之后,对它们进行一下测试。
-
测试的逻辑为:随机生成 1000 个 [0, 10000) 的数添加到二分搜索树中,然后分别使用这两个操作将删除的元素添加到一个 ArrayList 中,再对这个 ArrayList 进行校验,看看里面的元素是不是按从小到大的顺序或从大到小的顺序排列,校验成功的话说明以上的操作实现的代码是正确的。
-
测试代码如下所示:
private static void testRemoveMin() { // 测试删除最小节点 BST<Integer> bst = new BST<>(); Random random = new Random(); int n = 1000; for (int i = 0; i < n; i++) { bst.add(random.nextInt(10000)); } ArrayList<Integer> nums = new ArrayList<>(); while (!bst.isEmpty()) { nums.add(bst.removeMin()); } // 校验 nums 是否按从小到大的顺序排列 for (int i = 1; i < nums.size(); i++) { if (nums.get(i - 1) > nums.get(i)) { // 如果有一个数比后面的大,则说明删除最小节点的操作的实现是错误的 throw new IllegalArgumentException("removeMin error!"); } } // 运行到此处校验通过 System.out.println("removeMin test completed."); } private static void testRemoveMax() { // 测试删除最大节点 BST<Integer> bst = new BST<>(); Random random = new Random(); int n = 1000; for (int i = 0; i < n; i++) { bst.add(random.nextInt(10000)); } ArrayList<Integer> nums = new ArrayList<>(); while (!bst.isEmpty()) { nums.add(bst.removeMax()); } // 校验 nums 是否按从大到小的顺序排列 for (int i = 1; i < nums.size(); i++) { if (nums.get(i - 1) < nums.get(i)) { // 如果有一个数比后面的小,则说明删除最大节点的操作的实现是错误的 throw new IllegalArgumentException("removeMax error!"); } } // 运行到此处校验通过 System.out.println("removeMax test completed."); } -
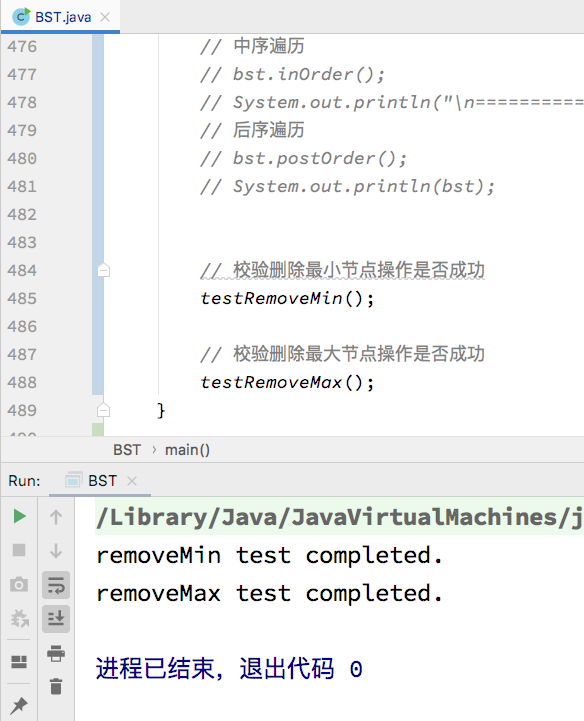
运行结果
-
从运行结果中,可以看出以上实现的两个删除操作都是正确的,接下来就可以实现任意元素的删除了。
删除任意元素
-
对于删除二分搜索树中的任意元素,同样也分为几种情况:删除只有左孩子的节点、删除只有右孩子的节点、删除左右都有孩子的节点。
-
对于前面两种情况:删除只有左孩子的节点、删除只有右孩子的节点,具体步骤其实和前面的删除最大节点和删除最小节点差不多,也是将删除的节点的左子树或者右子树挂接在这个节点原来的位置,将原来的节点从二分搜索树中脱离出去,所以对于这两种情况的删除,实现起来和前面的基本相同。
-
而对于删除左右都有孩子的节点这种情况,就不能使用前面的法子了,这个时候可以使用 Hibbard 提出的 Hibbard Deketion 原理进行删除。
-
具体步骤是这样的:
- 先将要删除的节点记录为 d,然后从 d 的右子树中找到子树中最小的节点用 s 记录下来,这个 s 也就是 d 的后继节点。
- 然后将 d 的右子树中删除掉最小的节点,也就是 s,并将删除 s 后的这个右子树的根赋值给 s 的右节点。也就是 s 从右子树中最小的位置移到了根的位置。
- 接着再将 d 的左子树赋值给 s 的左子树。
- 最后将 d 从二分搜索树中脱离出来,将 s 接到 d 的位置。此时,d 就从树中删除掉了。
-
以上步骤简单来说就是 d 的右子树的节点都是大于 d 的,而其中的最小节点就是排在它后面的节点,此时如果将这个 s 放到 d 的位置,这个 s 节点的左子树依然满足都小于它的特性、同样右子树也满足都大于它的特性,此时就可以达到删除 d 的效果了。
-
同理,也可以在 d 的左子树中找它的前驱,也就是左子树中最大的节点,用 p 记录下来,再将这个 p 按照以上操作 s 的原理将 p 放置到 d 的位置,也可以达成删除 d 的效果。这里就不实现这个找前驱的操作了,实现找后继 s 的操作来删除 d。
-
对于以上删除的步骤,表示为图为以下所示:
- 删除只有左孩子的节点示例:
- 删除只有右孩子的节点示例:
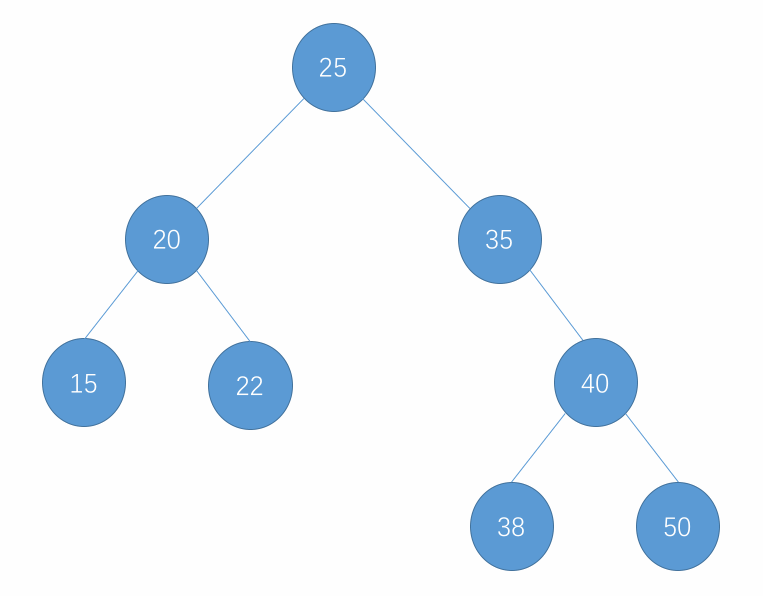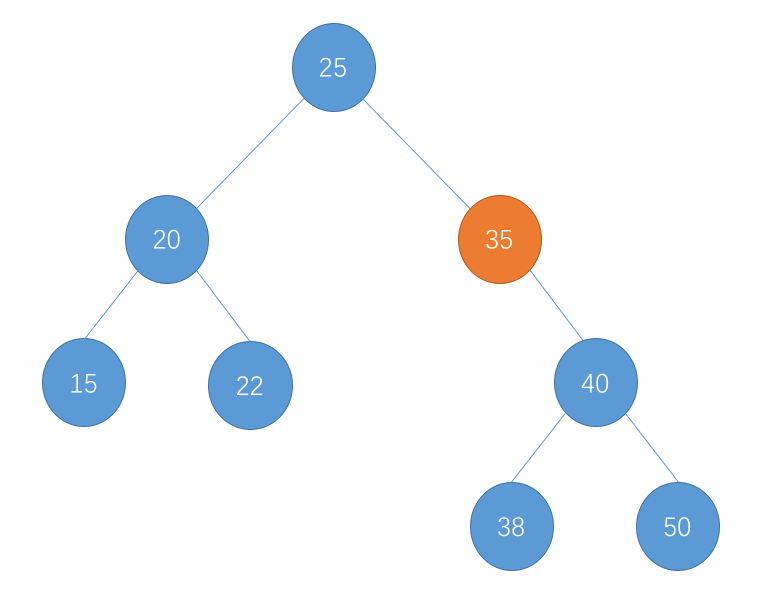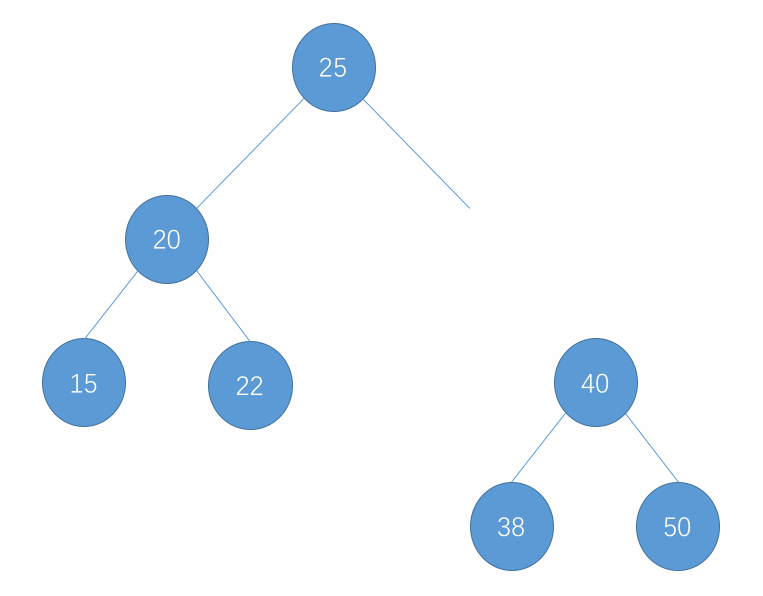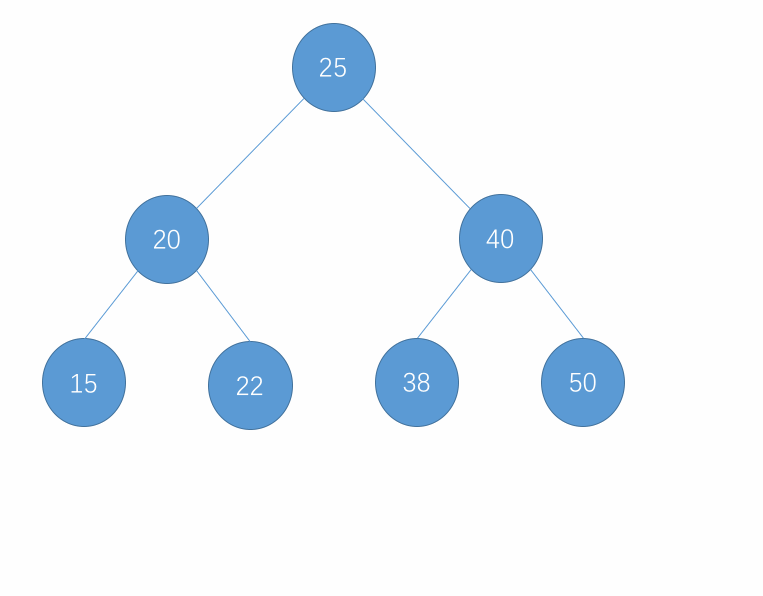
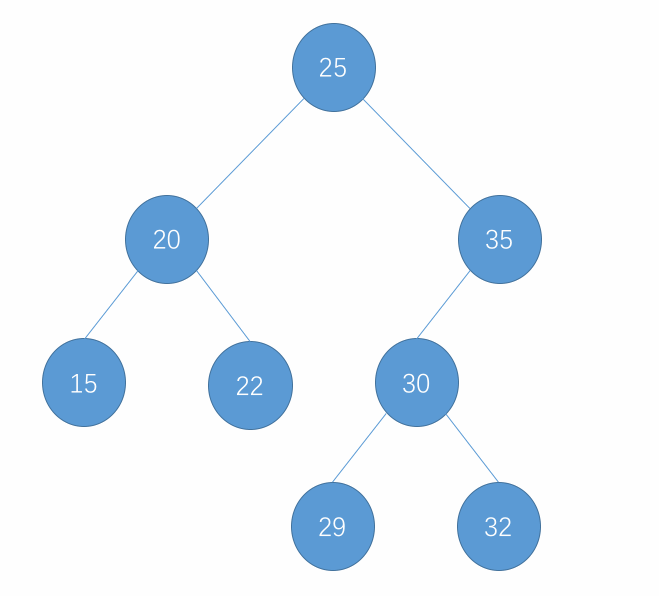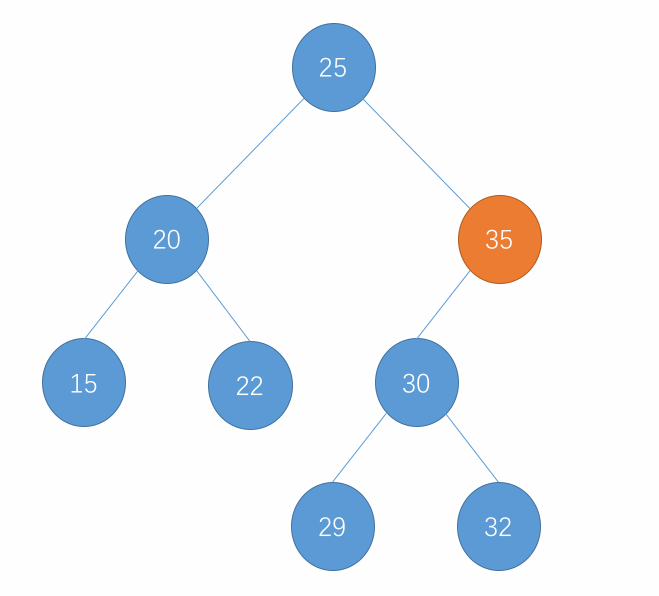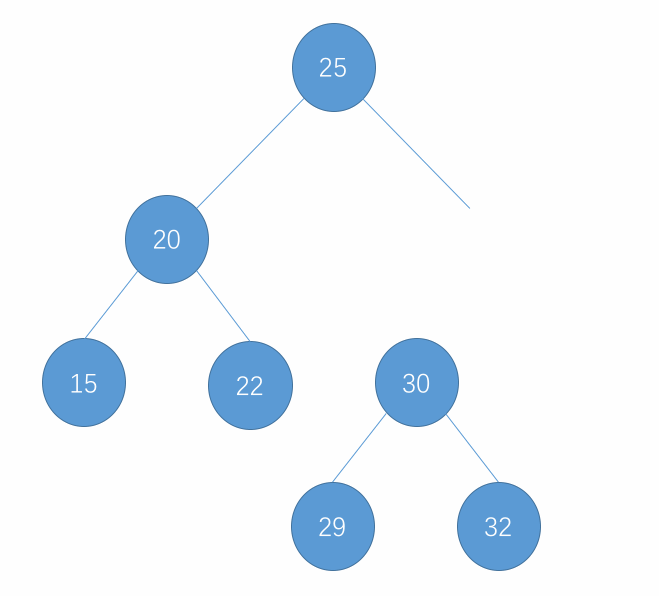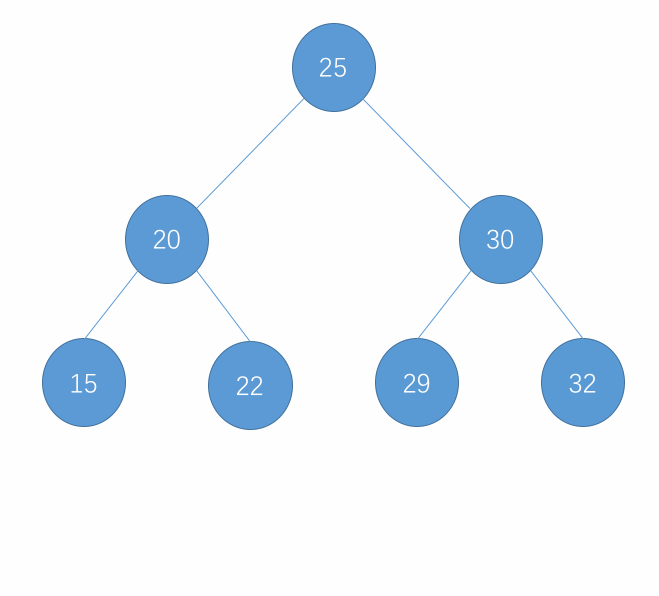
- 删除左右孩子均有的节点示例:
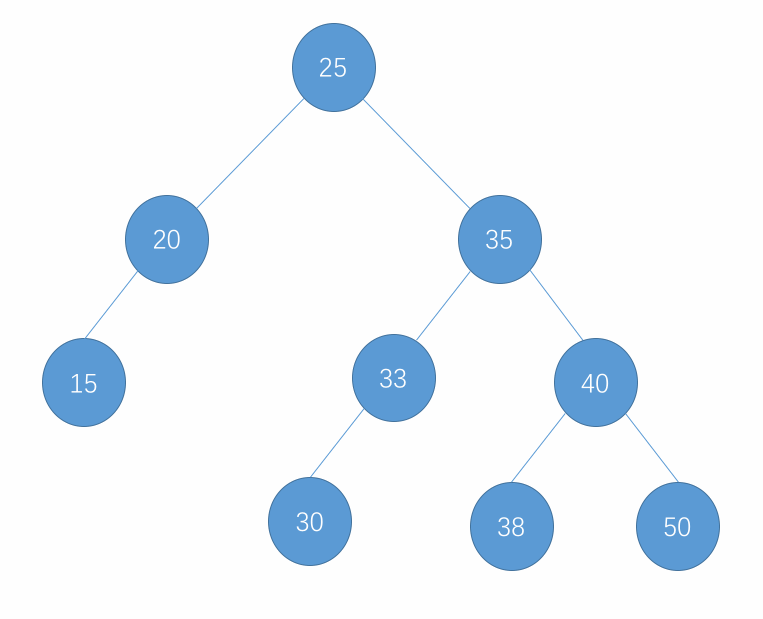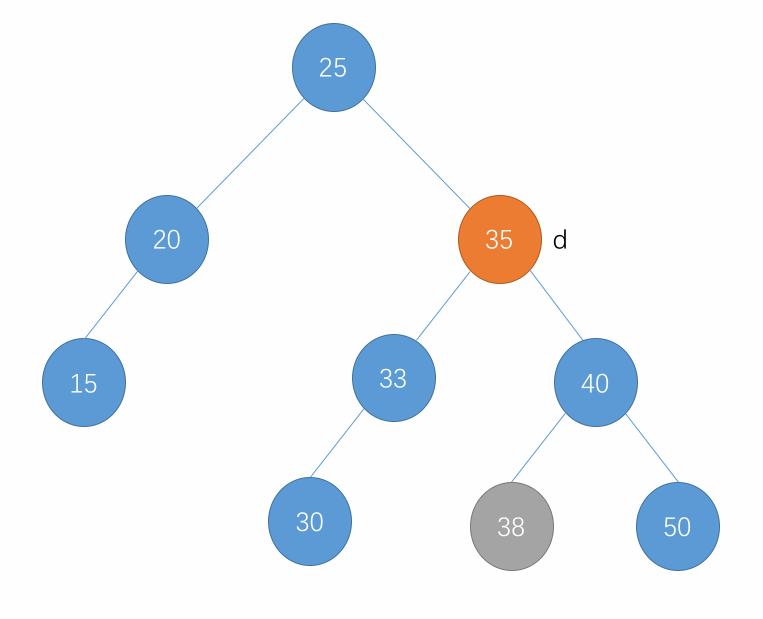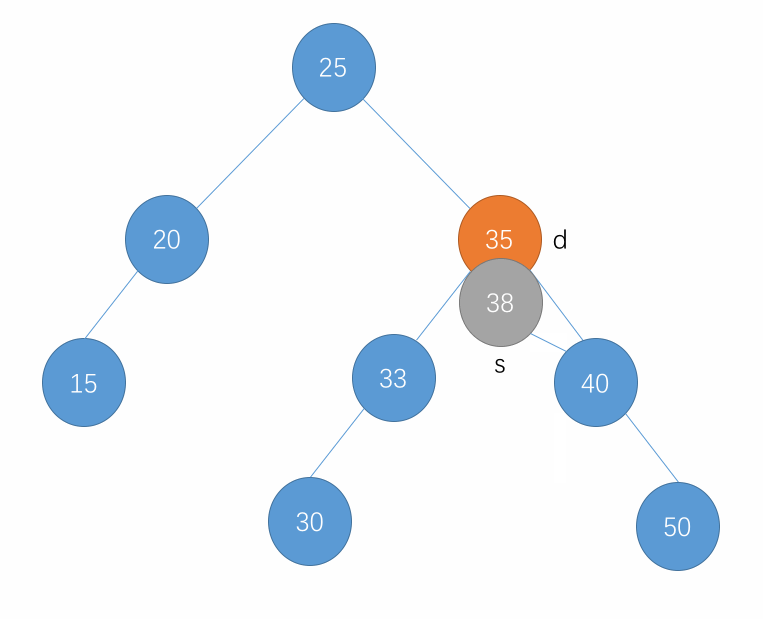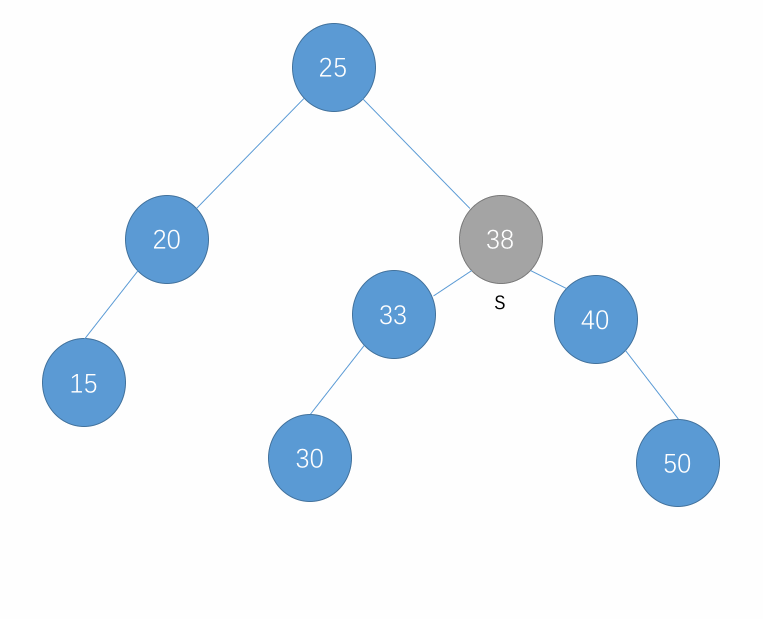
- 删除只有左孩子的节点示例:
-
代码实现如下:
/** * 从二分搜索树中删除元素为 element 的节点 * @param element 要从二分搜索树中删除的元素 */ public void remove(E element) { root = remove(root, element); } /** * 删除以 node 为根的二分搜索树中值为 element 的节点 * 递归函数 * @param node 要删除元素的二分搜索树的根节点 * @param element 要删除的元素 * @return 返回删除节点后新的二分搜索树的根 */ private Node remove(Node node, E element) { if (node == null) { // 如果根节点为空,没有要删除的元素,返回 null 即可 return null; } if (element.compareTo(node.element) < 0) { // 如果要删除的元素比当前根节点的元素小,在左子树中继续寻找 element 进行删除,并使用当前根节点的左节点接收结果 node.left = remove(node.left, element); // 删除后返回当前根节点给上层节点接收 return node; } else if (element.compareTo(node.element) > 0) { // 如果要删除的元素比当前根节点的元素大,在右子树中继续寻找 element 进行删除,并使用当前根节点的右节点接收结果 node.right = remove(node.right, element); // 删除后返回当前根节点给上层节点接收 return node; } else { // 当前根节点的元素为 element,进行删除,三种情况 // 当前删除节点只有右子树 if (node.left == null) { Node rightNode = node.right; node.right = null; size--; return rightNode; } // 当前删除节点只有左子树 if (node.right == null) { Node leftNode = node.left; node.left = null; size--; return leftNode; } // 当前删除节点左右子树均不为空 // 找到当前删除节点大的最小节点,即删除节点右子树的最小节点 // 用这个最小节点代替删除节点的位置 Node successor = minimum(node.right); // 将右子树的最小节点移动到右子树的根位置 successor.right = removeMin(node.right); // 将最小节点的左子树赋为删除节点的左子树 successor.left = node.left; // 将删除节点和二分搜索树脱离 node.left = node.right = null; // 返回 successor 给上层节点接收,顶替 node 的位置,将 node 删除掉 return successor; } } -
实现完之后,也对此测试一下,以验证代码的正确性,测试代码如下:
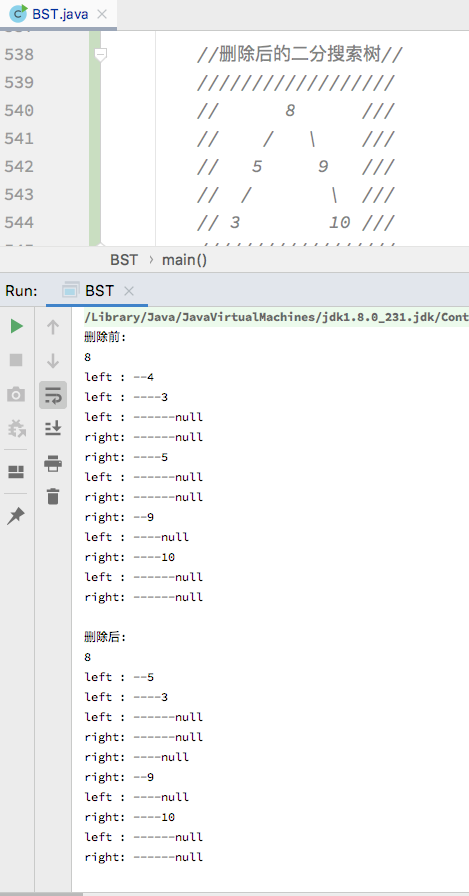
/** * 测试 BST */ public static void main(String[] args) { BST<Integer> bst = new BST<>(); int[] nums = {8, 4, 9, 10, 5, 3}; for (int num : nums) { bst.add(num); } System.out.println("删除前: "); System.out.println(bst); //形成的二分搜索树// ///////////////// // 8 // // / / // // 4 9 // // / / / // // 3 5 10 // ///////////////// // 删除 4 所在的节点 bst.remove(4); //删除后的二分搜索树// ////////////////// // 8 /// // / / /// // 5 9 /// // / / /// // 3 10 /// ////////////////// System.out.println("删除后: "); System.out.println(bst); // 层序遍历 // bst.levelOrder(); // 前序遍历 // bst.preOrder(); // System.out.println("/n==========/n"); // 非递归前序遍历 // bst.preOrederNotRecursive(); // 中序遍历 // bst.inOrder(); // System.out.println("/n==========/n"); // 后序遍历 // bst.postOrder(); // System.out.println(bst); // 校验删除最小节点操作是否成功 // testRemoveMin(); // 校验删除最大节点操作是否成功 // testRemoveMax(); } -
运行结果
-
从运行结果,可以看出是符合预期的,验证了代码编写正确。至此,二分搜索树的这几种操作就都实现完成了。
-
如有写的不足的,还请见谅,也请大家多多指教。(*^▽^*)











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

