Java Collections Framework 源码分析(5.2 - TreeMap, 红黑树的插入)

上一篇文章中我们介绍了 Map ， TreeMap 的接口和内部的数据结构实现：红黑树的概念。今天文章的主要内容是介绍红黑树的核心操作之一，插入操作的代码实现。

在开始本文之前请确认自己掌握了 上一篇文章 中提及的相关知识，即平衡二叉树，Color Flip，Left/Right Rotation 。

平衡二叉树的插入

在上一篇文章中介绍了平衡二叉树的概念，这是一种经过排序的数据结构，那么它的插入逻辑是怎么样的呢？让我们对照 TreeMap 的代码看一下。

TreeMap 通过 put 方法向容器内添加元素， put 方法的开始如下：

public V put(K key, V value) {
    Entry<K,V> t = root;
    if (t == null) {
        compare(key, key); // type (and possibly null) check

        root = new Entry<>(key, value, null);
        size = 1;
        modCount++;
        return null;
    }
......

方法签名很容易理解，就是需要添加的 key 与 value，都是泛型。一开始的 if 判断当前红黑树的根节点是否为空，如果为空的话就将当前添加的数据作为根节点。

如果当前根节点不为空，说明已经有了红黑树的数据结构，则会执行插入的逻辑，让我们继续往下看。

int cmp;
Entry<K,V> parent;
// split comparator and comparable paths
Comparator<? super K> cpr = comparator;
if (cpr != null) {
    do {
        parent = t;
        cmp = cpr.compare(key, t.key);
        if (cmp < 0)
            t = t.left;
        else if (cmp > 0)
            t = t.right;
        else
            return t.setValue(value);
    } while (t != null);
}

这部分主要是检查是否通过构造函数定义了 Comparator 对象，用以定义 key 的比较逻辑。如果你看下以下 if 对应的 else 分支，就会发现其实插入的逻辑都是相同的，因此我们就分析 if 分支。

很容易看到插入的核心逻辑在 do...while 循环中，通过 compare 方法来比较 key 的大小。通过 parent 作为临时变量保存遍历树节点的当前节点的父节点。如果 key 小于当前节点的则向左遍历，否则向右，如果相等则直接将当前节点的值设为最新的 value。

当满足循环终止的条件，即 t == null 时， t 变量肯定是 null ，而 parent 则指向 t 的父节点，此时程序已经找到在树中需要插入节点的位置。

接着就可以执行真正的插入操作，接着往下看。

Entry<K,V> e = new Entry<>(key, value, parent);
if (cmp < 0)
    parent.left = e;
else
    parent.right = e;
fixAfterInsertion(e);

很简单，通过 key 和 value 初始化 Entry 这是上一篇文章提到的红黑树节点的数据结构。然后按照比较结果的大小，设置插入的节点为左节点还是右节点。到这里平衡二叉树插入的程序就结束了，很简单吧。而关键的是在 fixAfterInsertion 这个方法中，确认自己明白了插入逻辑后，再继续往下看。

红黑树插入后的调整

从上面的代码可以看出数据插入后有可能不再符合平衡二叉树的定义，因此需要调整插入后节点的位置。同时 TreeMap 中使用的是红黑树结构，所以调整后的树状结构也应该符合红黑树的定义，而这部分的功能就是在 fixAfterInsertion 中。在阅读 fixAfterInsertion 的源码之前，先让我们了解一下红黑树插入后调整的算法。

插入后调整

这部分的算法在 wikipedia 上的描述很简答，也易于理解，所以我引用 wikipedia 的描述来解释这部分算法。

为了之后描述方便，我们定义几种节点类型和对应的缩写，具体如下：

• 当前节点： N
• 当前节点的父节点： P
• 当前节点的的兄弟节点，即当前节点父节点的另一个子节点： S
• 当前节点父节点的兄弟节点，也称之为“叔叔”节点： U
• 当前节点的父节点的父节点，也称之为“祖父”节点： G

下面这幅图解释了各种节点类型的位置，请确认自己的理解正确，再接续。

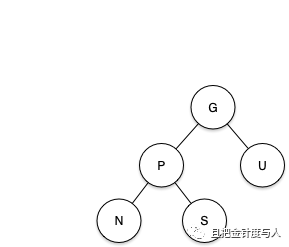
首先按照插入节点的不同情况进行对应的处理，具体分为以下 4 种状态：

1. N 为根节点
2. P 为 黑色 节点
3. P 为 红色 ，而 U 也为 红色
4. P 为 红色 ，而 U 不为 红色

这 4 种状态的处理其实非常简单，你最终发现其实只需要记住如何处理第 3，第 4 种状态就行了。让我们开始吧。

第 1 种状态非常简单，作为根节点需要做的就是将当前节点的颜色变为黑色即可，其他什么都不用做。

第 2 种状态更简单，你什么都不用做 ^o^，只需要保证当前插入节点的颜色为红色即可。

第 3 种状态则需要做一些操作。还记得 Color Flip 操作吗？要做的第一步是对 G 节点做 Color Flip 操作，即将 G 节点变为红色， P 和 U 节点变为黑色。第二步是将 G 作为参数再次执行调整算法 ，可以看作是个递归调用。

第 4 种状态是最为复杂的一种，分为两个阶段，但总体来说也很容易理解，放松心情往下看。

1. 对 **P** 进行 Rotation
    1. 如果 **N** 为 **P**  右节点，且 **P** 为 **G** 的左节点，则对 **P** 进行 Left Rotation
    2. 如果 **N** 为 **P** 的左节点，且 **P** 为 **G** 的右节点，则对 **P** 进行 Right Rotation
    3. 如果不满足上述的条件则什么都不做
2. 对 **G** 进行 Rotation 
    1. 如果 **N** 为 **P**  右节点，则对 **G** 进行 Left Rotation
    2. 如果 **N** 为 **P**  左节点，则对 **G** 进行 Right Rotation
    3. 将 **P** 的颜色变为**黑色**
    4. 将 **G** 变为**红色**

fixAfterInsertion 源码

先看一下 fixAfterInsertion 的源码：

/** From CLR */
private void fixAfterInsertion(Entry<K,V> x) {
    x.color = RED;

    while (x != null && x != root && x.parent.color == RED) {
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateLeft(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);
                setColor(y, BLACK);
                setColor(parentOf(parentOf(x)), RED);
                x = parentOf(parentOf(x));
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);
                    rotateRight(x);
                }
                setColor(parentOf(x), BLACK);
                setColor(parentOf(parentOf(x)), RED);
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    root.color = BLACK;
}

这部分算法的实现来自于大名鼎鼎，大部分人半途而废的算法名著：<<算法导论>>，即注释中的 CLR(CLR 是算法导论 3 位作者名称的缩写)。

在开始阶段会将节点的颜色设置为红色，然后开始循环。循环条件很简单，当前节点为不为空，当前节点不为根节点，当前节点父节点的颜色为红色。其实分析一下这个条件就可看到已经覆盖了之前 4 种情况的第 1 ，第 2 种情况了。

接着看 if 分支的条件， if (parentOf(x) == leftOf(parentOf(parentOf(x)))) ，即 P 是 G 的左节点。紧接着的 Entry<K,V> y = rightOf(parentOf(parentOf(x))); 是获取 U 节点，即父节点的兄弟节点。然后判断 U 节点的颜色是否为红色。这时对照我们提到的 4 种状态，你会发现此时程序的状态已经满足第 3 种状态了，即 P 为 红色 ， U 也为红色。接着让我们看看，在这种分支下的处理逻辑：

if (colorOf(y) == RED) {
    setColor(parentOf(x), BLACK);
    setColor(y, BLACK);
    setColor(parentOf(parentOf(x)), RED);
    x = parentOf(parentOf(x));
}

一开始的 3 行的三行就是 Color Flip 的操作，将 G 设为 红色 ， P 与 U 设为 黑色 ，然后将 x 指向 G ，开始下一轮的循环。这完全符合我们提到第 3 种情况的算法逻辑。

接着看对应的 else 分支代码。

else {
    if (x == rightOf(parentOf(x))) {
        x = parentOf(x);
        rotateLeft(x);
    }
    setColor(parentOf(x), BLACK);
    setColor(parentOf(parentOf(x)), RED);
    rotateRight(parentOf(parentOf(x)));
}

这个分支走的就是我们提及的第 4 种状态的分支了。同样的，此时 P 是 G 的左节点，然后 x == rightOf(parentOf(x)) 是检查 N 是否为 P 的右节点。满足该条件的话，按照第 4 种状态的第 1 阶段算法，应该将 P 节点做 Left Rotation，代码中也是如此做的。之后的三行代码：

setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);
rotateRight(parentOf(parentOf(x)));

就是第 4 种状态的第 2 阶段操作：设置 P 和 G 的颜色，并对 G 进行 Rotation。

对应最外层 if 分支的 else 分支的代码其实大部分是一样的，只是 rotation 旋转的方向不同，对应第 4 种情况的另外一个分支，我就不在解释，留给你自己从代码对应算法描述了。

小结

本次文章结合 TreeMap 的代码解释了红黑树插入和重新平衡的操作，大家可以认真的对照代码和算法描述理清思路，了解红黑树的数据结构特点和算法，下一篇文章会介绍红黑树的删除操作，这也是 TreeMap 和红黑树的最后一篇了，希望这 3 篇文章能够让你真正掌握红黑树的算法。

欢迎关注我的微信号「且把金针度与人」,获取更多高质量文章