老大说：谁要再用double定义商品金额，就自己收拾东西走
先看现象
涉及诸如 float 或者 double 这两种浮点型数据的处理时，偶尔总会有一些 怪怪的现象 ，不知道大家注意过没，举几个常见的栗子：
典型现象（一）：条件判断超预期
System.out.println( 1f == 0.9999999f ); // 打印：false System.out.println( 1f == 0.99999999f ); // 打印：true 纳尼？
典型现象（二）：数据转换超预期
float f = 1.1f; double d = (double) f; System.out.println(f); // 打印：1.1 System.out.println(d); // 打印：1.100000023841858 纳尼？
典型现象（三）：基本运算超预期
System.out.println( 0.2 + 0.7 ); // 打印：0.8999999999999999 纳尼？
典型现象（四）：数据自增超预期
float f1 = 8455263f;
for (int i = 0; i < 10; i++) {
System.out.println(f1);
f1++;
}
// 打印：8455263.0
// 打印：8455264.0
// 打印：8455265.0
// 打印：8455266.0
// 打印：8455267.0
// 打印：8455268.0
// 打印：8455269.0
// 打印：8455270.0
// 打印：8455271.0
// 打印：8455272.0
float f2 = 84552631f;
for (int i = 0; i < 10; i++) {
System.out.println(f2);
f2++;
}
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
// 打印：8.4552632E7 纳尼？不是 +1了吗？
看到没，这些简单场景下的使用情况都很难满足我们的需求，所以说用浮点数（包括 double 和 float ）处理问题有非常多 隐晦的坑 在等着咱们！
怪不得技术总监发狠话：谁要是敢在处理诸如 商品金额 、 订单交易 、以及 货币计算 时用浮点型数据（ double / float ），直接让我们走人！
原因出在哪里？
我们就以第一个典型现象为例来分析一下：
System.out.println( 1f == 0.99999999f );
直接用代码去比较 1 和 0.99999999 ，居然打印出 true ！
这说明了什么？这说明了计算机压根 区分不出来 这两个数。这是为什么呢？
我们不妨来简单思考一下：
我们知道输入的这两个浮点数只是我们人类肉眼所看到的具体数值，是我们通常所理解的十进制数，但是计算机底层在计算时可不是按照十进制来计算的，学过基本计组原理的都知道，计算机底层最终都是基于像 010100100100110011011 这种 0 、 1 二进制来完成的。
所以为了搞懂实际情况，我们应该将这两个十进制浮点数 转化到二进制空间 来看一看。
十进制浮点数转二进制怎么转、怎么计算，我想这应该属于基础计算机进制转换常识，在 《计算机组成原理》 类似的课上肯定学过了，咱就不在此赘述了，直接给出结果（把它转换到 IEEE 754 Single precision 32-bit ，也就 float 类型对应的精度）
1.0（十进制）
↓
00111111 10000000 00000000 00000000（二进制）
↓
0x3F800000（十六进制）
0.99999999（十进制）
↓
00111111 10000000 00000000 00000000（二进制）
↓
0x3F800000（十六进制）
果不其然，这两个十进制浮点数的底层二进制表示是一毛一样的，怪不得 == 的判断结果返回 true ！
但是 1f == 0.9999999f 返回的结果是符合预期的，打印 false ，我们也把它们转换到二进制模式下看看情况：
1.0（十进制）
↓
00111111 10000000 00000000 00000000（二进制）
↓
0x3F800000（十六进制）
0.9999999（十进制）
↓
00111111 01111111 11111111 11111110（二进制）
↓
0x3F7FFFFE（十六进制）
哦，很明显，它俩的二进制数字表示确实不一样，这是理所应当的结果。
那么为什么 0.99999999 的底层二进制表示竟然是： 00111111 10000000 00000000 00000000 呢？
这不明明是浮点数 1.0 的二进制表示吗？
这就要谈一下浮点数的精度问题了。
浮点数的精度问题！
学过 《计算机组成原理》 这门课的小伙伴应该都知道，浮点数在计算机中的存储方式遵循 IEEE 754 浮点数计数标准 ，可以用科学计数法表示为：
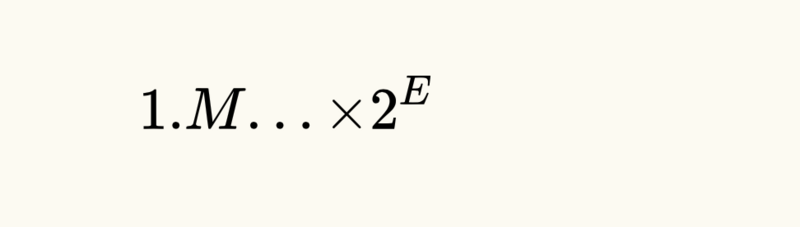
只要给出： 符号（S） 、 阶码部分（E） 、 尾数部分（M） 这三个维度的信息，一个浮点数的表示就完全确定下来了，所以 float 和 double 这两种浮点数在内存中的存储结构如下所示：
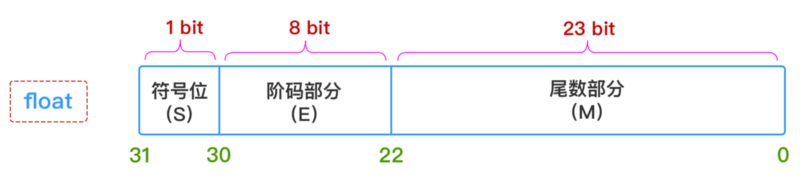
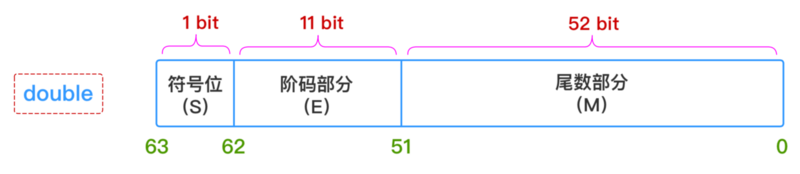
1、符号部分（S）
0 -正 1 -负
2、阶码部分（E）（指数部分）：
- 对于
float型浮点数，指数部分8位，考虑可正可负，因此可以表示的指数范围为-127 ~ 128 - 对于
double型浮点数，指数部分11位，考虑可正可负，因此可以表示的指数范围为-1023 ~ 1024
3、尾数部分（M）：
浮点数的精度是由尾数的位数来决定的：
- 对于
float型浮点数，尾数部分23位，换算成十进制就是2^23=8388608，所以十进制精度只有6 ~ 7位； - 对于
double型浮点数，尾数部分52位，换算成十进制就是2^52 = 4503599627370496，所以十进制精度只有15 ~ 16位
所以对于上面的数值 0.99999999f ，很明显已经超过了 float 型浮点数据的精度范围，出问题也是在所难免的。
精度问题如何解决
所以如果涉及 商品金额 、 交易值 、 货币计算 等这种对精度要求很高的场景该怎么办呢？
方法一：用字符串或者数组解决多位数问题
校招刷过算法题的小伙伴们应该都知道，用字符串或者数组表示大数是一个典型的解题思路。
比如经典面试题： 编写两个任意位数大数的加法、减法、乘法等运算 。
这时候我们我们可以用字符串或者数组来表示这种大数，然后按照四则运算的规则来手动模拟出具体计算过程，中间还需要考虑各种诸如： 进位 、 借位 、 符号 等等问题的处理，确实十分复杂，本文不做赘述。
方法二：Java的大数类是个好东西
JDK早已为我们考虑到了浮点数的计算精度问题，因此提供了专用于高精度数值计算的 大数类 来方便我们使用。
在前文 《不瞒你说，我最近跟Java源码杠上了》 中说过，Java的大数类位于 java.math 包下：
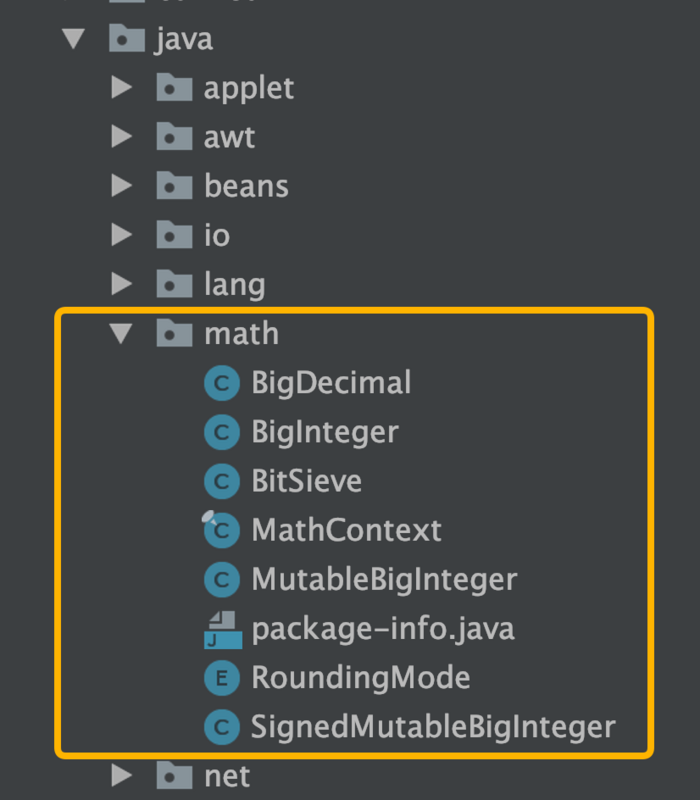
可以看到，常用的 BigInteger 和 BigDecimal 就是处理高精度数值计算的利器。
BigDecimal num3 = new BigDecimal( Double.toString( 0.1f ) ); BigDecimal num4 = new BigDecimal( Double.toString( 0.99999999f ) ); System.out.println( num3 == num4 ); // 打印 false BigDecimal num1 = new BigDecimal( Double.toString( 0.2 ) ); BigDecimal num2 = new BigDecimal( Double.toString( 0.7 ) ); // 加 System.out.println( num1.add( num2 ) ); // 打印：0.9 // 减 System.out.println( num2.subtract( num1 ) ); // 打印：0.5 // 乘 System.out.println( num1.multiply( num2 ) ); // 打印：0.14 // 除 System.out.println( num2.divide( num1 ) ); // 打印：3.5
当然了，像 BigInteger 和 BigDecimal 这种大数类的运算效率肯定是不如原生类型效率高，代价还是比较昂贵的，是否选用需要根据实际场景来评估。
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
