高级数据结构---红黑树及其插入左旋右旋代码java实现
前面我们说到的二叉查找树,可以看到根结点是初始化之后就是固定了的,后续插入的数如果都比它大,或者都比它小,那么这个时候它就退化成了链表了,查询的时间复杂度就变成了 O(n), 而不是理想中 O(logn), 就像这个样子
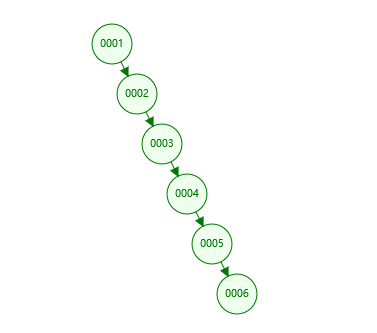
如果我们有一个平衡机制,让这棵树可以动起来,比如将 4 变成根结点,是不是查询效率又可以提高了,这就要提到另外一种特殊的二叉树 --- 红黑树(也是一种特殊的二叉查找树)。 JDK1.8 中将 HashMap 底层实现的数据结构由数组 + 链表变成了数组 + 链表 + 红黑树。当链表长度超过 8 就转换成红黑树,明显红黑树的查找效率是高于链表的吧。
红黑树的特点:
1. 每个结点不是红色就是黑色
2. 不可能有连在一起的红色结点(黑色的就可以),每个叶子节点都是黑色的空节点( nil ),也就是说,叶子节点不存储数据
3. 根结点都是黑色 root
4. 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
5. 新插入的元素都是红色,根除外
因为红黑树要满足以上特点,所以就有 变色机制和旋转平衡机制 来调节树高度。
变色:
当前节点红色,父结点和叔叔结点都是红色,将父结点和叔叔结点变成黑色,把爷爷结点设置成红色;只有父结点是红色,那就将父结点变黑色,爷爷结点变红色。完成变色之后进行左旋 / 右旋。
注:下面的 当前节点都是变化后的操作结点 。
左旋: 变完色之后将操作结点变成爷爷结点,以其爷爷结点去旋转。
条件:当前结点(爷爷结点)父结点是红色,叔叔是黑色,且当前结点是右子树。
操作结点指向父结点,将当前结点(变色前结点的太爷爷)右孩子的左孩子变成其右孩子,当前结点变成其右孩子的左孩子,其右孩子填补当前结点位置
右旋:
条件:当前结点父结点是红色,叔叔是黑色,且当前结点是左子树。
父结点变成黑色,爷爷变成红色 (这个变色就是上面的第二种变色) ,以太爷爷为 操作结 点右旋。将其左孩子的右子树变成其左子树,将当前结点变成其左孩子的右子树。其做孩子填补当前位置 。
左旋右旋动图:

代码实现:真心的太抽象了,看起来简单,代码实现起来,各种结点的引用指向太乱了;下面的代码几乎每一行都写了注释,尤其是左旋和右旋
package com.nijunyang.algorithm.tree;
/**
* Description: 红黑树
* Created by nijunyang on 2020/4/20 20:23
*
* 红黑树的性质:
* 1.每个结点不是红色就是黑色
* 2.不可能有连在一起的红色结点(黑色的就可以),每个叶子节点都是黑色的空节点(nil),也就是说,叶子节点不存储数据
* 3.根结点都是黑色 root
* 4.每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点
* 5.新插入的元素都是红色,根除外
*/
public class RedBlackTree {
private Node root = Node.nil;
public static void main(String[] args){
RedBlackTree redBlackTree = new RedBlackTree();
//19,5,30,1,12,35,7,13,6
redBlackTree.insert(19);
redBlackTree.insert(5);
redBlackTree.insert(30);
redBlackTree.insert(1);
redBlackTree.insert(12);
redBlackTree.insert(35);
redBlackTree.insert(7);
redBlackTree.insert(13);
redBlackTree.insert(6);
RedBlackTree.inOrderTraversal(redBlackTree);
System.out.println();
}
public <T extends Comparable<T>> void insert(T data){
Node<T> temp = root;
Node<T> node = new Node<>(data);
if (root == Node.nil) {
root = node;
node.parent.parent = Node.nil;
}
else {
node.black = false;
//插入
while (true) {
if (temp.data.compareTo(data) < 0) {
if (temp.rightChild == Node.nil) {
temp.rightChild = node;
node.parent = temp;
break;
} else {
temp = temp.rightChild;
}
}
else if (temp.data.compareTo(data) == 0) {
//等于保留原来数据
return;
}
else {
if (temp.leftChild == Node.nil) {
temp.leftChild = node;
node.parent = temp;
break;
} else {
temp = temp.leftChild;
}
}
}
//变色和旋转
fixTree(node);
}
}
private static void inOrderTraversal(RedBlackTree redBlackTree) {
TreeUtil.inOrderTraversal(redBlackTree.root);
}
/**
* 变色和旋转
* @param node
* @param <T>
*/
private <T extends Comparable<T>> void fixTree(Node<T> node) {
/**
* 1.变色 条件:父结点及叔叔结点都是红色,变色过程:把父结点和叔叔结点都变成黑色,把爷爷设置成红色,指针指向爷爷结点
* 2.左旋:上一步将指针指向了爷爷结点.条件:当前结点(爷爷结点)父结点是红色,叔叔是黑色,且当前结点是右子树。进行左旋:
* 临时指针指向父结点,将当前结点(变色前结点的太爷爷)右孩子的左孩子变成其右孩子,当前结点变成其右孩子的左孩子,
* 其右孩子填补当前结点位置
*
* 3.右旋:条件:当前结点父结点是红色,叔叔是黑色,且当前结点是左子树。进行右旋:
* 父结点变成黑色,爷爷变成红色,以太爷爷为点右旋。将其左孩子的右子树变成其左子树,将当前结点变成其左孩子的右子树。其做孩子填补当前位置
*
*/
Node<T> currentNode = node;
while (!currentNode.parent.black) {
Node<T> temp;
if (currentNode.parent == currentNode.parent.parent.leftChild) { //当前父结点是左孩子
temp = currentNode.parent.parent.rightChild; //叔叔结点
//变色
if (temp != Node.nil && !temp.black) { //叔叔也是红色,将父和叔叔都变黑色
currentNode.parent.black = true;
temp.black = true;
currentNode.parent.parent.black = false; //爷爷变成红色
currentNode = currentNode.parent.parent; //变色完成指向爷爷
continue; //进入下一次循环判断爷爷的位置是否也需要变色,直到不变满足变色了才开始左旋/右旋
}
if (currentNode == currentNode.parent.rightChild) { //当前结点是右子树
currentNode = currentNode.parent; //以其父结点进行左旋
//左旋
leftRotate(currentNode);
}
//右旋
//父结点变成黑色,爷爷变成红色,准备右旋
currentNode.parent.black = true;
currentNode.parent.parent.black = false;
//指针指向太爷爷去右旋
currentNode = currentNode.parent.parent;
rightRotate(currentNode);
}
else { //当前父结点是右孩子
temp = currentNode.parent.parent.leftChild;
if (temp != Node.nil && !temp.black) {
currentNode.parent.black = true;
temp.black = true;
currentNode.parent.parent.black = false;
currentNode = currentNode.parent.parent;
continue;
}
if (currentNode == currentNode.parent.leftChild) {
currentNode = currentNode.parent;
rightRotate(currentNode);
}
//父结点变成黑色,爷爷变成红色,准备左旋
currentNode.parent.black = true;
currentNode.parent.parent.black = false;
//指针指向太爷爷去左旋
currentNode = currentNode.parent.parent;
leftRotate(currentNode);
}
}
root.black = true; //根结点始终黑色
}
/**
* 左旋:将其右孩子的左孩子变成其右孩子,当前结点变成其右孩子的左孩子,其右孩子填补当前结点位置
* @param node
* @param <T>
*/
private <T extends Comparable<T>> void leftRotate(Node<T> node) {
Node <T> currentNode = node;
if (currentNode.parent != Node.nil) {
if (currentNode == currentNode.parent.leftChild) { //当前结点是其父的左孩子
currentNode.parent.leftChild = currentNode.rightChild; // 将其右孩子变成其父的左孩子(右孩子填补当前结点位置)
}
else {
currentNode.parent.rightChild = currentNode.rightChild; //将其右孩子变成其父的右孩子(右孩子填补当前结点位置)
}
currentNode.rightChild.parent = currentNode.parent; //修改其右孩子的父指针,移向其父(右孩子填补当前结点位置)
currentNode.parent = currentNode.rightChild; //当前结点变成其右孩子的孩子
if (currentNode.rightChild.leftChild != Node.nil) {
currentNode.rightChild.leftChild.parent = currentNode; //当前结点右孩子的左孩子变成当前结点的孩子,修改父指针
}
currentNode.rightChild = currentNode.rightChild.leftChild; //当前结点右孩子的左孩子变成当前结点的右孩子
currentNode.parent.leftChild = currentNode; //当前结点新的父亲(以前它的右孩子)的左孩子指向当前节点
}
else { //根就是当前结点
Node right = root.rightChild;
root.rightChild = right.leftChild; //将其右孩子的左孩子变成其右孩子
right.leftChild.parent = root; //修改对应的父指向
root.parent = right;
right.leftChild = root; //当前结点变成其右孩子的左孩子
right.parent = Node.nil;
root = right; //右孩子填补当前位置
}
}
/**
* 右旋:父结点变成黑色,爷爷变成红色,准备右旋。将其左孩子的右子树变成其左子树,将当前结点变成其左孩子的右子树。其左孩子填补当前位置,
* 最后当前节点变成其
* @param node node
* @param <T>
*/
private <T extends Comparable<T>> void rightRotate(Node<T> node) {
Node <T> currentNode = node;
if (currentNode.parent != Node.nil) {
if (currentNode == currentNode.parent.leftChild) { //判断当前结点是其父的左/右结点,其左孩子填补当前位置
currentNode.parent.leftChild = currentNode.leftChild;
} else {
currentNode.parent.rightChild = currentNode.leftChild;
}
currentNode.leftChild.parent = currentNode.parent; //其左孩子填补当前位置,左孩子父指针指向其父指针
currentNode.parent = currentNode.leftChild; //当前结点变成其左孩子的子树
if (currentNode.leftChild.rightChild != Node.nil) {
currentNode.leftChild.rightChild.parent = currentNode; //将其左孩子的右子树变成其左子树
}
currentNode.leftChild = currentNode.leftChild.rightChild; //将其左孩子的右子树变成其左子树
currentNode.parent.rightChild = currentNode; //当前结点新的父亲(以前它的左孩子)的右孩子指向当前节点
} else { //当前结点是根结点
Node<T> left = root.leftChild;
root.leftChild = root.leftChild.rightChild; // 将其左孩子的右子树变成其左子树
left.rightChild.parent = root;
root.parent = left;
left.rightChild = root; //将当前结点变成其左孩子的右子树
left.parent = Node.nil;
root = left; //左孩子填补当前位置
}
}
private static class Node<T extends Comparable<T>> extends TreeNode<T> {
private static final Node nil = new Node<>(null);
T data;
Node<T> parent = nil;
Node<T> leftChild = nil;
Node<T> rightChild = nil;
boolean black = true; //默认黑色
public Node(T data) {
this.data = data;
}
@Override
public T getData() {
return data;
}
@Override
public void setData(T data) {
this.data = data;
}
@Override
public Node<T> getLeftChild() {
return leftChild;
}
public void setLeftChild(Node<T> leftChild) {
this.leftChild = leftChild;
}
@Override
public Node<T> getRightChild() {
return rightChild;
}
public void setRightChild(Node<T> rightChild) {
this.rightChild = rightChild;
}
@Override
public String toString() {
return "data=" + data;
}
}
}
中序遍历的代码:
/**
* 二叉树中序遍历 左子树 根 右子树
* @param node 二叉树节点
*/
public static<N extends TreeNode<T>, T> void inOrderTraversal(N node){
if(node == null){
return;
}
//先找左再输出根,再去找右
inOrderTraversal(node.getLeftChild());
if (node.getData() != null) {
System.out.print(node.getData());
System.out.print(" ");
}
inOrderTraversal(node.getRightChild());
}
TreeNode:
public class TreeNode<T> {
protected T data;
protected TreeNode<T> leftChild;
protected TreeNode<T> rightChild;
public TreeNode() {
}
}
在 https://www.cs.usfca.edu/~galles/visualization/RedBlack.html 上面验证了下插入代码的运行结果和这儿的图解结果是一致的。 19,5,30,1,12,35,7,13,6

因为红黑树通过变色和左旋 / 右旋机制使得个子树的高度尽量平衡,所以他的查询效率是 O(logn)。 其插入和删除也是近似 O(logn).











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

