「力扣」第 1080 题:根到叶路径上的不足节点
题解地址: 分治法、后序遍历(Python 代码、Java 代码) 。
说明:文本首发在力扣的题解版块,更新也会在第 1 时间在上面的网站中更新,这篇文章只是上面的文章的一个快照,您可以点击上面的链接看到其他网友对本文的评论。
传送门: 根到叶路径上的不足节点 。
给定一棵二叉树的根 root,请你考虑它所有 从根到叶的路径:从根到任何叶的路径。(所谓一个叶子节点,就是一个没有子节点的节点)
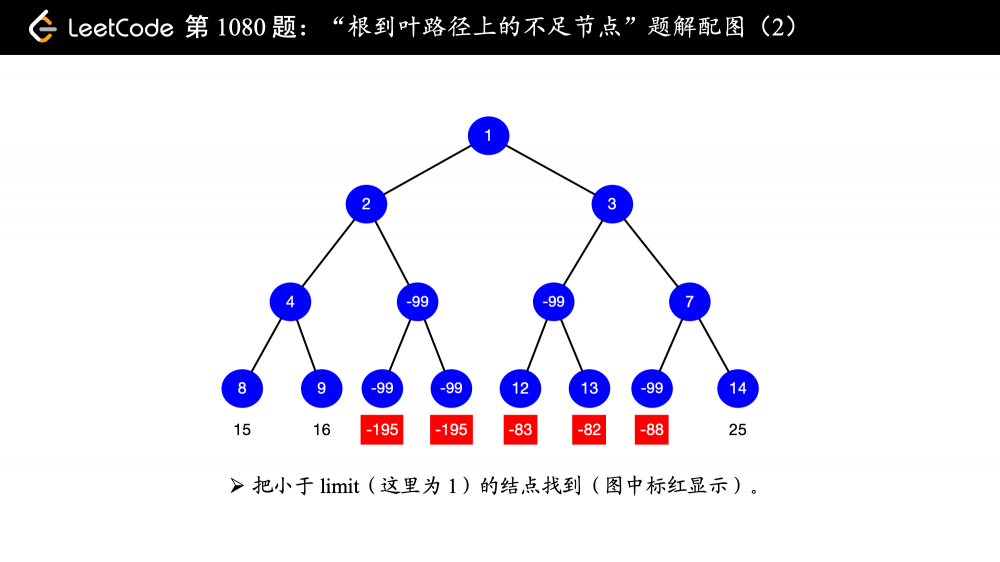
假如通过节点 node 的每种可能的 “根-叶” 路径上值的总和全都小于给定的 limit,则该节点被称之为「不足节点」,需要被删除。
请你删除所有不足节点,并返回生成的二叉树的根。
示例 1:
输入:root = [1,2,3,4,-99,-99,7,8,9,-99,-99,12,13,-99,14], limit = 1
输出:[1,2,3,4,null,null,7,8,9,null,14]
示例 2:
输入:root = [5,4,8,11,null,17,4,7,1,null,null,5,3], limit = 22
输出:[5,4,8,11,null,17,4,7,null,null,null,5]
示例 3:
输入:root = [5,-6,-6], limit = 0
输出:[]
提示:
给定的树有 1 到 5000 个节点
-10^5 <= node.val <= 10^5
-10^9 <= limit <= 10^9
分治法、后序遍历(Python 代码、Java 代码)
首先考虑结点如何删除
首先我们考虑如何删除结点的问题。已知一个二叉树中的结点要被删除,有两种办法:
- 自己删除自己;
- 告诉父亲结点,自己需要从二叉树中被删除。
“自己删除自己” 让我想到了 “单链表删除某个结点”,如果这个要被删除的结点是末尾结点,那还麻烦了。不过第 2 种办法“告诉父亲结点,自己需要从二叉树中被删除”,就很简单了, 父亲结点收到孩子结点这个信号以后,只要把对孩子结点的引用切断即可 。
其次考虑使用哪一种遍历方式
二叉树的问题一定离不开遍历,遍历有 DFS 和 BFS,根据题目中的描述 “考虑它所有 从根到叶的路径”,就知道不能用 BFS 了,那么 DFS 又有 3 种,分别如下:
1、先序遍历
(1)先执行当前结点的逻辑;
(2)如果有左结点,就递归执行左结点的逻辑;
(3)如果有右结点,就递归执行右结点的逻辑。
2、中序遍历
(1)如果有左结点,就递归执行左结点的逻辑;
(2)先执行当前结点的逻辑;
(3)如果有右结点,就递归执行右结点的逻辑。
3、后序遍历
(1)如果有左结点,就递归执行左结点的逻辑;
(2)如果有右结点,就递归执行右结点的逻辑;
(3)先执行当前结点的逻辑。
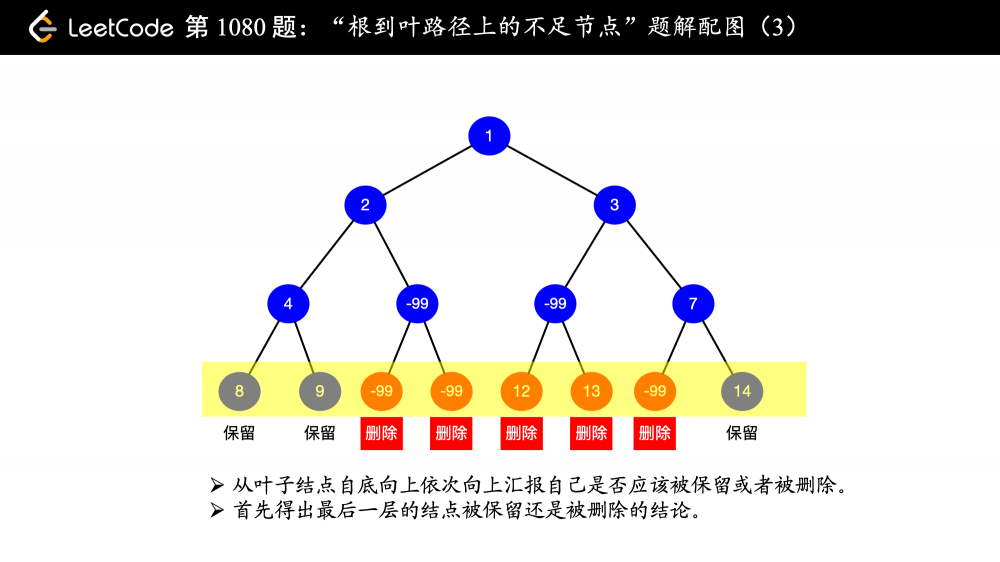
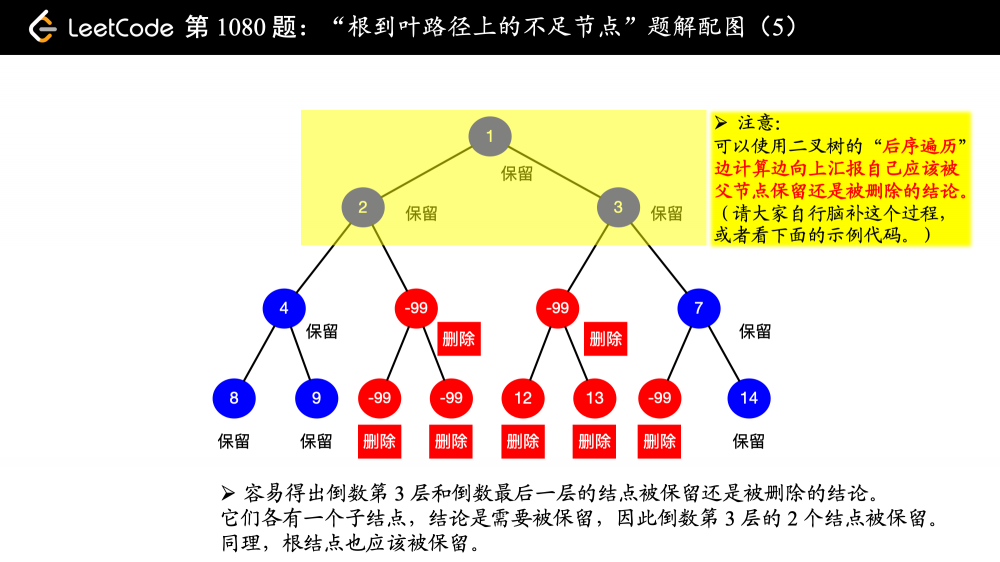
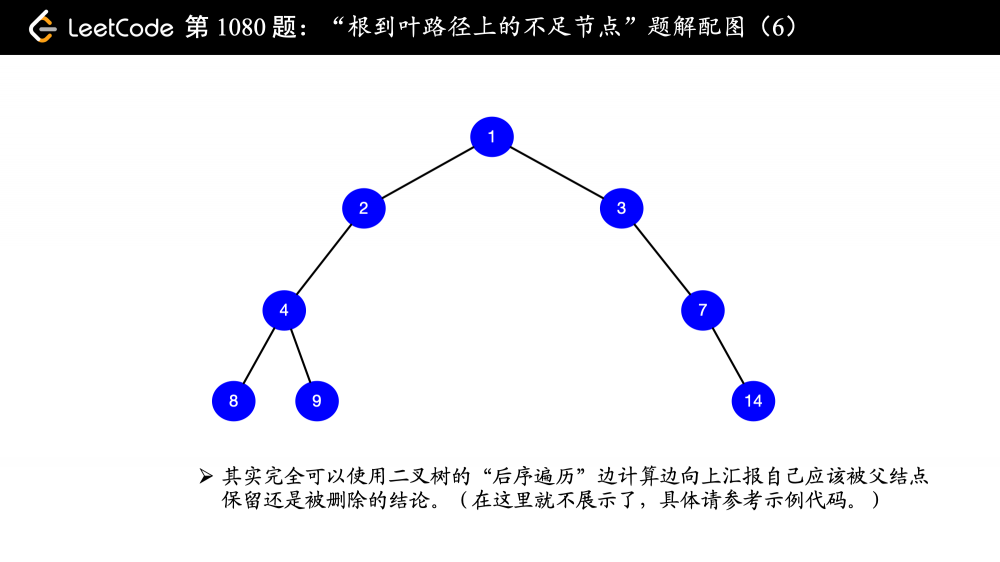
再看看我们首先考虑的问题,“告诉父亲结点,自己是否需要从二叉树中被删除”,那么 首先两个子结点(如果存在的话)要清楚自己是不是需要被删除 ,明显使用 “后序遍历”。
因此,删除结点(也可以称为 “剪枝”)的过程是从下到上的。
最后编码实现
进行后序遍历的时候,要告诉父亲节点自己是否需要从二叉树中删除,返回一个布尔值就可以了。这里编码要注意几个细节:
1、使用 Python 编码的朋友,尽量少使用 not ,否定的判断出现太多,比较容易把自己绕晕,我这一版代码是改过几次的,原先我的 __dfs 方法设置的返回值的意思是“是否保留”。后来我把返回值的含义改成“是否删除”,就是为了让逻辑中少一些 not ;
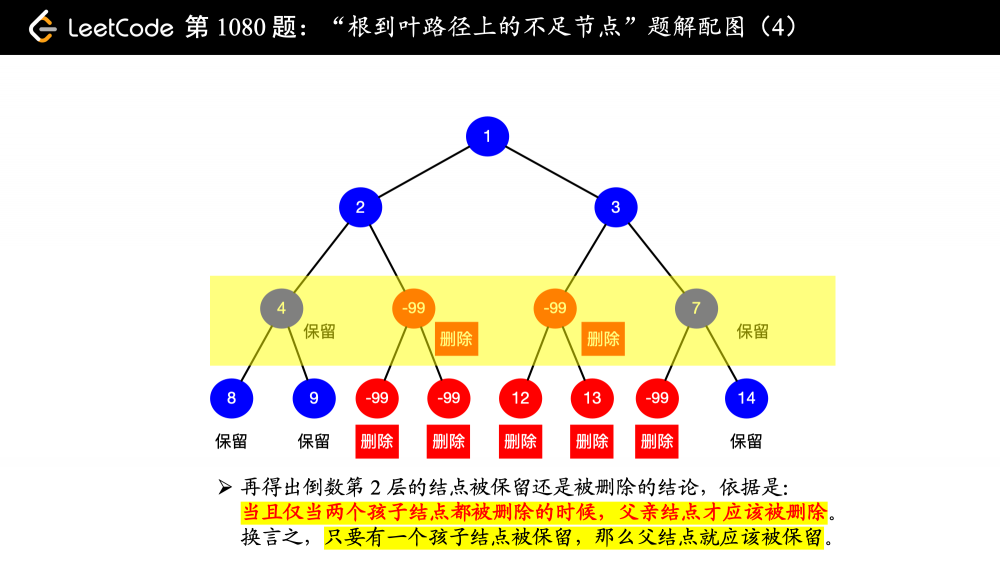
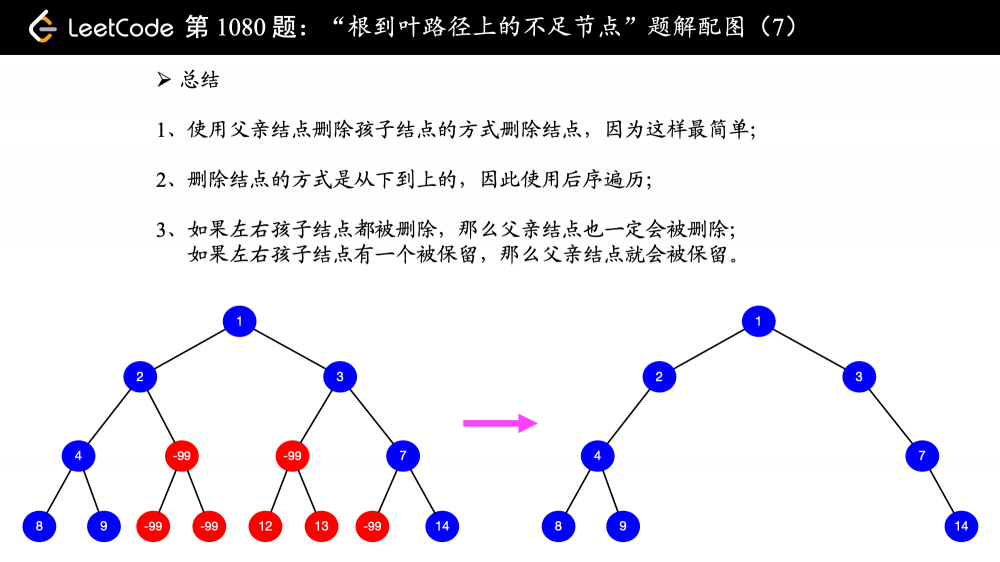
2、当一个结点不是叶子结点的时候,它是否被删除,也要看它的孩子结点, 只要孩子结点有一个被保留,父亲结点就不能被删,换句话说,父亲结点被删除当且仅当它的两个孩子结点均被删除 ;
(温馨提示:下面的幻灯片中,有几页上有较多的文字,可能需要您停留一下,可以点击右下角的后退 “|◀” 或者前进 “▶|” 按钮控制幻灯片的播放。)
 ),
),  ),
),  ),
),  ),
),  ),
),  ),
), 
3、 返回值的含义设置成“是否删除”的前提下,左右孩子的默认策略是删除,因为当只有一个孩子结点存在的时候,这个孩子结点的删除与否直接决定了父亲结点是否被删除 ,逻辑运算符 and 把不存在的那一边设置为 True ,就符合这个逻辑,不妨看看真值表,把其中一列全部设置成 True , and 的结果就正好和另外一列是一样的。
| 左子树是否被删除 | 右子树是否被删除 | and | or |
|---|---|---|---|
True |
True |
True |
True |
True |
False |
True |
False |
False |
True |
False |
True |
False |
False |
False |
False |
如果你把 __dfs 方法的返回值意义设置成 是否保留 ,你就得看 or 那一列,并且左右孩子的默认策略就是保留。
总结
这道题使用后序遍历完成,但更本质上的算法思想是分治法: 把原问题拆解成同样结构且规模更小的子问题,待子问题处理完成以后,原问题就得到了解决 ,大家想一想是不是这样。
下面展示了两种后序遍历的返回值意义的示例代码,请读者比较它们二者的差别。
如果 __dfs() 方法返回值的意义是“当前结点是否被删除”,参考代码如下。
Python 代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def __dfs(self, node, s, limit):
"""
后序遍历
:param node: 当前遍历的结点
:param s: 当前累计的和
:param limit: 题目中给出的 limit
:return: 是否要删除 node 这个结点,True 表示要删除,False 表示不删除
"""
# 先写递归终止条件:如果小于 limit,根据题意,要删除
if node.left is None and node.right is None:
return s + node.val < limit
# 默认为左右结点均剪枝,注意:初值不能设置成 False
l_tree_deleted = True
r_tree_deleted = True
# 如果有左子树,就先递归处理左子树
if node.left:
l_tree_deleted = self.__dfs(node.left, s + node.val, limit)
# 如果有右子树,就先递归处理右子树
if node.right:
r_tree_deleted = self.__dfs(node.right, s + node.val, limit)
# 左右子树是否删除的结论得到了,由自己来执行是否删除它们
if l_tree_deleted:
node.left = None
if r_tree_deleted:
node.right = None
# 只有左右子树都被删除了,自己才没有必要保留
return l_tree_deleted and r_tree_deleted
def sufficientSubset(self, root: TreeNode, limit: int) -> TreeNode:
root_deleted = self.__dfs(root, 0, limit)
if root_deleted:
return None
return root
Java 代码:
public class Solution2 {
/**
* @param node
* @param s
* @param limit
* @return 返回 node 结点是否被删除(注意:这个返回值的意义,直接影响整个逻辑。)
*/
private Boolean dfs(TreeNode node, int s, int limit) {
if (node.left == null && node.right == null) {
return s + node.val < limit;
}
// 注意:如果 dfs 的返回值的意义是这个结点是否被删除,它们的默认值应该设置为 true
boolean lTreeDeleted = true;
boolean rTreeDeleted = true;
// 如果有左子树,就先递归处理左子树
if (node.left != null) {
lTreeDeleted = dfs(node.left, s + node.val, limit);
}
// 如果有右子树,就先递归处理右子树
if (node.right != null) {
rTreeDeleted = dfs(node.right, s + node.val, limit);
}
// 左右子树是否保留的结论得到了,由自己来执行是否删除它们
if (lTreeDeleted) {
node.left = null;
}
if (rTreeDeleted) {
node.right = null;
}
// 只有左右子树都被删除了,自己才没有必要保留
return lTreeDeleted && rTreeDeleted;
}
public TreeNode sufficientSubset(TreeNode root, int limit) {
boolean rootDeleted = dfs(root, 0, limit);
if (rootDeleted) {
return null;
}
return root;
}
}
如果 __dfs() 方法返回值的意义是“当前结点是否被保留”,参考代码如下。
Python 代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
# 算法思想:分治法
# 后序遍历:dfs 的返回值是:是否保留这个节点
class Solution:
def __dfs(self, node, s, limit):
"""
后序遍历
:param node: 当前遍历的结点
:param s: 当前累计的和
:param limit: 题目中给出的 limit
:return: 是否要保留 node 这个结点,True 表示要保留,False 表示不保留
"""
# 先写递归终止条件:如果大于等于 limit,根据题意,要保留
if node.left is None and node.right is None:
return node.val + s >= limit
# 默认为左右结点均剪枝
# 注意:初值不能设置成 True
# 因为,当左右子树只有一个存在的时候,这个子树的逻辑值直接决定了父结点是否被保留
ltree_saved = False
rtree_saved = False
# 如果有左子树,就先递归处理左子树
if node.left:
ltree_saved = self.__dfs(node.left, s + node.val, limit)
# 如果有右子树,就先递归处理右子树
if node.right:
rtree_saved = self.__dfs(node.right, s + node.val, limit)
# 左右子树是否保留的结论得到了,由自己来执行是否保留它们
if not ltree_saved:
node.left = None
if not rtree_saved:
node.right = None
# 只要左右结点有一个被保留,这个结点就得被保留
return ltree_saved or rtree_saved
def sufficientSubset(self, root: TreeNode, limit: int) -> TreeNode:
root_saved = self.__dfs(root, 0, limit)
if not root_saved:
return None
return root
Java 代码:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public class Solution {
/**
* @param node
* @param s
* @param limit
* @return 返回 node 结点是否被保留(注意:这个返回值的意义,直接影响整个逻辑。)
*/
private Boolean dfs(TreeNode node, int s, int limit) {
if (node.left == null && node.right == null) {
return s + node.val >= limit;
}
// 注意:如果 dfs 的返回值的意义是这个结点是否被保留,它们的默认值应该设置为 false
boolean ltree_saved = false;
boolean rtree_saved = false;
// 如果有左子树,就先递归处理左子树
if (node.left != null) {
ltree_saved = dfs(node.left, s + node.val, limit);
}
// 如果有右子树,就先递归处理右子树
if (node.right != null) {
rtree_saved = dfs(node.right, s + node.val, limit);
}
// 左右子树是否保留的结论得到了,由自己来执行是否删除它们
if (!ltree_saved) {
node.left = null;
}
if (!rtree_saved) {
node.right = null;
}
// 左右子树有一颗被保留,自己就应该被保留
return ltree_saved || rtree_saved;
}
public TreeNode sufficientSubset(TreeNode root, int limit) {
boolean root_saved = dfs(root, 0, limit);
if (!root_saved) {
return null;
}
return root;
}
}
复杂度分析:
- 时间复杂度:$O(N)$,$N$ 为二叉树结点的个数。
- 空间复杂度:$O(1)$。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

