转载

「力扣」第 53 题：最大子序和（中等）

提示：经典的「动态规划」问题，一定要掌握。

动态规划告诉我们可以不用直接去解决题目，而是去发现这个问题最开始的样子，通过「状态」转移，每一步参考了之前计算的结果，得到最终的答案。

链接
题解链接

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例：

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶：

如果你已经实现复杂度为 $O(n)$ 的解法，尝试使用更为精妙的分治法求解。

方法一：暴力解法

即穷举所有子区间。思路虽然简单，但是写好暴力解法也不是一件容易的事情。

使用双层循环，穷举所有的子区间；
然后再对子区间内的所有元素求和；
时间复杂度是立方级别的。

参考代码 1：

这里要注意一些边界条件：

变量 i 表示结尾的那个索引；
变量 j 表示从下标 0 依次向前走。

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= i; j++) {
                int sum = sumOfSubArray(nums, j, i);
                res = Math.max(res, sum);
            }
        }
        return res;
    }

    private int sumOfSubArray(int[] nums, int left, int right) {
        // 子区间的和
        int res = 0;
        for (int i = left; i <= right; i++) {
            res += nums[i];
        }
        return res;
    }

}

C++ 代码：

#include <iostream>
#include <vector>

using namespace std;

class Solution {

private:
    int sumOfArray(vector<int> &nums, int left, int right) {
        int res = 0;
        for (int i = left; i <= right; ++i) {
            res += nums[i];
        }
        return res;
    }

public:
    int maxSubArray(vector<int> &nums) {
        int size = nums.size();
        int res = INT_MIN;
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j <= i; ++j) {
                int sum = sumOfArray(nums, j, i);
                res = max(res, sum);
            }
        }
        return res;
    }
};

复杂度分析：

时间复杂度：$O(N^3)$，这里 $N$ 为数组的长度。
空间复杂度：$O(1)$。

提交以后发现「超时」。「超时」有两种情况：

程序当中写了「死循环」；
代码正确，复杂度较高，本解法属于这种情况。

优化：事实上，上面的代码有一些重复计算。这是因为相同前缀的区间求和，可以通过类似「状态转移」的方法得到。

例如：计算子区间 [1, 4] 的和可以在计算子区间 [1, 3] 的基础上，再加上 nums[4] 得到。（这里感谢用户@YYM 的提醒）。因此，只需要枚举子序的左端点，然后再扫描右端点，就可以减少一个级别的复杂度。

参考代码 2：

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int res = Integer.MIN_VALUE;
        for (int i = 0; i < len; i++) {
            int sum = 0;
            for (int j = i; j < len; j++) {
                sum += nums[j];
                res = Math.max(res, sum);
            }
        }
        return res;
    }
}

C++ 代码：

#include <iostream>
#include <vector>


using namespace std;


class Solution {
public:
    int maxSubArray(vector<int> &nums) {
        int size = nums.size();
        int res = INT32_MIN;
        for (int i = 0; i < size; ++i) {
            int sum = 0;
            for (int j = i; j < size; ++j) {
                sum += nums[j];
                res = max(res, sum);
            }

        }
        return res;
    }
};

复杂度分析：

时间复杂度：$O(N^2)$。
空间复杂度：$O(1)$。

其实这道题是一个非常经典的动态规划问题。

该问题最早于 1977 年提出，但是直到 1984 年才被 Jay Kadane 发现了线性时间的最优解法。

方法二：动态规划

第 1 步：定义状态

既然一个连续子数组一定要以一个数作为结尾，那么我们就将状态定义成如下。

dp[i] ： 表示以 nums[i] 结尾的连续子数组的最大和 。

那么为什么这么定义呢？这是因为这样定义，状态转移方程容易得到；
怎么想到这么定义的呢？凭经验，以前做过类似问题，例如「力扣」第 300 题：最长上升子序列，或者说是凭感觉。这两道题都是动态规划的经典问题，当做例题来学习未尝不可，我学习动态规划的时候，就是直接看别人的博客和题解的。

第 2 步：思考状态转移方程

根据状态的定义，由于 nums[i] 一定会被选取，并且 dp[i] 所表示的连续子序列与 dp[i - 1] 所表示的连续子序列（有可能）就差一个 nums[i] 。

假设数组 nums 全是正数，那么一定有 dp[i] = dp[i - 1] + nums[i] 。

在一般情况下 dp[i - 1] 有可能是负数，例如前几个数都是负数，突然来了一个正数。

于是分类讨论：

如果 dp[i - 1] >= 0 ，那么可以把 nums[i] 直接接在 dp[i - 1] 表示的那个数组的后面。
如果 dp[i - 1] < 0 ，那么加上前面的数反而越来越小了，于是“另起炉灶”，单独的一个 nums[i] ，就是 dp[i] 。

以上两种情况的最大值就是 dp[i] 的值，写出如下状态转移方程：

dp[i] =

/begin{cases}

dp[i - 1] + nums[i], & if /quad dp[i - 1] /ge 0 /

nums[i], & if /quad dp[i - 1] < 0

/end{cases}

记为「状态转移方程 1」。

状态转移方程还可以这样写，反正求的是最大值，也不用分类讨论了，就这两种情况，取最大即可，因此还可以写出状态转移方程如下：

dp[i] = /max {nums[i],; dp[i - 1] + nums[i]}

记为「状态转移方程 2」。

动态规划的问题经常要分类讨论，这是因为动态规划的问题本来就有最优子结构的特征，即大问题的最优解通常由小问题的最优解得到，那么我们就需要通过分类讨论，得到大问题的小问题究竟是哪些。

第 3 步：思考初始值

dp[0] 根据定义，一定以 nums[0] 结尾，因此 dp[0] = nums[0] 。

第 4 步：思考输出

注意：这里状态的定义不是题目中的问题的定义，不能直接将最后一个状态返回回去。

输出应该是把所有的 dp[0] 、 dp[1] 、……、 dp[n - 1] 都看一遍，取最大值。同样的情况也适用于「力扣」第 300 题：最长上升子序列。我经常在这一步「摔跟头」。

参考代码 3：根据「状态转移方程 1」

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        int[] dp = new int[len];
        dp[0] = nums[0];

        for (int i = 1; i < len; i++) {
            if (dp[i - 1] >= 0) {
                dp[i] = dp[i - 1] + nums[i];
            } else {
                dp[i] = nums[i];
            }
        }

        // 最后不要忘记全部看一遍求最大值
        int res = dp[0];
        for (int i = 1; i < len; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }

}

Python 代码：

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:
            return 0
        dp = [0 for _ in range(size)]

        dp[0] = nums[0]
        for i in range(1, size):
            if dp[i - 1] >= 0:
                dp[i] = dp[i - 1] + nums[i]
            else:
                dp[i] = nums[i]
        return max(dp)

参考代码 4：根据「状态转移方程 2」

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        int[] dp = new int[len];
        dp[0] = nums[0];

        for (int i = 1; i < len; i++) {
            dp[i] = Math.max(nums[i], dp[i - 1] + nums[i]);
        }

        int res = dp[0];
        for (int i = 1; i < len; i++) {
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

Python 代码：

from typing import List


class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:
            return 0
        dp = [0 for _ in range(size)]

        dp[0] = nums[0]
        for i in range(1, size):
            dp[i] = max(dp[i - 1] + nums[i], nums[i])
        return max(dp)

复杂度分析：

时间复杂度：$O(N)$。
空间复杂度：$O(N)$。

第 5 步：思考节约空间

既然当前状态只与上一个状态有关，我们可以将空间复杂度压缩到 $O(1)$。

参考代码 5：

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        // pre 表示的意思是「上一个状态」的值
        int pre = nums[0];
        int res = pre;
        for (int i = 1; i < len; i++) {
            pre = Math.max(nums[i], pre + nums[i]);
            res = Math.max(res, pre);
        }
        return res;
    }

}

Python 代码：

from typing import List


class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:
            return 0
        # // pre 表示的意思是「上一个状态」的值
        pre = nums[0]
        res = pre
        for i in range(1, size):
            pre = max(nums[i], pre + nums[i])
            res = max(res, pre)
        return res

C++ 代码：

#include <iostream>
#include <vector>

using namespace std;

class Solution {
public:
    int maxSubArray(vector<int> &nums) {
        int res = INT_MIN;
        int pre = 0;
        for (int i = 0; i < nums.size(); ++i) {
            int cur = max(pre, 0) + nums[i];
            res = max(res, cur);
            pre = cur;
        }
        return res;
    }
};

复杂度分析：

时间复杂度：$O(N)$。
空间复杂度：$O(1)$。

方法三：分治法

分治法的思路是这样的，其实也是分类讨论。

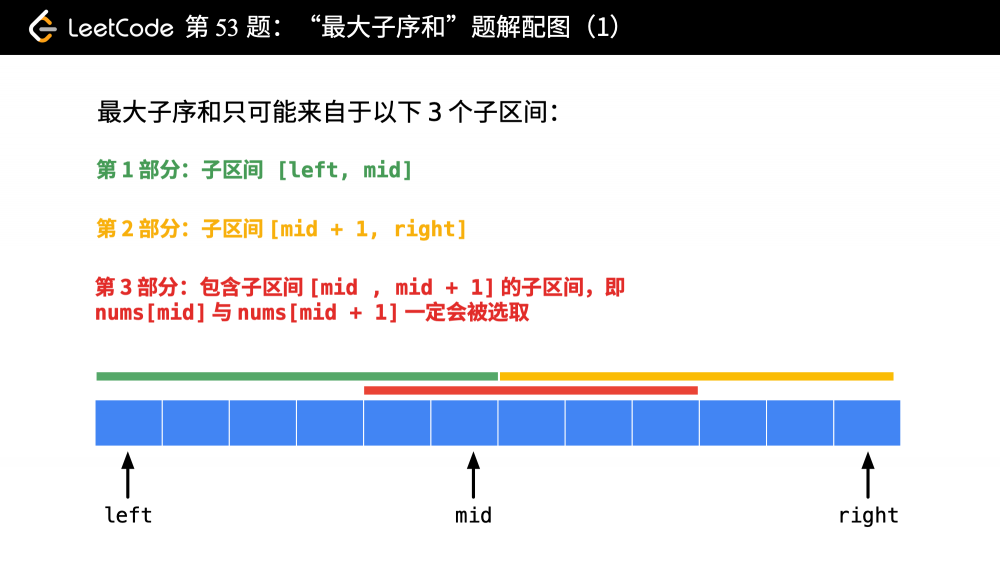
连续子序列的最大和主要由这三部分子区间里元素的最大和得到：

第 1 部分：子区间 [left, mid] ；
第 2 部分：子区间 [mid + 1, right] ；
第 3 部分：包含子区间 [mid , mid + 1] 的子区间，即 nums[mid] 与 nums[mid + 1] 一定会被选取。

对它们三者求最大值即可。

「力扣」第 53 题：最大子序和（中等）

参考代码 6：

Java 代码：

public class Solution {

    public int maxSubArray(int[] nums) {
        int len = nums.length;
        if (len == 0) {
            return 0;
        }
        return maxSubArraySum(nums, 0, len - 1);
    }

    private int maxCrossingSum(int[] nums, int left, int mid, int right) {
        // 一定会包含 nums[mid] 这个元素
        int sum = 0;
        int leftSum = Integer.MIN_VALUE;
        // 左半边包含 nums[mid] 元素，最多可以到什么地方
        // 走到最边界，看看最值是什么
        // 计算以 mid 结尾的最大的子数组的和
        for (int i = mid; i >= left; i--) {
            sum += nums[i];
            if (sum > leftSum) {
                leftSum = sum;
            }
        }
        sum = 0;
        int rightSum = Integer.MIN_VALUE;
        // 右半边不包含 nums[mid] 元素，最多可以到什么地方
        // 计算以 mid+1 开始的最大的子数组的和
        for (int i = mid + 1; i <= right; i++) {
            sum += nums[i];
            if (sum > rightSum) {
                rightSum = sum;
            }
        }
        return leftSum + rightSum;
    }

    private int maxSubArraySum(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }
        int mid = (left + right) >>> 1;
        return max3(maxSubArraySum(nums, left, mid),
                maxSubArraySum(nums, mid + 1, right),
                maxCrossingSum(nums, left, mid, right));
    }

    private int max3(int num1, int num2, int num3) {
        return Math.max(num1, Math.max(num2, num3));
    }
}

Python 代码：

from typing import List


class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        if size == 0:
            return 0
        return self.__max_sub_array(nums, 0, size - 1)

    def __max_sub_array(self, nums, left, right):
        if left == right:
            return nums[left]
        mid = (left + right) >> 1
        return max(self.__max_sub_array(nums, left, mid),
                   self.__max_sub_array(nums, mid + 1, right),
                   self.__max_cross_array(nums, left, mid, right))

    def __max_cross_array(self, nums, left, mid, right):
        # 一定包含 nums[mid] 元素的最大连续子数组的和，
        # 思路是看看左边"扩散到底"，得到一个最大数，右边"扩散到底"得到一个最大数
        # 然后再加上中间数
        left_sum_max = 0
        start_left = mid - 1
        s1 = 0
        while start_left >= left:
            s1 += nums[start_left]
            left_sum_max = max(left_sum_max, s1)
            start_left -= 1

        right_sum_max = 0
        start_right = mid + 1
        s2 = 0
        while start_right <= right:
            s2 += nums[start_right]
            right_sum_max = max(right_sum_max, s2)
            start_right += 1
        return left_sum_max + nums[mid] + right_sum_max