转载

经典柏林噪声

本文所述的柏林噪声指柏林于 1985 年提出， 2002 年改进的基于立方体晶格的以梯度作为插值因子的单噪声

本文力求在现有文献及资料的基础上，作一些补充说明，以帮助读者解答一些困惑之处。行文结构上以柏林噪声的一些基本概念为脉络，分节阐述，连贯性上可能有所欠缺，建议读者与其他资料交叉阅读。文章疏漏之处，请不吝指正！感谢！

单噪声

单噪声区别于复合噪声，柏林噪声与 Simplex 噪声、值噪声、Worley 噪声等噪声一起，作为基础噪声，来得到复杂的复合噪声。

柏林噪声函数

柏林噪声的核心是一个柏林噪声函数，该函数以坐标向量为输入参数，得到一个值域为 [-1,1] 的标量随机值。

value = noise(x,y,z)

给出空间坐标 (x,y,z) ， noise 函数将返回随机值 value 。

注：各个维度均可使用柏林噪声，柏林给出的实现为三维空间版本。以下若非特殊说明，默认为三维空间下的表述。

柏林提出理想的噪声应具有如下特性：

对旋转具有统计不变性；
能量在频谱上集中于一个窄带，即：图像是连续的，高频分量受限；
对变换具有统计不变性。

柏林噪声分布符合上述三个特性，同时，函数 符合伪随机的特性 ，即给出的坐标不变，则函数的返回值不变。

下面介绍实现柏林噪声函数所涉及的概念。

晶格

柏林噪声将空间划分为一个个单位立方体晶格，晶格以相邻的整数坐标点为顶点。若将空间原点看作是某个墙角，那么晶格就是一个一个紧靠墙角码在一起，长宽高都是一个单位的箱子。

如果将晶格的顶点代入柏林噪声函数，将得到固定的噪声值 0

noise(1, 2, 3) = 0

坐标 (1,2,3) 处的噪声值为 0.

为方便解释，以二维空间为例，假设将噪声值作为地形高度，则柏林噪声的分布以海平面为基础高度，每个网格（二维空间下晶格退化为单位正方形网格）的顶点所对应的地形高度均为零，即正好在海平面上。网格内部的地形高度在海平面附近平滑变化。

图一500*500 像素平面下，将噪声值映射至 [0-255] 的灰度值

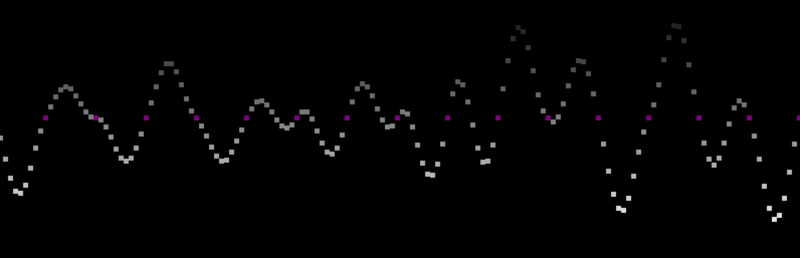
经典柏林噪声

在一维情况下，柏林噪声分布中的每一个波其波长均固定为1。

图二横轴为一维空间上点的坐标，噪声值映射至纵轴，红点为整数点的噪声值

经典柏林噪声

梯度和距离向量

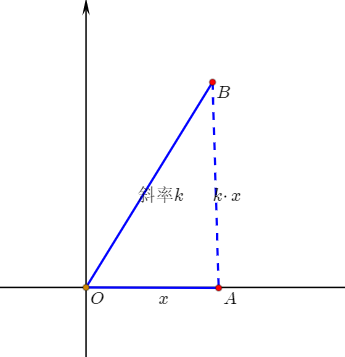
晶格顶点的噪声值已经确定了，那么晶格内部点的值如何确定呢？我们先考虑一维的情况，以一维空间的位置为 X 轴，噪声值为 Y 轴。设晶格顶点 O 位于坐标原点，OA 的距离为 x (0 < x < 1)，噪声值随 X 轴线性变化，其斜率为 k ，则易得晶格内部的点 A 对应的噪声值 y = k * x 。

图三A 点处的噪声值

经典柏林噪声

从上面的例子中，可以看到，如果噪声值线性变化，那么知道晶格顶点的斜率和点到晶格顶点的距离，即可求出给定点的噪声值。推广到高维，晶格内部点的噪声值即晶格顶点的梯度 Grade 与点到晶格顶点的距离向量 Dist 的数量积

value = Grade · Dist

以三维空间为例，若晶格顶点 O 处梯度为 Grade ，对晶格内点 A，相对于顶点 O 的距离向量 Dist ，则上述数量积 value ，即为顶点 O 在 OA 方向上的斜率与 OA 的乘积，与一维情况一致。

梯度的生成

柏林通过一个预先生成的 置换表 p 来生成梯度值。p 是一个大小为 512 的数组，数组中的每个元素都是取自 [0,255] 的随机数，对于晶格顶点 (X,Y,Z) ，有

rand = p[p[p[X]+Y]+Z]

rand 为根据顶点坐标求得的随机数，易知传入相同的坐标，将得到同样的 rand 值。

柏林建议梯度值直接从以下 12 个向量中选择，在不降低生成的噪声质量的前提下简化计算。

(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0),
(1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1),
(0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)

若将上述 12 个向量补全至 16 个向量，即可通过 rand 值的低 4 位作为索引值，索引得到确定的梯度值。

例如在 rand = 240 = 0xF0 时，其低 4 位的值为 0 ，则取得第一个梯度值 (1,1,0) 。

以上是柏林论文中的做法，读者如果有自己的伪随机数生成方式，或者有自己偏好的梯度值，也可以有自己的实现。

插值

对于给定晶格内部点来说，其相邻的晶格顶点有多个（N 维 2^(N+1) 个）。每个顶点都有自己的梯度，相对于其中任一顶点，都可以求出一个噪声值，该使用哪个呢？

如果都想用，怎么处理？可以通过插值取平均。

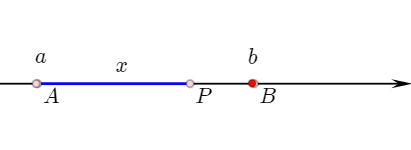
还是以一维的情况为例，设相邻晶格顶点 A 、 B 及晶格内部点 P，P 相对于 A 的噪声值为 a，P 相对于 B 的噪声值为 b， AP = x (0 < x < 1)，AB = 1，则线性插值后的噪声值为

value = lerp(a,b,x) = a*(1-x) + b*x

lerp 为线性插值函数，根据 插值系数 x 在 a 与 b 之间取值。当 x = 0 时函数值为 a，当 x = 1 时函数值为 b。

图四一维空间下 P 相对于两个相邻定点的噪声值 a，b

经典柏林噪声

对于多维的情况，通过依次做插值不断降维的方式，获得最终噪声值。

图五二维空间下 P 相对于四个相邻顶点的噪声值 a1，a2，a3，a4

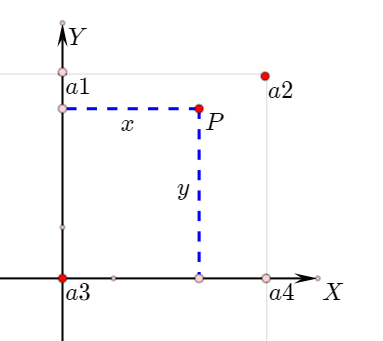
经典柏林噪声

上图中，二维网格内部点 P( x,y ) 相对于网格顶点的噪声值分别为 a1，a2，a3，a4 ，先沿 X 轴对噪声值做插值得到

b1 = lerp(a1,a2,x)
b2 = lerp(a3,a4,x)

再沿 Y 轴对噪声值 b1，b2 做插值得到

c = lerp(b1,b2,y)

c 即为最终的噪声值。即

c = noise(x,y)

noise 为二维空间下的柏林噪声函数

注：读者朋友如果玩过《2048》相信对这个插值过程会有更直观的感受。

平滑

上一节采用线性插值的方式来得到噪声值。这样得到的噪声分布比较生硬，柏林建议使用缓动函数

fade(t) = 6*t^5-15*t^4+10*t^3

对插值系数做预处理，原本的插值为

value = lerp(a,b,x)

加入平滑后为

u = fade(x)
value = lerp(a,b,u)

其他

参考链接

维基百科-柏林噪声
perlinnoise 介绍地比较细致，给出了 C# 实现
【图形学】谈谈噪声冯乐乐写的一篇关于噪声的博客，其中提到了柏林噪声

参考文献

Ken Perlin. 1985. An image synthesizer. SIGGRAPH Comput. Graph. 19, 3 (Jul. 1985), 287–296. DOI: https://doi.org/10.1145/32516...
Ken Perlin. 2002. Improving noise. ACM Trans. Graph. 21, 3 (July 2002), 681–682. DOI: https://doi.org/10.1145/56665...

代码附录

肯·柏林 2002论文 Java 版本

// https://mrl.nyu.edu/~perlin/noise/
// JAVA REFERENCE IMPLEMENTATION OF IMPROVED NOISE - COPYRIGHT 2002 KEN PERLIN.

public final class ImprovedNoise {
   static public double noise(double x, double y, double z) {
      int X = (int)Math.floor(x) & 255,                  // FIND UNIT CUBE THAT
          Y = (int)Math.floor(y) & 255,                  // CONTAINS POINT.
          Z = (int)Math.floor(z) & 255;
      x -= Math.floor(x);                                // FIND RELATIVE X,Y,Z
      y -= Math.floor(y);                                // OF POINT IN CUBE.
      z -= Math.floor(z);
      double u = fade(x),                                // COMPUTE FADE CURVES
             v = fade(y),                                // FOR EACH OF X,Y,Z.
             w = fade(z);
      int A = p[X  ]+Y, AA = p[A]+Z, AB = p[A+1]+Z,      // HASH COORDINATES OF
          B = p[X+1]+Y, BA = p[B]+Z, BB = p[B+1]+Z;      // THE 8 CUBE CORNERS,

      return lerp(w, lerp(v, lerp(u, grad(p[AA  ], x  , y  , z   ),  // AND ADD
                                     grad(p[BA  ], x-1, y  , z   )), // BLENDED
                             lerp(u, grad(p[AB  ], x  , y-1, z   ),  // RESULTS
                                     grad(p[BB  ], x-1, y-1, z   ))),// FROM  8
                     lerp(v, lerp(u, grad(p[AA+1], x  , y  , z-1 ),  // CORNERS
                                     grad(p[BA+1], x-1, y  , z-1 )), // OF CUBE
                             lerp(u, grad(p[AB+1], x  , y-1, z-1 ),
                                     grad(p[BB+1], x-1, y-1, z-1 ))));
   }
   static double fade(double t) { return t * t * t * (t * (t * 6 - 15) + 10); }
   static double lerp(double t, double a, double b) { return a + t * (b - a); }
   static double grad(int hash, double x, double y, double z) {
      int h = hash & 15;                      // CONVERT LO 4 BITS OF HASH CODE
      double u = h<8 ? x : y,                 // INTO 12 GRADIENT DIRECTIONS.
             v = h<4 ? y : h==12||h==14 ? x : z;
      return ((h&1) == 0 ? u : -u) + ((h&2) == 0 ? v : -v);
   }
   static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
   131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
   190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
   88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
   77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
   102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
   135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
   5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
   223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
   129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
   251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
   49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
   138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
   };
   static { for (int i=0; i < 256 ; i++) p[256+i] = p[i] = permutation[i]; }
}

flafla2 C# 版本

//https://gist.github.com/Flafla2/f0260a861be0ebdeef76
public class Perlin {

    public int repeat;
    
    public Perlin(int repeat = -1) {
        this.repeat = repeat;
    }

    public double OctavePerlin(double x, double y, double z, int octaves, double persistence) {
        double total = 0;
        double frequency = 1;
        double amplitude = 1;
        double maxValue = 0;            // Used for normalizing result to 0.0 - 1.0
        for(int i=0;i<octaves;i++) {
            total += perlin(x * frequency, y * frequency, z * frequency) * amplitude;
            
            maxValue += amplitude;
            
            amplitude *= persistence;
            frequency *= 2;
        }
        
        return total/maxValue;
    }
    
    private static readonly int[] permutation = { 151,160,137,91,90,15,                    // Hash lookup table as defined by Ken Perlin.  This is a randomly
        131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,    // arranged array of all numbers from 0-255 inclusive.
        190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
        88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
        77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
        102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
        135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
        5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
        223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
        129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
        251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
        49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
        138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
    };
    
    private static readonly int[] p;                                                     // Doubled permutation to avoid overflow
    
    static Perlin() {
        p = new int[512];
        for(int x=0;x<512;x++) {
            p[x] = permutation[x%256];
        }
    }
    
    public double perlin(double x, double y, double z) {
        if(repeat > 0) {                                    // If we have any repeat on, change the coordinates to their "local" repetitions
            x = x%repeat;
            y = y%repeat;
            z = z%repeat;
        }
        
        int xi = (int)x & 255;                                // Calculate the "unit cube" that the point asked will be located in
        int yi = (int)y & 255;                                // The left bound is ( |_x_|,|_y_|,|_z_| ) and the right bound is that
        int zi = (int)z & 255;                                // plus 1.  Next we calculate the location (from 0.0 to 1.0) in that cube.
        double xf = x-(int)x;                                // We also fade the location to smooth the result.
        double yf = y-(int)y;i
        double zf = z-(int)z;
        double u = fade(xf);
        double v = fade(yf);
        double w = fade(zf);
                                                            
        int aaa, aba, aab, abb, baa, bba, bab, bbb;
        aaa = p[p[p[    xi ]+    yi ]+    zi ];
        aba = p[p[p[    xi ]+inc(yi)]+    zi ];
        aab = p[p[p[    xi ]+    yi ]+inc(zi)];
        abb = p[p[p[    xi ]+inc(yi)]+inc(zi)];
        baa = p[p[p[inc(xi)]+    yi ]+    zi ];
        bba = p[p[p[inc(xi)]+inc(yi)]+    zi ];
        bab = p[p[p[inc(xi)]+    yi ]+inc(zi)];
        bbb = p[p[p[inc(xi)]+inc(yi)]+inc(zi)];
    
        double x1, x2, y1, y2;
        x1 = lerp(    grad (aaa, xf  , yf  , zf),                // The gradient function calculates the dot product between a pseudorandom
                    grad (baa, xf-1, yf  , zf),                // gradient vector and the vector from the input coordinate to the 8
                    u);                                        // surrounding points in its unit cube.
        x2 = lerp(    grad (aba, xf  , yf-1, zf),                // This is all then lerped together as a sort of weighted average based on the faded (u,v,w)
                    grad (bba, xf-1, yf-1, zf),                // values we made earlier.
                      u);
        y1 = lerp(x1, x2, v);

        x1 = lerp(    grad (aab, xf  , yf  , zf-1),
                    grad (bab, xf-1, yf  , zf-1),
                    u);
        x2 = lerp(    grad (abb, xf  , yf-1, zf-1),
                      grad (bbb, xf-1, yf-1, zf-1),
                      u);
        y2 = lerp (x1, x2, v);
        
        return (lerp (y1, y2, w)+1)/2;                        // For convenience we bound it to 0 - 1 (theoretical min/max before is -1 - 1)
    }
    
    public int inc(int num) {
        num++;
        if (repeat > 0) num %= repeat;
        
        return num;
    }
    
    public static double grad(int hash, double x, double y, double z) {
        int h = hash & 15;                                    // Take the hashed value and take the first 4 bits of it (15 == 0b1111)
        double u = h < 8 /* 0b1000 */ ? x : y;                // If the most significant bit (MSB) of the hash is 0 then set u = x.  Otherwise y.
        
        double v;                                            // In Ken Perlin's original implementation this was another conditional operator (?:).  I
                                                            // expanded it for readability.
        
        if(h < 4 /* 0b0100 */)                                // If the first and second significant bits are 0 set v = y
            v = y;
        else if(h == 12 /* 0b1100 */ || h == 14 /* 0b1110*/)// If the first and second significant bits are 1 set v = x
            v = x;
        else                                                 // If the first and second significant bits are not equal (0/1, 1/0) set v = z
            v = z;
        
        return ((h&1) == 0 ? u : -u)+((h&2) == 0 ? v : -v); // Use the last 2 bits to decide if u and v are positive or negative.  Then return their addition.
    }
    
    public static double fade(double t) {
                                                            // Fade function as defined by Ken Perlin.  This eases coordinate values
                                                            // so that they will "ease" towards integral values.  This ends up smoothing
                                                            // the final output.
        return t * t * t * (t * (t * 6 - 15) + 10);            // 6t^5 - 15t^4 + 10t^3
    }
    
    public static double lerp(double a, double b, double x) {
        return a + x * (b - a);
    }
}

原文 https://segmentfault.com/a/1190000022628192

正文到此结束