KMP算法思路总结
KMP算法一开始学起来要被绕晕，但事实上，只要掌握其中逻辑思路，还是很好学的。
我们设主串为S，子串为a
现在第一部分两者匹配，也就是说，S串的打钩部分与a串打钩部分是完全一样的，但是，S【i】与a【k】是不相同的。如果按照常规思路，我们只会把a串往后移一个（朴素算法的过程也可以这么理解），但这样时间上会浪费不少，如何优化呢？
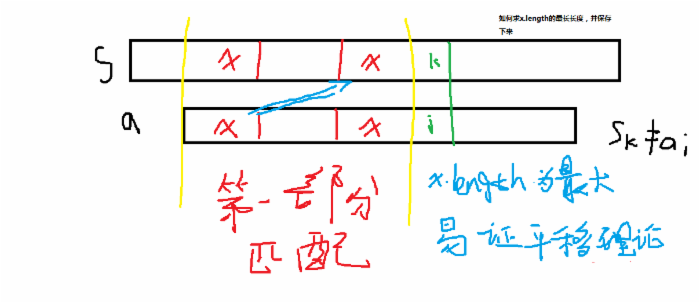
假设，在第一部分匹配区中，a串存在这样一个子串（它既在a的头部，并且又在a的尾部，且x的长度尽可能大。。。事实上是要求最大化），我们把这个子串叫做x，那么，我们可以看到，第一部分匹配中，x存在四个区域，那么，当匹配发生错误时，即S【k】！=a【i】，我们可以把a平移，这次不是平移一个单位，而是直接把a中的第一个x与s中的x对齐。这里就省下许多时间。
证明：
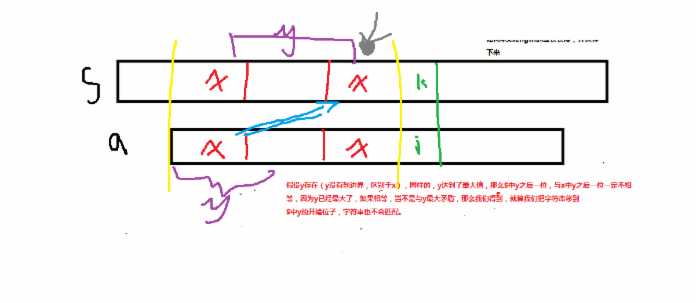
假设y存在（y没有到边界，区别于x），同样的，y达到了最大值，那么S中y之后一位，与a中y后一位一定不会相等，因为已经最大了，如果相等，岂不是与y最大矛盾，那么我们得到，就算我们把字符串移到S中y的开始位子，字符串也不会匹配。而我们又论证了x的正确性（看第二张图。。。），并且我们能选择的，也就是x，y其中之一，y既然注定是错误的，从最优化考虑，就剩下x。
接下来就是如何求x的长度问题，我们设next【】来保存x的长度（在a中），这里我们采用递推法：
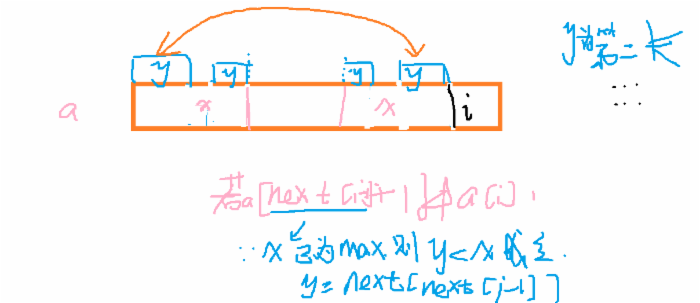
if a[next[i-1]+1=a[i】 then next[i] = next[i-1]+1
else 找到第二大的x，也就是y，递归
这里讲一下第二大的x怎么求，第二大的x满足条件是，x第二大比第一大要小，也就是在第一大x的内部。如果在x内部找到最大的y（第二大x），一定满足图示，那么y可求。
KMP算法就是这样了。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
