转载

归并排序 & 快速排序

SpongeBob's Tech Space

生活："When in doubt, use brute force." --Ken Thompson

博客园
首页
新随笔
联系
订阅
管理

随笔- 36 文章- 0 评论- 19

归并排序 & 快速排序

归并排序

归并排序是建立在归并操作上的一种有效的排序算法,该算法是 采用分治法（Divide and Conquer） 的一个非常典型的应用。

将已有序的子序列合并，得到完全有序的序列 ；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并过程为：

比较a[i]和a[j]的大小，若a[i]≤a[j]，则将第一个有序表中的元素a[i]复制到r[k]中，并令i和k分别加上1；

否则将第二个有序表中的元素a[j] 复制到r[k]中，并令j和k分别加上1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到r中从下标k到下标t的单元。

归并排序的算法我们通常用递归实现，先把待排序区间[s,t]以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间[s,t]。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

1、归并排序

Merge Sort
mergeSort.h :

#include <assert.h>  #include <stdio.h>  #include <stdlib.h>  void merge (int a[], int b[], int c[], int m, int n);  void mergesort (int key[], int n);  void wrt (int key[], int sz);

.
.
merge.c :

/* Merge a[] of size m and b[] of size n into c[]. */  #include "mergesort.h"  void merge (int a[], int b[], int c[], int m, int n)  {   int i = 0, j = 0, k = 0;   ;   while (i < m && j < n)       if (a[i] < b[j])           c[k++] = a[i++];       else           c[k++] = b[j++];   ;   while (i < m)               /* pick up any remainder */       c[k++] = a[i++];   ;   while (j < n)       c[k++] = b[j++];  }

.
.
mergesort.c :

/* Mergesort: Use merge() to sort an array of size n. */  #include "mergesort.h"  void mergesort (int key[], int n)  {   int j, k, m, *w;   for (m = 1; m < n; m *= 2)   ;                           /* m is a power of 2 */   if (n < m) {       printf("ERROR: Array size not a power of 2 - bye! /n");       exit(1);   }   w = calloc (n, sizeof(int));    /* allocate workspace */   assert(w != NULL);              /* check that calloc() worked */   for (k = 1; k < n; k *=2)   {       for (j = 0; j < n-k; j += 2*k)           /* Merge two subarrays of key[] into a subarray of w[]. */           merge(key + j, key+j+k, w+j, k, k)       for (j = 0; j < n; ++j)           key[j] = w[j];          /* write w back into key */   }   free(w);                        /* free the workspace */  }

.
.
main.c :

/* Test merge() and mergesort(). */  #include "mergesort.h"  int main(void)  {   int sz, key[] = { 4, 3, 1, 67, 55, 8, 0, 4,                     -5, 37, 7, 4, 2, 9, 1, -1                   };   sz = sizeof(key) / sizeof(int); /* the size of key[] */   printf("Before mergesort:/n");   wrt(key, sz);   mergesort(key, sz);   printf("After mergesort:/n");   wrt(key, sz);   return 0;  }

wrt.c :

#include "mergesort.h"  void wrt(int key[], int sz)  {   int i;   for (i = 0; i < sz; ++i)       printf("%4d %s", key[i], ((i < sz-1) ? " " : "/n"));  }

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

快速排序

快速排序（Quicksort）是对冒泡排序的一种改进。

基本思想：－－二分查找

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

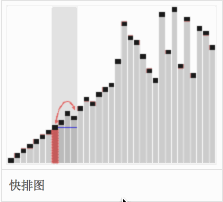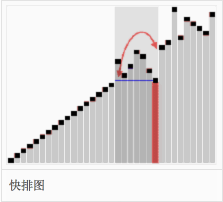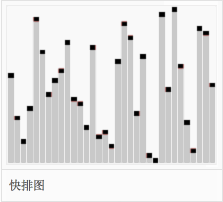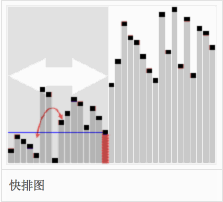归并排序 & 快速排序快速排序图

1. 设要排序的数组是A[0]……A[N-1]。首先任意选取一个数据（通常选用数组的第一个数）作为关键数据，然后将所有比它小的数都放到它前面，所有比它大的数都放到它后面，这个过程称为一趟快速排序。

2. 快速排序不是一种稳定的排序算法，也就是说，多个相同的值的相对位置也许会在算法结束时产生变动。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

2、快速排序

Quick Sort

/* Quicksort! Pointer version with macros. */  #define swap(x, y) {int t; t = x; x = y; y = t;}  #define order(x, y) if (x > y) swap(x, y)  #define o2(x, y) order(x, y)  #define o3(x, y, z) o2(x, y); o2(x, z); ow(y, z)  #typedef enum {yes, no} yes_no;  static yes_no find_pivot(int *left, int *right, int *pivot_ptr);  static int     *partition(int *left, int *right, int pivot);

.
.
.//利用“递归”实现，基本思路：“分治法” quicksort(a, a+N-1);

void quicksort(int *left, int *right)  {   int *p, pivot;   if (find_pivot(left, right, &pivot) == yes) {       p = partition(left, right, pivot);       quicksort(left, p-1);       quicksort(p, right);   }  }

static yes_no find_pivot(int *left, int *right, int *pivot_ptr)  {   int a, b, c, *p;   a = *left;                              /* left value */   b = *(left + (right - left) / 2);       /* middle value */   c = *right;   ;   o3(a, b, c);   if (a < b) {       *pivot_ptr = b;       return yes;   }   if (b < c) {       *pivot_ptr = c;       return yes;   }   ;   for (p = left+1; p <= right; ++p)       if (*p != *left) {           *pivot_ptr = (*p < *left) ? *left : *p;           return yes;       }   return no;              /* all elements have the same value */  }

.
.
.// 主要工作由partation()函数完成

static int *partation(int *left, int *right, int pivot) {  while (left <= right) {      while (*left < pivot)  ++left;      while (*right >= pivot)  --right;      if (left < right) {  swap(*left, *right);  ++left;  --right;      }  }  return left; }

.
.
ex:
使用“快速”排序，高效率，复杂度：n log n

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

PS：

递归

递归算法一般用于解决三类问题：

(1)数据的定义是按递归定义的。（ Fibonacci函数 ）

(2)问题解法按递归算法实现。

这类问题虽则本身没有明显的递归结构，但用递归求解比迭代求解更简单，如Hanoi问题。

(3)数据的结构形式是按递归定义的。

如二叉树、广义表等，由于结构本身固有的递归特性，则它们的操作可递归地描述。

递归的缺点：

递归算法解题相对常用的算法如普通循环等，运行效率较低。因此，应该尽量避免使用递归，除非没有更好的算法或者某种特定情况，递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等。

递归典型问题：梵塔问题（ 汉诺塔问题 ）

已知有三根针分别用A, B, C表示，在A中从上到下依次放n个从小到大的盘子，现要求把所有的盘子

从A针全部移到B针，移动规则是：可以使用C临时存放盘子，每次只能移动一块盘子，而且每根针上

不能出现大盘压小盘，找出移动次数最小的方案.

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

PS：

［ 每日一句 ］

There’s a plan to make all of this right.

［ 每天一首英文歌 ］

" Call me maybe " - Carly Rae Jepsen

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

|-> GitHub: SpongeBob-GitHub

posted @ 2015-05-17 11:46 Bing_Ma 阅读( ... ) 评论( ... )编辑收藏

刷新评论刷新页面返回顶部

博客园首页博问新闻闪存程序员招聘知识库

$(function() { $(window).scroll(function() { if ($(window).scrollTop() > 1000) $('div.go-top').show(); else $('div.go-top').hide(); }); $('div.go-top').click(function() { $('html, body').animate({scrollTop: 0}, 1000); }); });

正文到此结束