转载

堆排序--java实现

一.堆排序

堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于(或者大于)它的父节点。

二、堆

什么是堆？

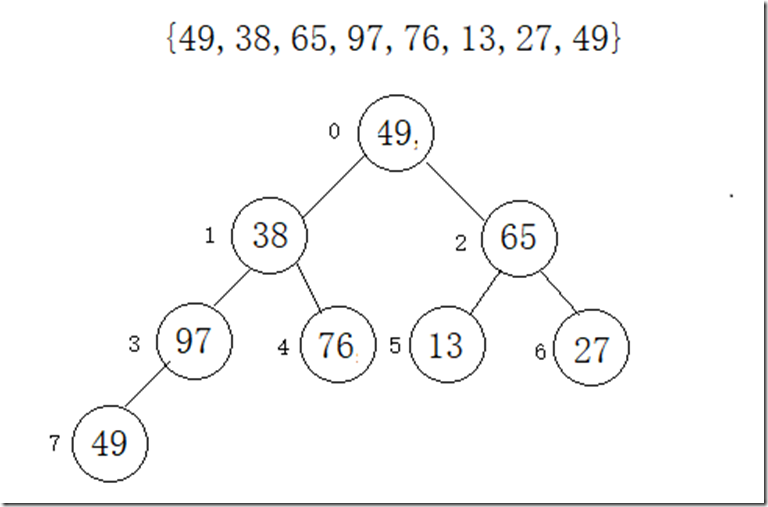
堆是一个树形结构，其实堆的底层是一棵完全二叉树。而完全二叉树是一层一层按照进入的顺序排成的。按照这个特性，我们可以用数组来按照完全二叉树实现堆。

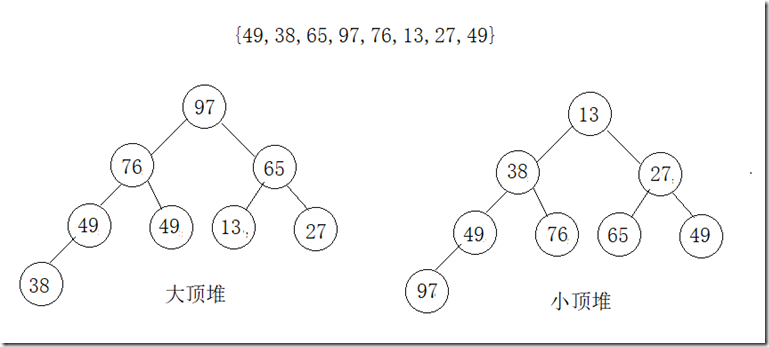
堆排序--java实现大顶堆与小顶堆

大顶堆原理：根结点（亦称为堆顶）的关键字是堆里所有结点关键字中最大者，称为大顶堆。大顶堆要求根节点的关键字既大于或等于左子树的关键字值，又大于或等于右子树的关键字值。

小顶堆原理：根结点（亦称为堆顶）的关键字是堆里所有结点关键字中最小者，称为小顶堆。小堆堆要求根节点的关键字既小于或等于左子树的关键字值，又小于或等于右子树的关键字值。

堆排序--java实现

三、推排序思想

构建初始堆，将待排序列构成一个大顶堆(或者小顶堆)，升序大顶堆，降序小顶堆；
将堆顶元素与堆尾元素交换，并断开(从待排序列中移除)堆尾元素。
重新构建堆。
重复2~3，直到待排序列中只剩下一个元素(堆顶元素)。

四、图解

堆排序--java实现

五.代码实现

public class HeapSort {

    public static void main(String[] args) {

        List<Integer> list = new ArrayList<Integer>();

        for (int i = 0; i < 10; i++) {
            list.add((int) (Math.random() * 100));
        }
        System.out.println("排序前的集合为：");
        System.out.println(Arrays.toString(list.toArray()));

        heapSort(list);

        System.out.println("排序后的集合为：");
        System.out.println(Arrays.toString(list.toArray()));
    }

    /**
     * 创建堆，
     * @param list 待排序列
     */
    private static void heapSort(List<Integer> list) {
        //创建堆
        for (int i = (list.size() - 1) / 2; i >= 0; i--) {
            //从第一个非叶子结点从下至上，从右至左调整结构
            adjustHeap(list, i, list.size());
        }

        System.out.println("dadui的集合为：");
        System.out.println(Arrays.toString(list.toArray()));

        //调整堆结构+交换堆顶元素与末尾元素
        for (int i = list.size() - 1; i > 0; i--) {
            //将堆顶元素与末尾元素进行交换
            int temp = list.get(i);
            list.set(i, list.get(0));
            list.set(0, temp);

            //重新对堆进行调整
            adjustHeap(list, 0, i);
        }
    }

    /**
     * 调整堆
     * @param list 待排序列
     * @param parent 父节点
     * @param length 待排序列尾元素索引
     */
    private static void adjustHeap(List<Integer> list, int parent, int length) {
        //将temp作为父节点
        int temp = list.get(parent);
        //左孩子
        int lChild = 2 * parent + 1;

        while (lChild < length) {
            //右孩子
            int rChild = lChild + 1;
            // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
            if (rChild < length && list.get(lChild) < list.get(rChild)) {
                lChild++;
            }

            // 如果父结点的值已经大于孩子结点的值，则直接结束
            if (temp >= list.get(lChild)) {
                break;
            }

            // 把孩子结点的值赋给父结点
            list.set(parent, list.get(lChild));

            //选取孩子结点的左孩子结点,继续向下筛选
            parent = lChild;
            lChild = 2 * lChild + 1;
        }
        list.set(parent, temp);
    }

}

原文 https://segmentfault.com/a/1190000023294930

正文到此结束