趣题：不等式背后的直观意义
有时，为了说明某个式子始终成立，我们会为它构造一个情境。例如，为了说明
C(m, 0) · C(w, r) + C(m, 1) · C(w, r – 1) + … + C(m, r) · C(w, 0) = C(m + w, r)
始终成立，只需要注意到，等号的左边和右边计算的都是同一个东西：假如一个班上有 m 个男生 w 个女生，从中选出 r 个人有多少种方案。等号左边的计算方式是，分别计算 0 男 r 女、 1 男 r – 1 女、 2 男 r – 2 女等 r + 1 种情况的方案数，然后把它们加起来。等号右边则是直接算出了从这 m + w 个人中选出 r 个人的方案数。两种算法所得的答案应该是相等的。
现在，请你构造一个情境，来说明不等式
(1 – p m ) n + (1 – q n ) m ≥ 1
总成立，其中 m 、 n 是任意正整数， p 、 q 是任意正实数，并且满足 p + q ≤ 1 。
假设有一个三角形 ABC ，其中从 B 顶点引出 n 条射线，与 AC 边交于 n 个点，又从 C 顶点引出 m 条射线，与 AB 边交于 m 个点。所有这些线条在三角形内一共产生了 mn 个交点。现在，在每一个交点处都画一个小圆，于是每个小圆内都会有两条小线段。对于每一个小圆，我们都随机从下述三个操作中选择一个来执行。
- 擦去 C 点所引射线上的小线段，仅保留 B 点所引射线上的小线段
- 擦去 B 点所引射线上的小线段，仅保留 C 点所引射线上的小线段
- 擦去圆内的全部两条小线段
三种操作各自被选中的概率分别为 p 、 q 和 1 – p – q 。于是，每一个小圆里都最多只留下了一条小线段。
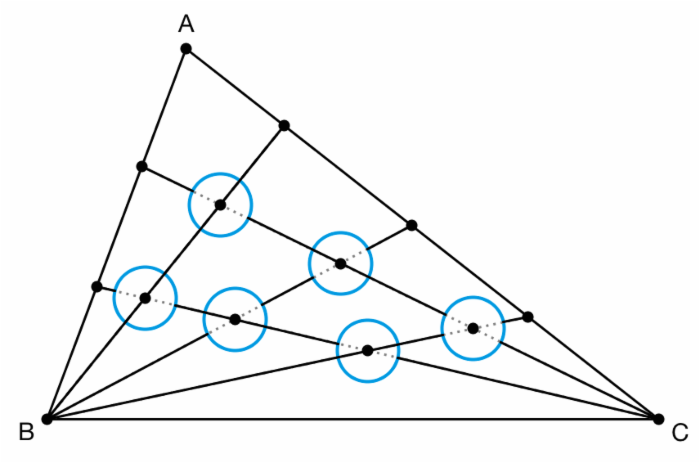
每条从 B 点出发的线上都有 m 个小圆，这条线在 m 个小圆内都被保留下来了的概率是 p m ，因而整条线有断掉之处的概率就是 1 – p m 。从 B 点出发的线一共有 n 条，每条线都有断掉之处的概率就是 (1 – p m ) n 。因此，至少有一条线完好无缺的概率就是 1 – (1 – p m ) n 。类似地，从 C 点出发的 m 条线当中，至少有一条线完好无缺的概率就是 1 – (1 – q n ) m 。
但是，从 B 点出发的线条只要有一条是完全连通的，都会使得从 C 点出发的所有线条都断掉；从 C 点出发的线条只要有一条是完全连通的，都会使得从 B 点出发的所有线条都断掉。因此，存在某条从 B 点出发的完好的线，与存在某条从 C 点出发的完好的线，这两个事件是互斥的。这说明
(1 – (1 – p m ) n ) + (1 – (1 – q n ) m ) ≤ 1
整理可得
(1 – p m ) n + (1 – q n ) m ≥ 1
这个问题来自 Ross Honsberger 的 More Mathematical Morsels 一书。
正文到此结束
热门推荐
相关文章
Loading...
![[HBLOG]公众号](http://www.liuhaihua.cn/img/qrcode_gzh.jpg)
