安全科普:详解Windows Hash与破解
概述
1.1 hash
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
常用hash算法的介绍:
(1)MD4
MD4(RFC 1320)是 MIT 的Ronald L. Rivest在 1990 年设计的,MD 是 Message Digest(消息摘要) 的缩写。它适用在32位字长的处理器上用高速软件实现——它是基于 32位操作数的位操作来实现的。
(2)MD5
MD5(RFC 1321)是 Rivest 于1991年对MD4的改进版本。它对输入仍以512位分组,其输出是4个32位字的级联,与 MD4 相同。MD5比MD4来得复杂,并且速度较之要慢一点,但更安全,在抗分析和抗差分方面表现更好。
(3)SHA-1及其他
SHA1是由NIST NSA设计为同DSA一起使用的,它对长度小于264的输入,产生长度为160bit的散列值,因此抗穷举(brute-force)性更好。SHA-1 设计时基于和MD4相同原理,并且模仿了该算法。
Hash算法在信息安全方面的应用主要体现在以下的3个方面:
(1)文件校验
我们比较熟悉的校验算法有奇偶校验和CRC校验,这2种校验并没有抗数据篡改的能力,它们一定程度上能检测并纠正数据传输中的信道误码,但却不能防止对数据的恶意破坏。
MD5 Hash算法的"数字指纹"特性,使它成为目前应用最广泛的一种文件完整性校验和(Checksum)算法,不少Unix系统有提供计算md5 checksum的命令。
(2)数字签名
Hash 算法也是现代密码体系中的一个重要组成部分。由于非对称算法的运算速度较慢,所以在数字签名协议中,单向散列函数扮演了一个重要的角色。对 Hash 值,又称"数字摘要"进行数字签名,在统计上可以认为与对文件本身进行数字签名是等效的。而且这样的协议还有其他的优点。
(3) 鉴权协议
如下的鉴权协议又被称作挑战–认证模式:在传输信道是可被侦听,但不可被篡改的情况下,这是一种简单而安全的方法。以上就是一些关于hash以及其相关的一些基本预备知识。
windows hash
Windows hash由二部分组成,分别是LM HASH&NT HASH。Windows系统关于hash的组成如下:
用户名称:RID:LM-HASH值:NT-HASH值
2.1 Windows下LM HASH生成原理
LM HASH生成规则如下:
1.用户的密码被限制为最多14个字符。 2.用户的密码转换为大写。 3.系统中用户的密码编码使用了OEM内码页 4.密码不足14字节将会用0来补全。 5.固定长度的密码被分成两个7byte部分。每部分转换成比特流,在分7bit为一组末尾加0,组成新的编码 6.上步骤得到的8byte二组,分别作为DES key为“KGS!@#$%”进行加密。 7.将二组DES加密后的编码拼接,得到最终LM HASH值。
实例演示:
· 假设明文口令是“admin”,首先全部转换成大写“ADMIN”,
· 密码字符串大写后变换成十六进制串:41444D494E
· 转换后的十六进制字符串按照二进制计算只有40bit,为了满足14字节的要求,所以需要补全72bit的二进制0,得最终补全后十六进制为:41444D494E000000000000000000
· 将上述编码(41444D494E000000000000000000)分成2组7byte的数据,分别为:
41444D494E0000
00000000000000
· 将每一组7byte的十六进制转换为二进制,每7bit一组末尾加0,在转换成十六进制组成得到2组8byte的编码:
41444D494E0000—>40A212A894700000
00000000000000—>0000000000000000
· 利用上面计算出来的2组编码,作为DES加密key分别对“KGS!@#$%”(换算成十六进制:4B47532140232425)字符,进行DES加密,如下:
40A212A894700000—-DES加密—-F0D412BD764FFE81
0000000000000000—-DES加密—-AAD3B435B51404EE
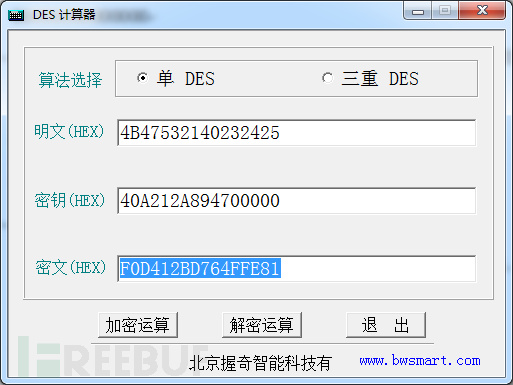
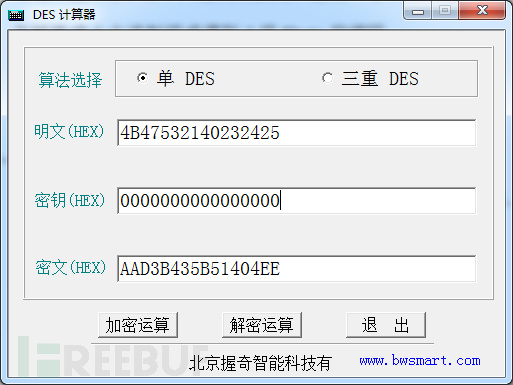
· 将二组值拼接,最终得到LM HASH值为:
F0D412BD764FFE81 AAD3B435B51404EE
验证如下图:
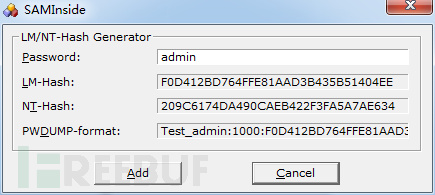
2.2 Windows下NTLM Hash生成原理
IBM设计的LM Hash算法存在几个弱点,微软在保持向后兼容性的同时提出了自己的挑战响应机制,NTLM Hash便应运而生。假设明文口令是"123456",首先转换成Unicode字符串,与LM Hash算法不同,这次不需要添加0补足14字节
"123456"->310032003300340035003600。
从ASCII串转换成Unicode串时,使用little-endian序,微软在设计整个SMB协议时就没考虑过big-endian 序,ntoh*()、hton*()函数不宜用在SMB报文解码中。0×80之前的标准ASCII码转换成Unicode码,就是简单地从0x??变成 0×00??。此类标准ASCII串按little-endian序转换成Unicode串,就是简单地在原有每个字节之后添加0×00。对所获取的 Unicode串进行标准MD4单向哈希,无论数据源有多少字节,MD4固定产生128-bit的哈希值,16字节 310032003300340035003600-进行标准MD4单向哈希->32ED87BDB5FDC5E9 CBA88547376818D4,就得到了最后的NTLM Hash
NTLM Hash:32ED87BDB5FDC5E9CBA88547376818D4。
与LM Hash算法相比,明文口令大小写敏感,无法根据NTLM Hash判断原始明文口令是否小于8字节,摆脱了魔术字符串"KGS!@#$%"。MD4是真正的单向哈希函数,穷举作为数据源出现的明文,难度较大。
验证如下:

开始破解
3.1 抓取windows hash
在windows中分别用了LM HASH和NTLM HASH对密码进行了加密,所以抓取任意一个HASH都可以破解密码,只不过如果二个HASH都可以抓到,密码的破译成功率会大大提升。经常使用抓windows hash的工具很多,像SAMInside,gethash等等。个人比较倾向于使用SAMinside工具,该工具不仅可以在线抓取windows hash 还可以导入存储windows hash的 sam等文件获取hash值。
文件位置:
C:/windows/system32/config/SAM
在windows xp,server2003之前包括xp&2003的系统都可以通过工具抓取到完整的LM HASH&NT HASH的。这样就可以直接通过在线的破译网站进行密码破解。
但是之后的系统可以改变一些设置让操作系统存储LM HASH值到SAM文件中。方便我们的抓取。
3.1.1 xp下hash抓取及破解(略)
3.1.2 win 7下hash抓取及破解
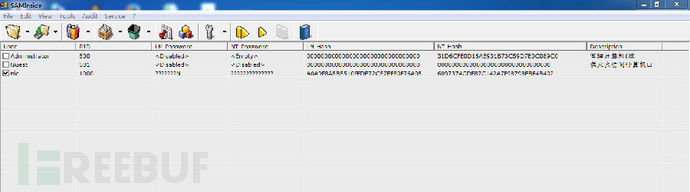
步骤一:导入本地的用户hash值
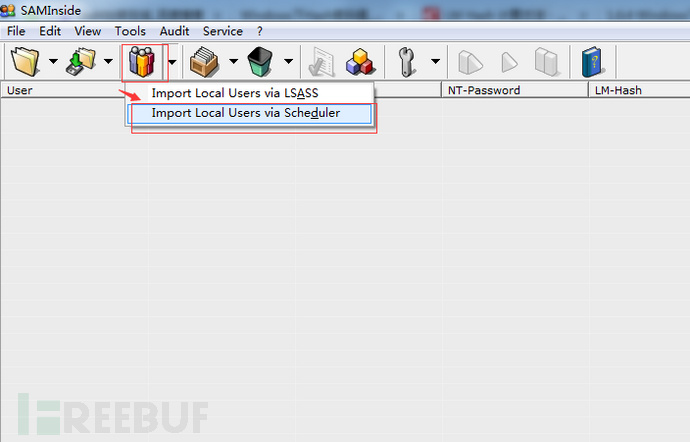
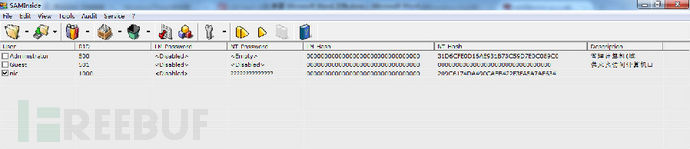
看不清图片,用户名为nic的NT HASH为:209C6174DA490CAEB422F3FA5A7AE634
可以看到只能抓取到NT HASH值,我们也可以通过NT HASH去破解windows密码的,因为LM HASH和NT HASH只是二种不同的加密方式,针对同一个密码。
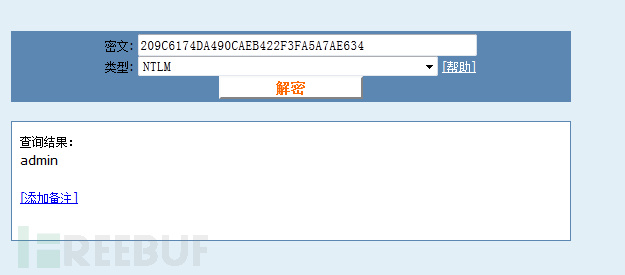
看到了吧,没有LM HASH照样可以破密码的哟。只是有了LM HASH破解成功率会多点。
但是当通过NT HASH无法破译密码的时候,我们就要想办法把LM HASH给搞出来,通过更改本地安全策略设置,具体步骤如下:
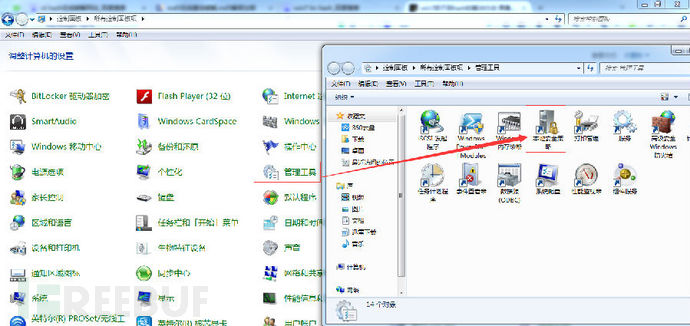

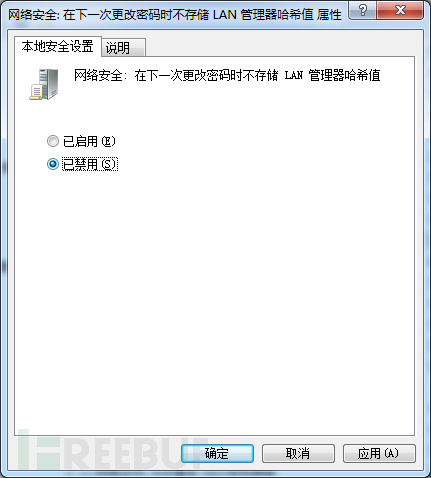
但是这个法子有点局限就是,必须下一次更改密码后才生效。唉~
改完密码后再抓:
LMHASH:A0A9F8A5B5510FFDE72C57EF50F76A05
NT HASH: 6097374CDF87C142A7F98798EBF4B402
我们先针对每一个生成的HASH进行破解:
LM HASH破解:
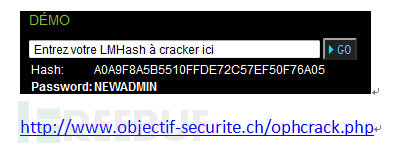
只有LM,破解出来的是大写,我的是小写的。不知道是那里的问题。
NT HASH破解:(ps: 换个长一点的密码就付费了)
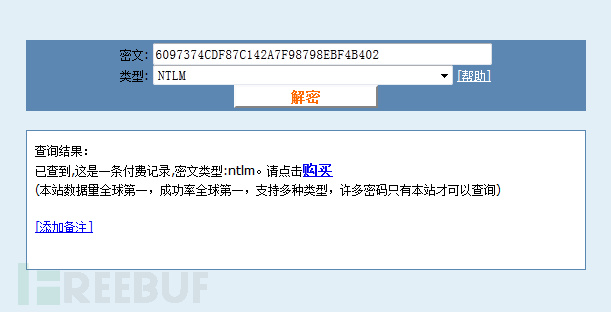
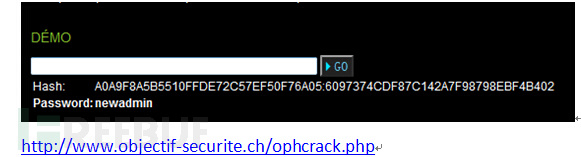
双剑合璧,LM HASH&NT HASH破解:
输入格式, LM HASH:NT HASH,正确密码就出来了










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

