改进反向传播算法估计量的有界性
（翻译自文章《Boundedness of Estimator with an Improved Back Propagation Algorithm》关键章节）
本文提出了一个新颖的学习算法，一个多层次神经网络中一个变量学习增益和一个a修正术语。这个学习增益通过LM算法决定，LM算法是一个非线性最小二乘方法。数据大小和学习速率之间关系被考虑和一个鲁棒的自适应控制理论观点显示权重的有界性。此外，简单的数值模拟表明提出学习算法的效率。
- 1、介绍
多层神经网络所使用的作用之一是近似一个未知有界非线性函数。神经网络中基本的学
习算法是反向传播算法。这个算法是基于梯度下降方法，所以权重的有界性没有保证。此外，学习增益很难决定，因为一个大的学习增益往往导致权重发散，一个小的学习增益导致学习速度慢。
为了避免这些困难，提出了改进的反向传播算法。这些算法是基于鲁棒自适应控制理论的【4】。他们的变量学习增益比传统的反向传播算法学习的更快，这里的缺陷解决使用权重估计有界性。然而，这些算法对噪声敏感，因为每一次的学习方向是通过一个时间步的教学数据选择的。
本文中，提出一个新颖的学习算法，使用几个时间步的学习数据决定每个权重的一个学习增益。这样，学习的方向会更有效，收敛加权
估计到最优的条件就比较放松。
我们还简要的证明权重的有界性，并考虑学习数据大小和学习效率之间的关系。此外，简单的数值模拟表明算法的效率。
2、问题的设定
在图1中，显示三层神经网络。问题如何使用这个神经网络近似未知有界非线性函数y=f（x）。
假设如下：
- 输入x是有界的，并且函数f（x）的一个上界是已知的。
- 众所周知，用以足够精度的估计函数f（x）的神经元数量是必要的。
- 有一个有限的最优权重。、
我们定义一些符号：
。。。。。。。
图1中神经网络的输出由下面公式给出：
在这个形态下，神经网络似乎不是一个能够近似一般有界非线性功能的。然而，函数f（x）的上界从假设里已知，所以我们可以归一化教学信号从0到1.因此，由公式1决定的神经网络可以近似所有有界非线性函数。
时刻i的一个参数向量由下面公式给出：
把 看做参数向量的优化，参数误差向量有下面的形式给出：
神经网络输出误差有下面给出：
公式4得出:
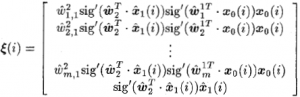
是建模误差的和，是泰勒展开式的余项。
收集余下t0步的误差数据，得到
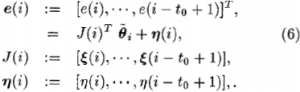
然后把公式6作为一个线性系统，通过最小二乘法得到
这就是众所周知的非线性最小二乘法：GN算法。然而，不能保证矩阵 
对于任意的t0和输入信号x（i）是满秩的。基于此，替换矩阵 为矩阵 
， 
，则学习算法变为：
这就是改进的GN算法，称为LM算法【3】。增加 
修正术语【4】到LM算法，我们有下面的学习算法：
接下来，我们引入一个正定对称矩阵权衡数据：
为了简化符号，我们提出e（i）， 
为 . 
此外，引入一个标量（无向量）增益 
，学习算法变为
公式10中，标量增益 必须满足下面的条件，保证参数收敛条件和有界性：
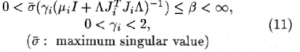
下面章节证明通过公式10决定的学习算法参数估计的有界性。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
