转载

数据结构基础温故-2.栈

现实生活中的事情往往都能总结归纳成一定的数据结构，例如餐馆中餐盘的堆叠和使用，羽毛球筒里装的羽毛球等都是典型的栈结构。而在.NET中，值类型在线程栈上进行分配，引用类型在托管堆上进行分配，本文所说的“栈”正是这种数据结构。栈和队列都是常用的数据结构，它们的逻辑结构与线性表相通，不同之处则在于操作受某种特殊限制。因此，栈和队列也被称为操作受限的线性表。这里，我们首先来了解一下栈。

一、栈的概念及操作

1.1 栈的基本特征

数据结构基础温故-2.栈

栈（stack）是限定仅在表尾进行插入和删除操作的线性表。其特点是：” 后进先出 “或” 先进后出 “。

1.2 栈的基本操作

（1）栈的插入操作，叫作进栈，也称压栈、入栈：

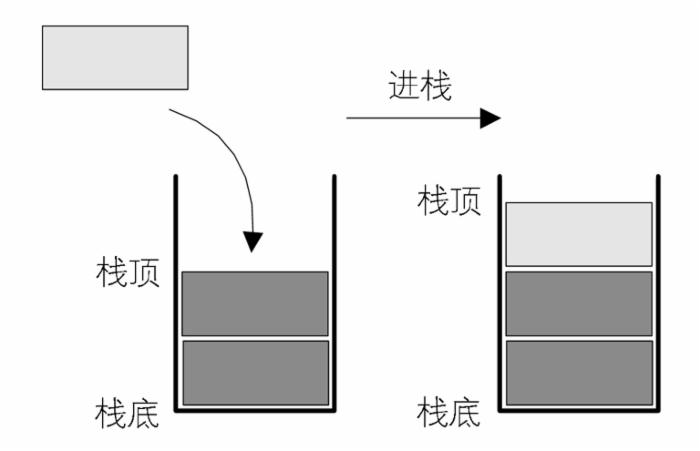
数据结构基础温故-2.栈

（2）栈的删除操作，叫作出栈，也有的叫作弹栈：

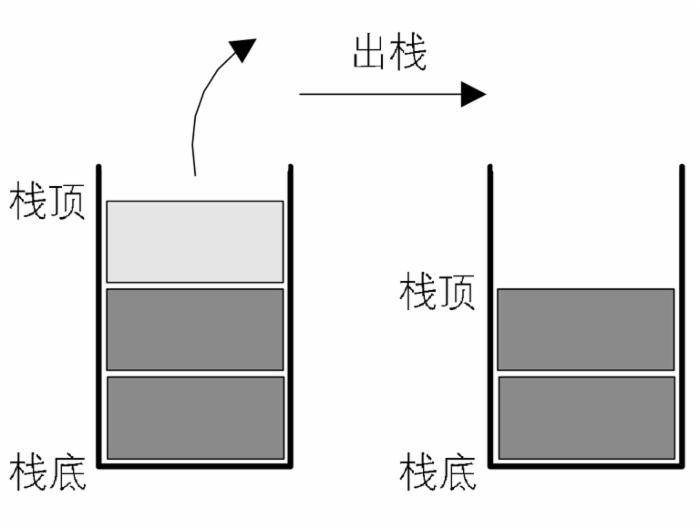
数据结构基础温故-2.栈

二、栈的基本实现

既然栈属于特殊的线性表，那么其实现也会有两种形式：顺序存储结构和链式存储结构。首先，对于Stack，我们希望能够提供以下几个方法供调用：

Stack<T>()	创建一个空的栈
void Push(T s)	往栈中添加一个新的元素
T Pop()	移除并返回最近添加的元素
bool IsEmpty()	栈是否为空
int Size()	栈中元素的个数

2.1 栈的顺序存储实现

对于顺序存储，我们可以参照顺序表的实现方式，借助数组来存储各个数据元素，然后对这个数组进行一定的封装，提供指定的操作对数据元素进行插入和删除即可。

（1）入栈操作实现

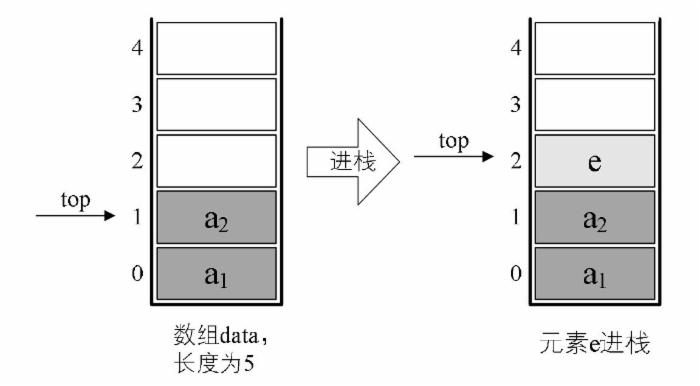
数据结构基础温故-2.栈

/// <summary> /// 入栈 /// </summary> /// <param name="node">节点元素</param> public void Push(T node) {  if (index == nodes.Length)  {   // 增大数组容量   ResizeCapacity(nodes.Length * 2);  }  nodes[index] = node;  index++; }

借助数组来实现入栈操作，其关键之处就在于top指针的移动。这里index初始值为0，每次入栈一个则将index加1，即指向下一个即将入栈的位置。由于这里采用了动态扩容的机制，所以没有判断栈中元素个数是否达到了最大值。

（2）出栈操作实现

出栈操作需要先去的要出栈的元素，然后将index减1，即指向下一个即将出栈的元素的位置。

/// <summary> /// 出栈 /// </summary> /// <returns>出栈节点元素</returns> public T Pop() {  if(index == 0)  {   return default(T);  }  T node = nodes[index - 1];  index--;  nodes[index] = default(T);  if (index > 0 && index == nodes.Length / 4)  {   // 缩小数组容量   ResizeCapacity(nodes.Length / 2);  }  return node; }

这里首先需要判断index是否已经到达了最小值，出栈的元素位置需要置为默认值（如果是int数组，那么会重置为0），最后返回出栈的元素对象。这里当元素个数小于数组的四分之一时会进行容量收缩操作。

（3）完整的类实现

/// <summary> /// 基于数组的栈实现 /// </summary> /// <typeparam name="T">类型</typeparam> public class MyArrayStack<T> {  private T[] nodes;  private int index;  public MyArrayStack(int capacity)  {   this.nodes = new T[capacity];   this.index = 0;  }  /// <summary>  /// 入栈  /// </summary>  /// <param name="node">节点元素</param>  public void Push(T node)  {   if (index == nodes.Length)   {    // 增大数组容量    ResizeCapacity(nodes.Length * 2);   }   nodes[index] = node;   index++;  }  /// <summary>  /// 出栈  /// </summary>  /// <returns>出栈节点元素</returns>  public T Pop()  {   if(index == 0)   {    return default(T);   }   T node = nodes[index - 1];   index--;   nodes[index] = default(T);   if (index > 0 && index == nodes.Length / 4)   {    // 缩小数组容量    ResizeCapacity(nodes.Length / 2);   }   return node;  }  /// <summary>  /// 重置数组大小  /// </summary>  /// <param name="newCapacity">新的容量</param>  private void ResizeCapacity(int newCapacity)  {   T[] newNodes = new T[newCapacity];   if(newCapacity > nodes.Length)   {    for (int i = 0; i < nodes.Length; i++)    {     newNodes[i] = nodes[i];    }   }   else   {    for (int i = 0; i < newCapacity; i++)    {     newNodes[i] = nodes[i];    }   }   nodes = newNodes;  }  /// <summary>  /// 栈是否为空  /// </summary>  /// <returns>true/false</returns>  public bool IsEmpty()  {   return this.index == 0;  }  /// <summary>  /// 栈中节点个数  /// </summary>  public int Size  {   get   {    return this.index;   }  } }

View Code

（4）简单的功能测试

首先，顺序入栈10个随机数，输出其元素个数与是否为空；然后依次出栈，输出每个数据元素；最后，再入栈15个随机数并出栈输出。

/// <summary> /// 基于数组的栈的测试 /// </summary> static void StackWithArrayTest() {  MyArrayStack<int> stack = new MyArrayStack<int>(10);  Console.WriteLine(stack.IsEmpty());  Random rand = new Random();  for (int i = 0; i < 10; i++)  {   stack.Push(rand.Next(1, 10));  }  Console.WriteLine("IsEmpty:{0}",stack.IsEmpty());  Console.WriteLine("Size:{0}", stack.Size);  Console.WriteLine("-------------------------------");  for (int i = 0; i < 10; i++)  {   int node = stack.Pop();   Console.Write(node + " ");  }  Console.WriteLine();  Console.WriteLine("IsEmpty:{0}", stack.IsEmpty());  Console.WriteLine("Size:{0}", stack.Size);  Console.WriteLine("-------------------------------");  for (int i = 0; i < 15; i++)  {   stack.Push(rand.Next(1, 15));  }  for (int i = 0; i < 15; i++)  {   int node = stack.Pop();   Console.Write(node + " ");  }  Console.WriteLine(); }

运行结果如下所示：

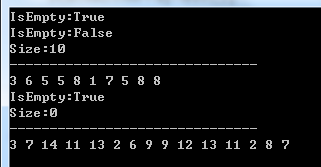
数据结构基础温故-2.栈

2.2 栈的链式存储实现

对栈的链式存储结构，我们可以参照单链表，为其设置一个头结点。这里，我们先来看看节点的定义：

（1）节点的定义实现

/// <summary> /// 基于链表的栈节点 /// </summary> /// <typeparam name="T"></typeparam> public class Node<T> {  public T Item { get; set; }  public Node<T> Next { get; set; }  public Node(T item)  {   this.Item = item;  }  public Node()  { } }

（2）入栈操作的实现

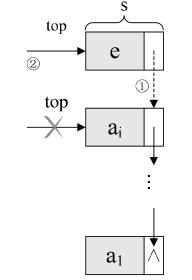
数据结构基础温故-2.栈

实现Push方法，即向栈顶压入一个元素，首先保存原先的位于栈顶的元素，然后新建一个新的栈顶元素，然后将该元素的下一个指向原先的栈顶元素。

/// <summary> /// 入栈 /// </summary> /// <param name="item">新节点</param> public void Push(T item) {  Node<T> oldNode = first;  first = new Node<T>();  first.Item = item;  first.Next = oldNode;  index++;  }

（3）出栈操作的实现

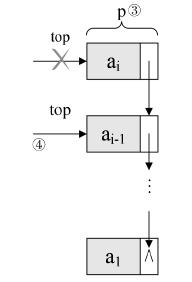
数据结构基础温故-2.栈

实现Pop方法，首先保存栈顶元素的值，然后将栈顶元素设置为下一个元素：

/// <summary>     /// 出栈     /// </summary>     /// <returns>出栈元素</returns>     public T Pop()     {         T item = first.Item;         first = first.Next;         index--;          return item;     }

这里还可以考虑将出栈元素的实例对象进行释放资源操作。

（4）完整的代码实现

/// <summary> /// 基于链表的栈节点 /// </summary> /// <typeparam name="T">元素类型</typeparam> public class Node<T> {  public T Item { get; set; }  public Node<T> Next { get; set; }  public Node(T item)  {   this.Item = item;  }  public Node()  { } } /// <summary> /// 基于链表的栈实现 /// </summary> /// <typeparam name="T">类型</typeparam> public class MyLinkStack<T> {  private Node<T> first;  private int index;  public MyLinkStack()  {   this.first = null;   this.index = 0;  }  /// <summary>  /// 入栈  /// </summary>  /// <param name="item">新节点</param>  public void Push(T item)  {   Node<T> oldNode = first;   first = new Node<T>();   first.Item = item;   first.Next = oldNode;   index++;  }  /// <summary>  /// 出栈  /// </summary>  /// <returns>出栈元素</returns>  public T Pop()  {   T item = first.Item;   first = first.Next;   index--;   return item;  }  /// <summary>  /// 是否为空栈  /// </summary>  /// <returns>true/false</returns>  public bool IsEmpty()  {   return this.index == 0;  }  /// <summary>  /// 栈中节点个数  /// </summary>  public int Size  {   get   {    return this.index;   }  } }

View Code

（5）简单的功能测试

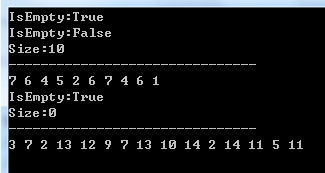
这里跟顺序存储结构的测试代码一致，就不再贴出来，直接看运行结果吧：

数据结构基础温故-2.栈

三、栈的基本应用

栈的应用场景很多，最常见的莫过于递归操作了，另外在运算表达式的求值上也有应用。这里看一个最经典的应用场景，进制转换问题。讲一个非负的十进制整数N转换成其他D进制数是计算机计算的一个基本问题，如(135)10进制=(207)8进制。最简单的解决办法就是连续取模%和整除/，例如将10进制的50转换为2进制数的过程如下图所示：

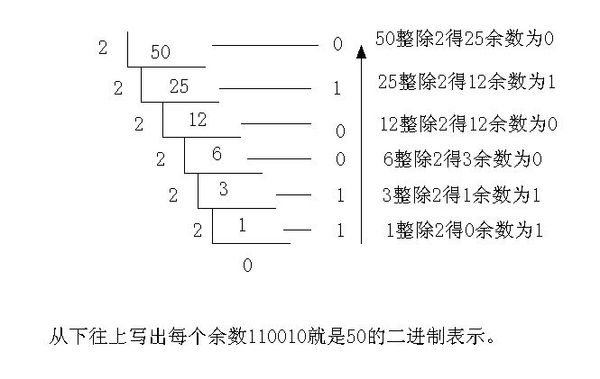
数据结构基础温故-2.栈

由上图的计算过程可知，D进制各位数的产生顺序是从低位到高位，而输出顺序却是从高位到低位，刚好和计算过程是相反的，因此可以利用栈进行逆序输出。

private static string DecConvert(int num, int dec) {  if (dec < 2 || dec > 16)  {   throw new ArgumentOutOfRangeException("dec", "只支持将十进制数转换为二进制到十六进制数");  }  MyLinkStack<char> stack = new MyLinkStack<char>();  int residue;  // 余数入栈  while (num != 0)  {   residue = num % dec;   if (residue >= 10)   {    // 如果是转换为16进制且余数大于10则需要转换为ABCDEF    residue = residue + 55;   }   else   {    // 转换为ASCII码中的数字型字符1~9    residue = residue + 48;   }   stack.Push((char)residue);   num = num / dec;  }  // 反序出栈  string result = string.Empty;  while (stack.Size > 0)  {   result += stack.Pop();  }  return result; }

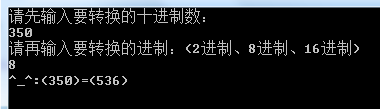
这里考虑到输出，所以使用了char类型作为节点数据类型，因此需要考虑ASCII码中的数字型字符与字母型字符。运行结果如下图所示：

①10进制数：350=>8进制数：536

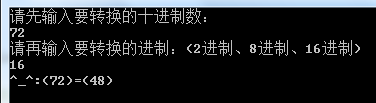
数据结构基础温故-2.栈

②10进制数：72=>16进制数：48

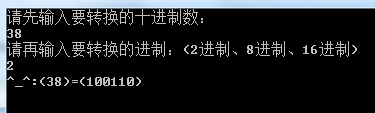
数据结构基础温故-2.栈

③10进制数：38=>2进制数：100110

数据结构基础温故-2.栈

四、.NET中的Stack<T>

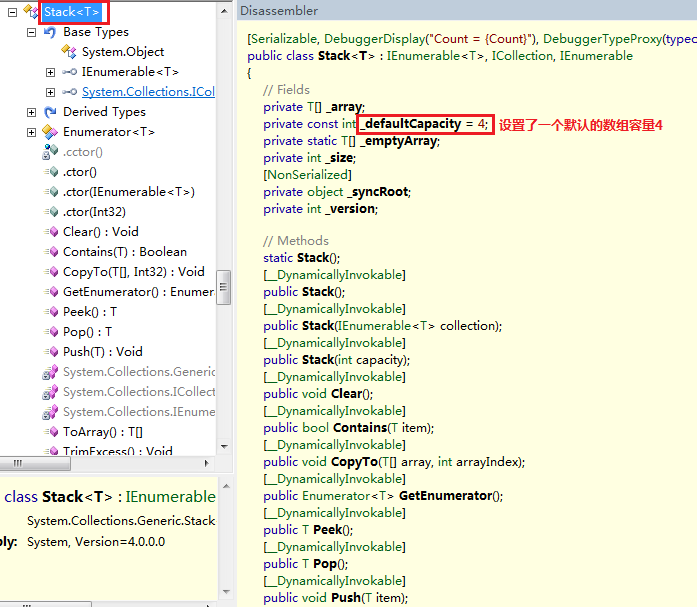
在.NET中，微软已经为我们提供了一个强大的栈类型：Stack<T>，这里我们使用Reflector工具查看其具体实现，具体看看Push和Pop两个方法，其他的各位园友可以自己去查看。

数据结构基础温故-2.栈

（1）Push方法源码

public void Push(T item) {  if (this._size == this._array.Length)  {   T[] destinationArray = new T[(this._array.Length == 0) ? 4 : (2 * this._array.Length)];   Array.Copy(this._array, 0, destinationArray, 0, this._size);   this._array = destinationArray;  }  this._array[this._size++] = item;  this._version++; }

（2）Pop方法源码

public T Pop() {  if (this._size == 0)  {   ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EmptyStack);  }  this._version++;  T local = this._array[--this._size];  this._array[this._size] = default(T);  return local; }